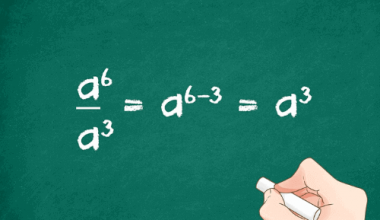O estudo dos lugares geométricos é fundamental para compreender como diferentes condições podem gerar curvas específicas no plano, como as circunferências. Esse conceito explora o conjunto de pontos a partir dos quais um segmento é visto sob um mesmo ângulo.
Nesse sentido, une conceitos de geometria plana com propriedades das circunferências e dos ângulos inscritos. Logo, permite resolver problemas que envolvem construção de figuras, análise de ângulos e identificação de simetrias.
Neste texto, você vai entender o que é o arco capaz e como é sua construção geométrica, além de revisar conceitos fundamentais e explorar casos especiais e aplicações. Acompanhe abaixo.
Navegue pelo conteúdo
Lugares geométricos e ângulos na circunferência
Lugar geométrico é o conjunto de todos os pontos do plano que satisfazem uma determinada propriedade. Como exemplo disso temos o conceito de circunferência, que é o lugar geométrico dos pontos que estão a uma distância fixa (o raio) de um ponto dado (o centro).
Alguns conceitos importantes envolvendo circunferências são:
- Ângulo central: tem vértice no centro da circunferência e seus lados são dois raios. A medida do ângulo central é igual à medida do arco que ele subtende (α = BC).

- Ângulo inscrito: tem vértice sobre a circunferência e seus lados são cordas que interceptam um arco. A medida de um ângulo inscrito é metade da medida do arco que ele subtende (β = BC/2) .

Obs.: Uma propriedade importante dos ângulos inscritos é:
- Todos os ângulos inscritos que subtendem o mesmo arco de uma circunferência são congruentes.
Definição de arco capaz
Dado um segmento AB e um ângulo fixo α, chamamos de arco capaz o lugar geométrico dos pontos P, no plano (mas não sobre a reta AB), tais que o ângulo ∠APB=α.
Em outras palavras, é o conjunto de todos os pontos P de onde conseguimos observar o segmento AB sob o mesmo ângulo α. O conjunto desses pontos forma uma curva com uma propriedade especial: é parte de uma circunferência.

A propriedade dos ângulos inscritos explica o fato de ao fixar um segmento AB e escolher um ponto P sobre a circunferência que passa por A, B e P, o ângulo ∠APB ser sempre o mesmo.
Assim, todos os pontos P que mantêm ∠APB=α estão sobre a mesma circunferência e o trecho dessa circunferência que corresponde a esses pontos é o arco capaz de AB para o ângulo α.
Construção do arco capaz
A construção do arco capaz pode ser feita de duas formas principais:
Método 1: construção geométrica elaborada
- Desenhe o segmento AB;

- Construa um ângulo ∠XAB=α, com lado AB;
- A partir de A, desenhe uma reta com ângulo α em relação a AB;

- Construa a mediatriz de AB;

- O ponto de interseção da mediatriz com a reta perpendicular ao lado auxiliar do ângulo ∠XAB no ponto A será o centro da circunferência do arco capaz; e

- Com centro nesse ponto e raio até A ou B, desenhe a circunferência.

Método 2: construção direta via triângulo
- Desenhe o segmento AB;

- Escolha um ponto P de forma que ∠APB=α; e

- Trace a circunferência que passa por A, B e P que é a circunferência do arco capaz.

O centro dessa circunferência estará na mediatriz do segmento AB, pois ela é perpendicular à AB e passa pelo seu ponto médio, propriedade comum a todas as circunferências que passam por dois pontos fixos.
+ Veja também: Lugares geométricos: definição, exemplos e questões
Dois arcos capazes para o mesmo ângulo
Um fato interessante é a existência de dois arcos capazes distintos para o mesmo ângulo α, localizados em lados opostos da reta AB. Ou seja, para um mesmo segmento e ângulo, é possível traçar duas circunferências diferentes, com arcos capazes complementares.

Arcos Capazes de α e 180° − α
Para um segmento AB, o arco capaz de um ângulo α e o do ângulo 180°−α aparecem de lados opostos da reta AB. Esse fenômeno está ligado à propriedade dos quadriláteros inscritíveis.
Essa propriedade revela que em um quadrilátero inscrito em uma circunferência, a soma dos ângulos opostos é 180°. Assim, se em um lado do segmento temos um ponto P com ∠APB=α, então do outro lado existirá um ponto Q com ∠AQB=180°−α.

Casos Especiais
Arco Capaz de 90°:
Quando α=90° o arco capaz forma um semicírculo com diâmetro AB. Essa situação está relacionada ao Teorema de Tales: “Todo triângulo inscrito em uma semicircunferência com o lado AB como diâmetro é um triângulo retângulo.”
Arco Capaz de 180°:
O lugar geométrico é o próprio segmento AB, mas exclui os extremos A e B. Isso porque o ângulo ∠APB seria um ângulo raso (linha reta).
Arco Capaz de 0°:
Nesse caso, o lugar geométrico corresponde à reta AB, novamente sem os pontos A e B, pois de qualquer ponto dessa reta não é possível formar um ângulo entre A e B.
Resolução de problemas envolvendo arco capaz e principais erros
No Enem ou em outros vestibulares os problemas, em geral, aparecem envolvendo os seguintes pontos:
- A determinação do lugar geométrico de pontos a partir dos quais um segmento é visto sob um certo ângulo;
- A construção de triângulos com um lado fixo e um ângulo oposto dado;
- A prova de congruência de ângulos usando a propriedade do arco capaz;
- A comprovação de colinearidade de pontos, quando se deseja mostrar que um ponto não pertence ao arco capaz; e
- A combinação do arco capaz com propriedades de quadriláteros inscritíveis, teoremas de ângulos inscritos, ou mediatrizes.
Um dos principais erros dos estudantes é não compreender bem o conceito de lugar geométrico, o que compromete a interpretação da questão. Também é frequente confundir o ângulo capaz com outro ângulo, levando a construções ou fórmulas inadequadas.
O estudante pode, ainda, esquecer que existem dois arcos capazes para o mesmo ângulo sobre um segmento, o que pode gerar falhas na análise da figura. Além disso, muitos têm dificuldade na construção do centro e do raio da circunferência, especialmente ao usar mediatrizes e perpendiculares com precisão.
Questão do vestibular envolvendo arco capaz
Enem (2023)
Num certo momento de um jogo digital, a tela apresenta a imagem representada na figura. O ponto Q₁ representa a posição de um jogador que está com a bola, os pontos Q₂, Q₃, Q₄, Q₅ e Q₆ também indicam posições de jogadores da mesma equipe, e os pontos A e B indicam os dois pés da trave mais próxima deles. No momento da partida retratado, o jogador Q₁ tem a posse da bola, que será passada para um dos outros jogadores das posições Qₙ, n ∈ {2, 3, 4, 5, 6}, cujo ângulo tenha a mesma medida do ângulo

Qual é o jogador que receberá a bola?
A) Q₂
B) Q₃
C) Q₄
D) Q₅
E) Q₆
Alternativa correta:
B
Perceba que o segmento é comum à todas as circunferências e estas são arcos capazes em relação à
.
O ângulo é um ângulo inscrito na circunferência que passa por Q₁.
Qualquer ângulo inscrito a essa mesma circunferência temos a mesma corda como referência será igual a α.
Como Q₃ está na mesma circunferência de Q₁, então
Portanto, o jogador Q₃ receberá a bola.
Prepare-se para o vestibular com o Estratégia!
Nos cursos preparatórios da Coruja, os alunos são treinados para conectar diferentes áreas do conhecimento e aplicar essas informações em simulados e provas.
As aulas são ministradas por professores especialistas, com nossos Livros Digitais Interativos (LDI), além de contar com simulados exclusivos. Clique no banner e comece seus estudos com o Estratégia Vestibulares!