Como resolver as questões de Física da 2ª Fase da Fuvest 2020

Fala, pessoal. Tudo certo? Sou o prof. Lucas Costa, professor de Física do Estratégia Vestibulares. Hoje, vamos resolver as questões de Física da prova da 2ª Fase do Vestibular da Fuvest 2020.

Navegue pelo conteúdo

Questão 01

Uma pessoa produz oscilações periódicas em uma longa corda formada por duas porções de materiais diferentes 1 e 2, nos quais a velocidade de propagação das ondas é, respectivamente, de 5 m/s e 4 m/s. Segurando a extremidade feita do material 1, a pessoa abaixa e levanta sua mão regularmente, completando um ciclo a cada 0,5 s, de modo que as ondas propagam‐se do material 1 para o material 2, conforme mostrado na figura. Despreze eventuais efeitos de reflexão das ondas.

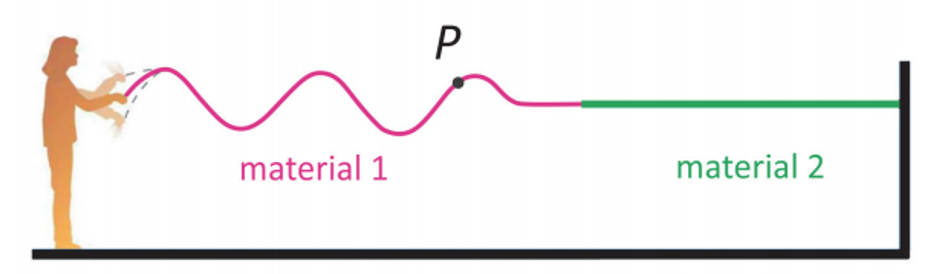
a) Circule, dentre os vetores na folha de respostas, aquele que melhor representa a velocidade do ponto P da corda no instante mostrado na figura.

b) Calcule a frequência e o comprimento de onda no material 1.

c) Calcule a frequência e o comprimento de onda no material 2.

Gabarito

a) Vertical e para baixo.

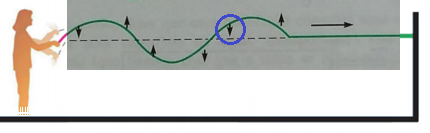
b) $\large \mathbit{f}=\mathbf{2}\ \mathbit{Hz}\ e\ \mathbit{\lambda}_\mathbf{1}=\mathbf{2},\mathbf{5}\ \mathbit{m}$

A frequência é dada pelo inverso do período, que é o tempo que a pessoa leva para completar um ciclo.

$\large f=\frac{1}{T}=\frac{1}{0,5}=2\ Hz$

Podemos usar a equação fundamental da ondulatória para determinarmos o comprimento de onda na corda feita com o material 1:

$\large v=\lambda\cdot f\Rightarrow\lambda=\frac{v}{f}$

$\large \lambda_1=\frac{5}{2}=2,5\ m$

c) $\large \mathbit{f}=\mathbf{2}\ \mathbit{Hz}\ e\ \mathbit{\lambda}_\mathbf{2}=\mathbf{2}\ \mathbit{m}$

A frequência depende somente da fonte emissora. Como a pessoa é a mesma, e o tempo que ela leva para completar cada ciclo também, a frequência da onda no material 2 também vale 2 Hz.

Podemos calcular o comprimento de onda de maneira análoga:

$\large \lambda_2=\frac{4}{2}=2\ m$

Questão 02

Um mol de um gás ideal monoatômico é resfriado adiabaticamente de uma temperatura inicial T₁ até uma temperatura final T₁/3.

Com base nessas informações, responda:

a) O gás sofreu expansão ou compressão ao final do processo? Justifique sua resposta.

b) Encontre o valor do trabalho realizado pelo gás nesse processo em termos da constante universal dos gases ideais R e de T₁.

c) Encontre a razão entre as pressões final e inicial do gás após o processo.
Note e adote:

Em um processo adiabático, não há troca de calor com o ambiente.
Energia interna por mol de um gás ideal monoatômico: $\large U=3RT/2$ .

Para o processo adiabático em questão, vale a relação $\large PV^{5/3}=constante$ .

Gabarito

a) Em uma transformação adiabática, vale a Lei de Poisson-Laplace:

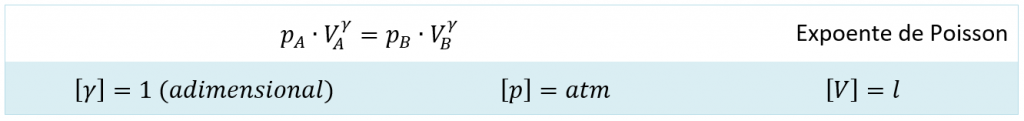
Esse tipo de transformação normalmente é observada uma curva que vai de uma isoterma a outra.

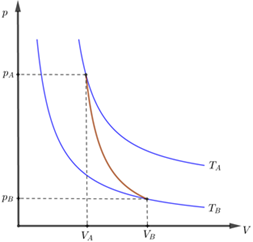
Figura 07.8 – Uma expansão adiabática de um gás. Note que VB > VA.

Isso significa que a pressão, o volume e a temperatura do gás variam. Em uma contração adiabática ocorre diminuição do volume, aumento de pressão e aumento de temperatura, por outro lado, em uma expansão adiabática o volume aumenta, e a pressão e a temperatura diminuem.

A questão pede que demonstremos:

$\large p_1\cdot V_1^\gamma=p_2\cdot V_2^\gamma$

Devemos substituir a pressão por sua relação com a equação de Clapeyron

$\large p\cdot V=n\cdot R\cdot T\Rightarrow p=\ \frac{n\cdot R\cdot T}{V}$

Fazendo a substituição na expressão anterior, temos:

$\large p_1\cdot V_1^\gamma=p_2\cdot V_2^\gamma$

$\large \frac{n\cdot R\cdot T_1}{V_1}\cdot V_1^\gamma=\frac{n\cdot R\cdot T_2}{V_2}\cdot V_2^\gamma$

$\large \frac{\cancel n \cdot \cancel R \cdot T_{1}}{V_{1}}\cdot V_{1}^{\gamma }=\frac{\cancel n \cdot \cancel R \cdot T_{2}}{V_{2}}\cdot V_{2}^{\gamma }$

$\large \frac{T_1}{V_1}\cdot V_1^\gamma=\frac{T_2}{V_2}\cdot V_2^\gamma$

$\large T_1\cdot V_1^{\gamma-1}=T_2\cdot V_2^{\gamma-1}$

$\large T_1\cdot V_1^{\gamma-1}=\frac{T_1}{3}\cdot V_2^{\gamma-1}$

$\large 3\cdot V_1^{\gamma-1}=V_2^{\gamma-1}$

Pelo “Note e adote” devemos perceber que $\large \gamma=5/3$ , logo $\large \gamma-1=2/3$ :

$\large V_2=V_1\cdot3^{\left(\frac{1}{\gamma-1}\right)}=V_1\cdot3^{\left(\frac{3}{2}\right)}$

$\large V_2=\sqrt{27}\cdot V_1$

Como $\large ∆U=Q-W$

Como se trata de uma transformação adiabática, Q=0, daí:

$\large \Delta U=-W\Rightarrow W=-\Delta U$

Pela expressão fornecida no “Note e adote”:

$\large W=\frac{-3\cdot R\cdot \Delta T}{2}=\frac{3\cdot R\cdot -\Delta T}{2}=\frac{3\cdot R\cdot\left(T_1-T_1/3\right)}{2}$

$\large W=\frac{3\cdot R\cdot\frac{2}{3}\cdot T_1}{2}=R\cdot T_1$

c) Devemos usar novamente a relação para uma transformação adiabática:

$\large p_1\cdot V_1^\gamma=p_2\cdot V_2^\gamma$

$\large p_i\cdot V_1^{5/3}=p_f\cdot V_2^{5/3}$

$\large p_i\cdot V_1^{\frac{5}{3}}=p_f\cdot\left(3^\frac{3}{2}\cdot V_1\right)^\frac{5}{3}$

$\large p_i\cdot V_1^{\frac{5}{3}}=p_f\cdot 3^\frac{5}{2}\cdot V_1^{\frac{5}{3}}$

$\large p_f=\frac{p_i}{3^\frac{5}{2}}$

Questão 03

A tomografia por emissão de pósitrons (PET) é uma técnica de imagem por contraste na qual se utilizam marcadores com radionuclídeos emissores de pósitrons. O radionuclídeo mais utilizado em PET é o isótopo 18 do flúor, que decai para um núcleo de oxigênio‐18, emitindo um pósitron. O número de isótopos de flúor‐18 decai de forma exponencial, com um tempo de meia‐vida de aproximadamente 110 minutos.

A imagem obtida pela técnica de PET é decorrente da detecção de dois fótons emitidos em sentidos opostos devido à aniquilação, por um elétron, do pósitron resultante do decaimento. A detecção é feita por um conjunto de detectores montados num arranjo radial. Ao colidir com um dos detectores, o fóton gera cargas no material do detector, as quais, por sua vez, resultam em um sinal elétrico registrado no computador do equipamento de tomografia. A intensidade do sinal é proporcional ao número de núcleos de flúor‐18 existentes no início do processo.

a) Após a realização de uma imagem PET, o médico percebeu um problema no funcionamento do equipamento e o reparo durou 3h40min. Calcule a razão entre a intensidade do sinal da imagem obtida após o reparo do equipamento e a da primeira imagem.

b) Calcule a energia de cada fóton gerado pelo processo de aniquilação elétron‐pósitron considerando que o pósitron e o elétron estejam praticamente em repouso. Esta é a energia mínima possível para esse fóton.

c) A carga elétrica gerada dentro do material do detector pela absorção do fóton é proporcional à energia desse fóton. Sabendo‐se que é necessária a energia de 3eV para gerar o equivalente à carga de um elétron no material, estime a carga total gerada quando um fóton de energia 600keV incide no detector.

Note e adote:

O elétron e o pósitron, sua antipartícula, possuem massas iguais e cargas de sinais opostos. Relação de Einstein para a energia de repouso de uma partícula: E = mc².

Carga do elétron $\large =1,6\cdot{10}^{-19}\ C$

Massa do elétron: $\large m=9\cdot{10}^{-31}\ kg$

Velocidade da luz: $\large c=3\cdot{10}^8\ m/s$

$\large 1\ eV=1,6\cdot{10}^{-19}\ J$

“Tempo de meia‐vida”: tempo necessário para que o número de núcleos radioativos caia para metade do valor inicial.

Gabarito

a) Como o texto diz que “A intensidade do sinal é proporcional ao número de núcleos de flúor‐18 existentes no início do processo”, podemos relacionar a intensidade com o que sobrou, após a degradação dos núcleos radioativos. Podemos relacionar essa quantidade com o tempo de meia-vida:

$\large N=\frac{N_0}{2^n}$

O número de meias-vidas n pode ser calculado pela razão entre o tempo total decorrido e o tempo de meia-vida, desde que esses estejam em uma mesma unidade de tempo:

$\large n=\frac{t}{\frac{t_1}{2}}=\frac{3h\ 40\ min}{110\ min}=\frac{220\ min}{110\ min}=2$

Voltando à expressão anterior:

$\large N=\frac{N_0}{2^n}=\frac{N_0}{2^2}=\frac{N_0}{4}$

Isso nos permite concluir que a razão pedida vale 1/4.

b) Devemos usar a equação de Einstein fornecida no “Note e adote”, com o cuidado de nos lembrar que se trata de duas partículas envolvidas na aniquilação: o elétron e o pósitron e que são formados dois fótons:

$\large E=m\cdot c^2$

$\large 2\cdot E=\left(2\cdot9\cdot{10}^{-31}\right)\cdot\left(3\cdot{10}^8\right)^2$

$\large E=9\cdot{10}^{-31}\cdot9\cdot{10}^{16}$

$\large E=81\cdot{10}^{-15}=8,1\cdot{10}^{-14}\ J$

c) O enunciado diz que “A carga elétrica gerada dentro do material do detector pela absorção do fóton é proporcional à energia desse fóton”. Devemos relacionar os dados fornecidos no enunciado:

$\large 3\ eV \ \ \ \ ---------- \ \ \ \ 1\ qe \\ \\ 600\cdot 10^{3}\ eV \ \ \ \ ---------- \ \ \ \ q$

Como as grandezas são diretamente proporcionais, podemos efetuar a multiplicação cruzada dos valores:

$\large 3\cdot q=1\cdot 600\cdot{10}^3$

$\large q=200\cdot{10}^3=2\cdot{10}^5\ qe$

Devemos substituir a carga do elétron para determinarmos a carga em coulomb:

$\large q=2\cdot{10}^5\cdot1,6\cdot{10}^{-19}=3,2\cdot{10}^{-14}\ C$

Questão 04

Em um ambiente do qual se retirou praticamente todo o ar, as placas de um capacitor estão arranjadas paralelamente e carregadas com cargas de mesma magnitude Q e sinais contrários, produzindo, na região entre as placas, um campo elétrico que pode ser considerado uniforme, com módulo igual a $\large {10}^6\ V/m$ . Uma partícula carregada negativamente, com carga de módulo igual a $\large {10}^{-9}\ C$ , é lançada com velocidade de módulo $\large V_0$ igual a $\large 100\ m/s$ ao longo da linha que passa exatamente pelo centro da região entre as placas, como mostrado na figura. A distância d entre as placas é igual a $\large 1\ mm$ . Despreze os efeitos gravitacionais.

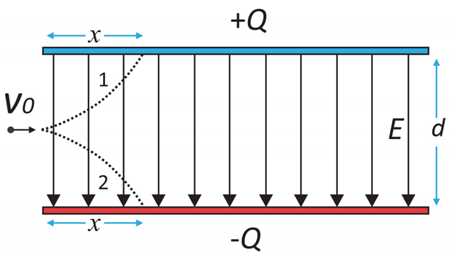
a) Aponte, entre as trajetórias 1 e 2 mostradas na figura, aquela que mais se aproxima do movimento da partícula na região entre as placas.

b) Sabendo que a massa da partícula é igual a $\large 10\ \mu g$ , determine a que distância horizontal x a partícula atingirá uma das placas, supondo que elas sejam suficientemente longas.

c) Quais seriam o sentido e o módulo de um eventual campo magnético a ser aplicado na região entre as placas, perpendicularmente ao plano da página, para que a partícula, em vez de seguir uma trajetória curva, permaneça movendo‐se na mesma direção e no mesmo sentido com que foi lançada?

Gabarito

a) Como a carga é negativa, temos que a força elétrica será vertical e para cima, fazendo com que a partícula descreva a trajetória 1. Devemos nos lembrar que o enunciado fala para desconsiderarmos efeitos gravitacionais, ou seja, devemos desconsiderar a ação da força peso.

b) Devemos calcular a aceleração vertical, sabendo que a força resultante é a força elétrica:

$\large F_r=m\cdot a$

$\large F_{el}=m\cdot a_y\Rightarrow a_y=\frac{q\cdot E}{m}$

$\large a_y=\frac{{10}^{-9}\cdot{10}^6}{10\cdot{10}^{-6}\cdot{10}^{-3}}=\frac{{10}^{-3}}{{10}^{-8}}={10}^5\ m/s^2$

Podemos calcular o tempo para que a partícula chegue até a placa positiva do capacitor usando a equação da posição para o MRUV. Note que a velocidade vertical inicial é nula e que a distância a ser percorrida é a metade da distância entre as placas:

$\large \Delta S_y=v_0\cdot t+\frac{a\cdot t^2}{2}$

$\large \frac{1\cdot{10}^{-3}}{2}=\frac{{10}^5\cdot t^2}{2}$

$\large t^2={10}^{-8}\Rightarrow t={10}^{-4}\ s$

Sabemos que o deslocamento horizontal é uniforme. De posse do tempo, podemos calcular a distância horizontal percorrida:

$\large \Delta _{x}=v_x\cdot t=100\cdot{10}^{-4}={10}^{-2}\ m=1\ cm$

c) Para que a partícula permaneça movendo-se na mesma direção e sentido com que foi lançada, a resultante vertical das forças deve ser nula. Para que isso aconteça, a força magnética deverá ser vertical e para baixo.

Nessa hipótese, para a partícula carregada negativamente e com velocidade horizontal e para a direita, precisaremos do campo magnético entrando no plano do papel. Isso pode ser verificado pela regra da mão direita:

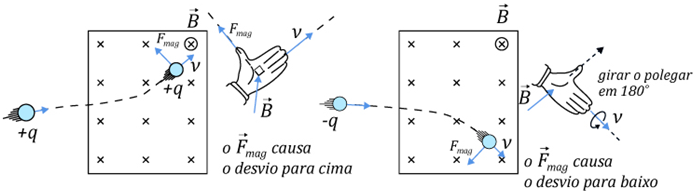
Podemos calcular o módulo do campo magnético igualando o módulo da força magnética ao módulo da força elétrica:

$\large F_{mag}=F_{el}$

$\large q\cdot v\cdot B=q\cdot E$

$\large B=\frac{E}{v}=\frac{{10}^6}{100}={10}^4\ T$

Questão 05

Em janeiro de 2019, a sonda chinesa $\large Chang'$ e 4 fez o primeiro pouso suave de um objeto terrestre no lado oculto da Lua, reavivando a discussão internacional sobre programas de exploração lunar.

Considere que a trajetória de uma sonda com destino à Lua passa por um ponto P, localizado a $\large 2/3\ d_{TL}$ do centro da Terra e a $\large 1/3\ d_{TL}$ do centro da Lua, sendo $\large d_{TL}$ a distância entre os centros da Terra e da Lua.

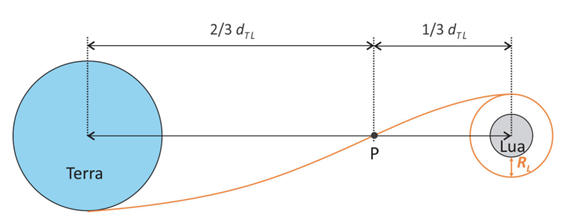
a) Considerando que a massa da Terra é cerca de 82 vezes maior que a massa da Lua, determine a razão $\large F_T/F_L$ entre os módulos da força gravitacional que a Terra e a Lua, respectivamente, exercem sobre a sonda no ponto P.

Ao chegar próximo à Lua, a sonda foi colocada em uma órbita lunar circular a uma altura igual ao raio da $\large Lua (R_L)$ , acima de sua superfície, como mostra a figura. Desprezando os efeitos da força gravitacional da Terra e de outros corpos celestes ao longo da órbita da sonda,

b) determine a velocidade orbital da sonda em torno da Lua em termos da constante gravitacional G, da massa da $\large Lua\ M_L$ e do raio da $\large Lua\ R_L$ ;

c) determine a variação da energia mecânica da nave quando a altura da órbita, em relação à superfície da Lua, é reduzida para $\large 0,5\ R_L$ . Expresse seu resultado em termos de G, R_L, M_L e da massa da sonda $\large m_S$ .

Note e adote:

O módulo da força gravitacional entre dois objetos de massas M e m separados por uma distância d é dado por $\large F=GMm/d^2$

A energia potencial gravitacional correspondente é dada por $\large U=-GMd/d$ .
Assuma a distância da Terra à Lua como sendo constante.

Gabarito

a) Podemos calcular a razão pedida usando a relação fornecida no “Note e adote”:

$\large \frac{F_T}{F_L}=\frac{\frac{G\cdot M_T\cdot m_S}{\left(\frac{2}{3}d_{TL}\right)^2}}{\frac{G\cdot M_L\cdot m_S}{\left(\frac{1}{3}d_{TL}\right)^2}}=\frac{\frac{G\cdot M_T\cdot m_S}{\frac{4}{9}\cdot\left(d_{TL}\right)^2}}{\frac{G\cdot M_L\cdot m_S}{\frac{1}{9}\cdot\left(d_{TL}\right)^2}}=\frac{\frac{G\cdot M_T\cdot m_S}{\frac{4}{9}\cdot\left(d_{TL}\right)^2}}{\frac{G\cdot M_L\cdot m_S}{\frac{1}{9}\cdot\left(d_{TL}\right)^2}}$

$\large \frac{F_T}{F_L}=\frac{\frac{M_T}{4}}{\frac{M_L}{1}}=\frac{\frac{M_T}{4}}{M_L}=\frac{M_T}{4\cdot M_L}$

Como a massa da Terra é 82 vezes maior que a massa da Lua:

$\large \frac{F_T}{F_L}=\frac{82\cdot M_L}{4\cdot M_L}=\frac{82\cdot M_L}{4\cdot M_L}=\frac{41}{2}$

b) Quando a sonda descreve uma trajetória circular em torno da Lua, temos que a força gravitacional atua como resultante centrípeta:

$\large F_{grav}=F_{cp}$

$\large \frac{G\cdot M_L\cdot m_S}{\left(2\cdot R_L\right)^2}=\frac{m_S\cdot v^2}{2\cdot R_L}$

$\large \frac{G\cdot M_L\cdot m_S}{4\cdot\left(R_L\right)^2}=\frac{m_S\cdot v^2}{{2\cdot R}_L}$

$\large v=\sqrt{\frac{G\cdot M_L}{2\cdot R_L}}$

c) E energia mecânica da nave é dada pela soma da energia potencial gravitacional e da energia cinética. Para a situação do satélite a uma distância $\large R_L$ da superfície da Lua:

$\large EM=Epot+Ec$

$\large EM_{R_L}=\frac{-G\cdot M_L\cdot m_S}{2\cdot R_L}+\frac{m_S\cdot v^2}{2}$

Podemos escrever a energia cinética em função dos elementos da alternativa anterior:

$\large \frac{m_S\cdot v^2}{2\cdot R_L}=\frac{G\cdot M_L\cdot m_S}{4\cdot\left(R_L\right)^2}$

$\large \frac{m_S\cdot v^2}{2}=\frac{G\cdot M_L\cdot m_S}{4\cdot R_L}$

Voltando à expressão anterior:

$\large EM_{R_L}=\frac{-G\cdot M_L\cdot m_S}{2\cdot R_L}+\frac{G\cdot M_L\cdot m_S}{4\cdot R_L}$

$\large EM_{R_L}=\frac{-2\cdot G\cdot M_L\cdot m_S}{4\cdot R_L}+\frac{G\cdot M_L\cdot m_S}{4\cdot R_L}$

$\large EM_{R_L}=\frac{-G\cdot M_L\cdot m_S}{4\cdot R_L}$

De maneira análoga, para a distância reduzida para $\large 0,5\ R_L$ :

$\large EM_{{0,5R}_L}=\frac{-G\cdot M_L\cdot m_S}{1,5\cdot R_L}+\frac{m_S\cdot v_{{0,5R}_L}^2}{2}$

E para o termo da cinética:

$\large \frac{m_S\cdot v^2}{{\frac{3}{2}R}_L}=\frac{G\cdot M_L\cdot m_S}{\left(\frac{3}{2}\cdot R_L\right)^2}$

$\large \frac{m_S\cdot v^2}{1}=\frac{G\cdot M_L\cdot m_S}{\frac{3}{2}\cdot R_L}$

$\large \frac{m_S\cdot v^2}{2}=\frac{G\cdot M_L\cdot m_S}{3\cdot R_L}$

Voltando:

$\large EM_{{0,5R}_L}=\frac{-G\cdot M_L\cdot m_S}{\frac{3}{2}\cdot R_L}+\frac{G\cdot M_L\cdot m_S}{3\cdot R_L}$

$\large EM_{{0,5R}_L}=-\frac{G\cdot M_L\cdot m_S}{3\cdot R_L}$

E a diferença será de:

$\large EM_{{0,5R}_L}-EM_{R_L}=-\frac{G\cdot M_L\cdot m_S}{3\cdot R_L}-\left(\frac{-G\cdot M_L\cdot m_S}{4\cdot R_L}\right)$

$\large EM_{R_L}-EM_{{0,5R}_L}=\frac{-G\cdot M_L\cdot m_S}{3\cdot R_L}+\frac{G\cdot M_L\cdot m_S}{4\cdot R_L}$

$\large EM_{R_L}-EM_{{0,5R}_L}=\frac{-4\cdot G\cdot M_L\cdot m_S}{12\cdot R_L}+\frac{3\cdot G\cdot M_L\cdot m_S}{12\cdot R_L}$

$\large EM_{R_L}-EM_{{0,5R}_L}=\frac{-G\cdot M_L\cdot m_S}{12\cdot R_L}$

Questão 06

$\large M=60\ kg$ Uma equilibrista de massa M desloca‐se sobre uma tábua uniforme de comprimento L e massa m apoiada (sem fixação) sobre duas colunas separadas por uma distância $\large D\ (D<l)$ de modo que o centro da tábua esteja equidistante das colunas. O ponto de apoio da equilibrista está a uma distância $\large d\ (tal\ que\ D/2<d<l/2)$ do centro da tábua, como mostra a figura.

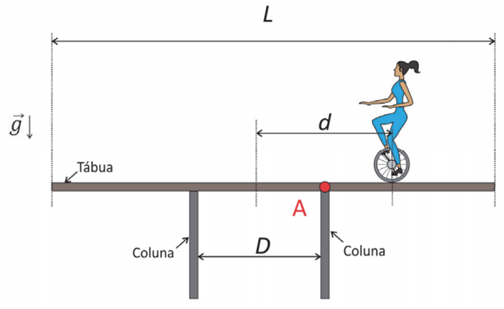
a) Considerando que a tábua está em equilíbrio, faça um diagrama indicando todas as forças que atuam sobre a tábua e seus respectivos pontos de aplicação.

b) Calcule o torque resultante exercido pelos pesos da equilibrista e da tábua em relação ao ponto A (ponto de apoio da tábua na coluna mais próxima da equilibrista). Escreva sua resposta em termos de grandezas mencionadas no enunciado (M, L, m, D, d) e da aceleração da gravidade g.

c) Calcule a distância máxima $\large d_{max}$ da equilibrista ao centro da tábua para que o conjunto permaneça em equilíbrio estático.
Considere os seguintes dados: comprimento da tábua: $\large L=5\ m$ ; massa da tábua: $\large m=20\ kg$ , massa da equilibrista: , distância entre as colunas: $\large D=3\ m$ .

Note e adote:

Despreze as espessuras da tábua e da coluna.

Use $\large g=10\ m/s^2$

Gabarito

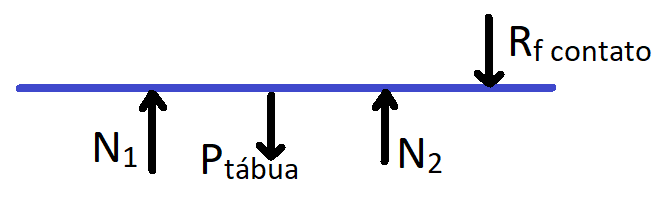
b) Devemos nos lembrar que a convenção adota torque no sentido anti-horário como positivo. Com isso, o torque gerado pela equilibrista será negativo e pelo peso da tábua positivo. O torque resultante será dado por:

$\large M_{res}=m\cdot g\cdot\frac{D}{2}-M\cdot g\cdot\left(d-\frac{D}{2}\right)$

c) Na situação da distância máxima, $\large N_1$ tenderá a zero:

$\large M_{res}=0$

$\large m\cdot g\cdot\frac{D}{2}=M\cdot g\cdot\left(d-\frac{D}{2}\right)$

$\large m\cdot\frac{D}{2}=M\cdot d-M\cdot\frac{D}{2}$

$\large M\cdot d=m\cdot\frac{D}{2}+M\cdot\frac{D}{2}$

$\large d=\frac{\left(m+M\right)\cdot D}{2\cdot M}$

$\large d=\frac{\left(20+60\right)\cdot3}{2\cdot60}=\frac{80\cdot3}{120}=\frac{240}{120}=2\ m$

Com isso, encerramos a nossa correção de Física da 2ª Fase da UNESP 2020. Se ficou alguma dúvida, pode entrar em contato comigo através do nosso Fórum de Dúvidas ou pelas minhas redes sociais. Vou deitar esta correção disponível para download. Você vai poder baixar de forma gratuita no link a seguir.

">Resolução FUVEST 2020 – 2ª Fase – Física" class="wp-block-file__button" download>Baixar

Abraços

Prof. Lucas Costa

Instagram: @prof.lucascosta

CURSOS PARA FUVEST

Como resolver as questões de Física da 2ª Fase da Fuvest 2020

Questão 01

Gabarito

Questão 02

Gabarito

Questão 03

Gabarito

Questão 04

Gabarito

Questão 05

Gabarito

Questão 06

Gabarito

Raquel Oshio

Resolução da prova de Matemática da 2ª Fase da Fuvest 2020

Gabarito FUVEST: baixe e assista à resolução da 2ª Fase

Campo elétrico: o que é, fórmulas e questões

Gravidade: o que é, valor e muito mais!

Gabarito UEL 2020 – Física – Resolução Comentada

Como resolver as questões de Física da 2ª Fase da Fuvest 2020

Questão 01

Gabarito

Questão 02

Gabarito

Questão 03

Gabarito

Questão 04

Gabarito

Questão 05

Gabarito

Questão 06

Gabarito

Raquel Oshio

Resolução da prova de Matemática da 2ª Fase da Fuvest 2020

Gabarito FUVEST: baixe e assista à resolução da 2ª Fase

Você pode gostar também