Gabarito Unesp 2020 - Física - Resolvido

Olá, caro aluno. Seja Bem-Vindo. Escrevo este artigo para disponibilizar a você a resolução das questões de Física da prova de 1ª fase UNESP 2020. Durante a leitura deste artigo, você vai conferir o que cobravam as questões e como você teria que resolver até chegar ao Gabarito sugerido pela UNESP. Vamos nessa?

">Prova UNESP 2020 – Física – Resolução" class="wp-block-file__button" download>Baixar

Prova UNESP 2020

Questão 50

Com o intuito de formar uma rede de observação e coleta de dados sobre as chuvas, um professor de geografia instalou, nas escolas em que trabalha, instrumentos meteorológicos para recolher e medir a quantidade de água precipitada. Após uma chuva, um aluno verificou que o instrumento registrou 40 ?? de água em um tubo, no formato de um cilindro reto com 20 ?? de diâmetro, conforme a figura.

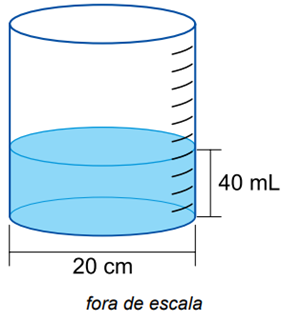
A partir dessas informações, o aluno deve comunicar ao professor que o valor aproximado indicado no

(A) pluviômetro foi 1,3 mm de chuva.

(B) higrômetro foi 1,3 mm de chuva.

(D) pluviômetro foi 2 mm de chuva.

(E) higrômetro foi 2 mm de chuva.

Resolução Comentada

De acordo com a figura, o raio da base do cilindro é de 10 cm (metade do diâmetro). O volume de água no cilindro é dado por:

$\large V=A_{base}\cdot altura$

Portanto, a altura de água no cilindro é igual a:

$\large 40ml=40cm^{3}=A_{base}\cdot h$

$\large 40cm^{3}=\pi \cdot 10^{2}\cdot h$

$\large h=\frac{40}{\pi \cdot 100}$

Como $\large h \cong 0,127cm$ ou $\large h=1,27mm$ .

Devido ao fato do valor de $\large \pi$ se aproximado, podemos dizer que a altura é próxima de 1,3 mm. O instrumento utilizado em questão é o pluviômetro.

Gabarito: A

Questão 76

O gráfico representa a velocidade escalar de um nadador em função do tempo, durante um ciclo completo de braçadas em uma prova disputada no estilo nado de peito, em uma piscina.

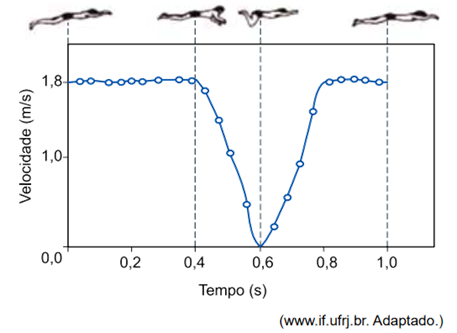
Considerando que, em um trecho de comprimento 36 m, o nadador repetiu esse ciclo de braçadas e manteve o ritmo de seu nado constante, o número de braçadas completas dadas por ele foi em torno de

(A) 20.

(B) 35.

(D) 30.

(E) 25.

Resolução Comentada

$\large A=A_{1}+A_{2}+A_{3}+A_{4}$

$\large A=1,8\cdot (0,4-0,2)+\frac{1,8\cdot (0,6-0,4)}{2}+\frac{1,8\cdot (0,8-0,6)}{2}+$

$\large 1,8\cdot (10-0,8)$

$\large A=1,44$

Então, em um ciclo de braçadas, ele percorre 1,44 m. Como ele se move em um trecho com 3m metros, o número de braçadas do nadador é de:

$\large n=\frac{36}{1,44}=25\ bracadas$

Gabarito: E

Questão 77

Para completar minha obra, restava uma última tarefa: encontrar a lei que relaciona a distância do planeta ao Sol ao tempo que ele leva para completar sua órbita.

Por fim, já quase sem esperanças, tente $\large T^{2}/D^{3}$ . E funcionou! Essa razão é igual para todos os planetas! No início, pensei que se tratava de um sonho. Essa é a lei que tanto procurei, a lei que liga cosmo e mente, que demonstra que toda a Criação provém de Deus. Minha busca está encerrada.

(Apud Marcelo Gleiser. A harmonia do mundo, 2006. Adaptado.)

A lei mencionada no texto refere-se ao trabalho de um importante pensador, que viveu

(A) na Idade Média, período influenciado pelo pensamento da Igreja católica, e que buscava explicar os fenômenos da natureza por meio da intervenção divina.

(B) na Europa posteriormente a Isaac Newton e que, sob forte influência deste filósofo e cientista, estabeleceu as bases da mecânica celeste.

(C) em uma época de exacerbados conflitos religiosos, que culminariam na Contrarreforma católica, opondo-se ao modelo heliocêntrico de Nicolau Copérnico.

(D) no período do Renascimento científico e que formulou três leis fundamentais do movimento planetário, baseando-se em observações do planeta Marte.

(E) no fim da era medieval e início da Idade Moderna, período de triunfo da fé sobre a razão, o que facilitou seus trabalhos na tentativa de compreender a natureza.

Resolução Comentada

(A) Incorreta. O pensador em questão é Kepler, que viveu no período do renascimento científico, posterior à Idade Média.
(B) Incorreta. Kepler viveu anteriormente à Newton.
(C) Incorreta. Kepler ratificou e desenvolveu o modelo de Copérnico.
(D) Correta. Tycho Brahe (1546 – 1601) foi um dos últimos astrônomos a realizar observações sem o uso de telescópios. Os dados por ele compilados serviram de base para Johannes Kepler (1571 – 1630) deduzir as três leis do movimento dos astros. Posteriormente, Isaac Newton (1642 – 1727) foi capaz de demonstrar que as três leis de Kepler são uma consequência de sua lei da gravitação.
(E) Incorreta. No período da Idade Moderna temos a fé ainda forte, porém com prevalência da razão, do método científico.

Gabarito: D

Questão 78

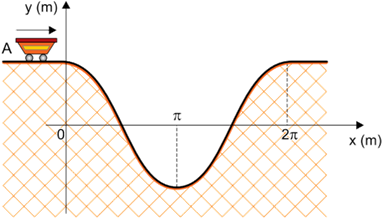
A figura representa o perfil, em um plano vertical, de um trecho de uma montanha-russa em que a posição de um carrinho de dimensões desprezíveis é definida pelas coordenadas x e y, tal que, no intervalo $\large 0\leq x\leq 2\pi ,y=cos(x)$ .

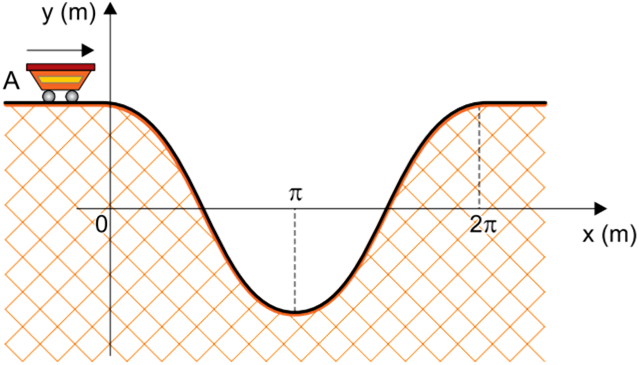
Nessa montanha-russa, um carrinho trafega pelo segmento horizontal A com velocidade constante de $\large 4m/s$ . Considerando $\large g=10m/s^{2}, \sqrt{2}=1,4$ e desprezando o atrito e a resistência do ar, a velocidade desse carrinho quando ele passar pela posição de coordenada $\large x=\frac{5\pi }{4}m$ será:

(A) 10 m/s.

(B) 9 m/s.

(D) 8 m/s.

(E) 7 m/s.

Resolução Comentada

Como não existem forças dissipativas no problema (foram desprezados os atritos), então podemos conservar a energia mecânica durante todo o movimento. Assim, basta calcular a energia mecânica em A e no ponto desejado $\large x=\frac{5\pi }{4}$ e $\large y=cos\frac{5\pi }{4}$ . Então:

$\large E_{mec}^{inicial}=E_{mec}^{final}$

$\large m\cdot g\cdot h_{0}+\frac{m\cdot v^{2}}{2}=m\cdot g\cdot y+\frac{m\cdot v'^{2}}{2}$

Como a massa m está em todos os termos da minha equação, então podemos cortar ela. Além disso, temos que:

$\large h_{0}=1m$ : perceba que em A o corpo está no nível onde cos⁡〖0°〗. Da matemática, sabemos que cos 0° = 1.

$\large v=4m/s$

$y=cos\frac{5\pi }{4}=cos\left ( \pi +\frac{\pi }{4} \right )=-cos\frac{\pi }{4}=-\frac{\sqrt{2}}{2}=-\frac{1,4}{2}=-0,7$

Substituindo os valores na equação, temos:

$\large 10\cdot 1+\frac{4^{2}}{2}=10\cdot (-0,7)+\frac{v'^{2}}{2}$

$\large \frac{v'^{2}}{2}=10+8+7$

$\large v'=\sqrt{25\cdot2}$

$\large v'=\sqrt{5^{2}\cdot2}$

$\large v'=5\cdot \underbrace{\sqrt{2}}_{1,4}$

$\large v'=7m/s$

Gabarito: E

Questão 79

Para obter energia térmica, com a finalidade de fundir determinada massa de gelo, produziu-se a combustão de um mol de gás butano $\large C_{4}H_{10}$ , a 1 atm e a 25 ℃. A reação de combustão desse gás é:

$\large C_{4}H_{10}(g)+\frac{13}{2}\ O_{2}(g)\rightarrow 4CO_{2}(g)+5H_{2}O(l)$

As entalpias-padrão de formação (ΔH) das substâncias citadas estão indicadas na tabela:

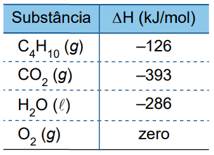
Considerando que a energia térmica proveniente dessa reação foi integralmente absorvida por um grande bloco de gelo a 0 ℃ e adotando 320 J/g para o calor latente de fusão do gelo, a massa de água líquida obtida a 0 ℃, nesse processo, pelo derretimento do gelo foi de, aproximadamente,

(A) 7 kg.

(B) 5 kg.

(D) 10 kg.

(E) 9 kg.

Resolução Comentada

Segundo o enunciado, temos a seguinte reação química:

$\large C_{4}H_{10_{(g)}}+O_{2_{(g)}}\rightarrow 4CO_{2_{(g)}}+5H_{2}O_{l}$

Logo, o calor absorvido pelo gelo devido à reação de combustão é igual a:

$\large \Delta H=\left ( 4\cdot\Delta H_{CO_{2_{(g)}}}+5\cdot \Delta_{H_{2}O_{(l)}}^{0}^{} \right )-1\cdot \left ( \Delta H_{C_{4}H_{10_{(g)}}}^{0} \right )$

$\large \Delta H=\left [ 4\cdot(-393)+5(-286) \right ]-(-126)$

$\large \Delta H=-1572-1430+126$

$\large \Delta H=-2876kJ$

Note que o sinal negativo diz apenas que o calor foi liberado na reação de combustão. Este calor é utilizado para derreter o gelo. Portanto:

$\large 2876\cdot 10^{3}=m\cdot L_{f}$

$\large 2876\cdot 10^{3}J=m\cdot 320\frac{J}{g}$

$\large m=\frac{2876}{320}\cdot 10^{3}g$

$\large m\cong 9\cdot 10^{3}g$ ou $\large m\cong 9kg$

Gabarito: E

Questão 80

Em uma atividade de sensoriamento remoto, para fotografar determinada região da superfície terrestre, foi utilizada uma câmera fotográfica constituída de uma única lente esférica convergente. Essa câmera foi fixada em um balão que se posicionou, em repouso, verticalmente sobre a região a ser fotografada, a uma altura h da superfície.

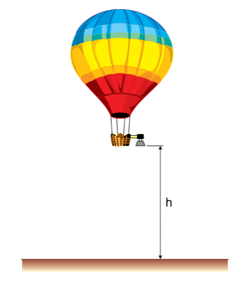
Considerando que, nessa atividade, as dimensões das imagens nas fotografias deveriam ser 5000 vezes menores do que as dimensões reais na superfície da Terra e sabendo que as imagens dos objetos fotografados se formaram a 20 cm da lente da câmera, a altura h em que o balão se posicionou foi de

(A) 1000 m.

(B) 5000 m.

(D) 3000 m.

(E) 4000 m.

Resolução Comentada

De acordo com enunciado, o aumento linear da minha lente convergente é igual a:

$\large A=\frac{1}{5000}$

Cuidado, pois ele disse que o a imagem é 5000 vezes menor que o objeto. Da teoria de lentes, sabemos que:

$\large \left | A \right |=\frac{i}{o}=\frac{1}{5000}=\frac{p'}{p}$

Repare que podemos apenas trabalhar com o módulo do aumento linear, pois estamos apenas interessados na altura h, que corresponde a posição do objeto (p). Como a imagem é formada a 20 cm da lente, temos:

$\large \frac{1}{5000}=\frac{20\cdot 10^{2}}{p}$

$\large p=1000m$

Gabarito: A

Questão 81

A sensibilidade visual de humanos e animais encontra-se dentro de uma estreita faixa do espectro da radiação eletromagnética, com comprimentos de onda entre e . É notável que os vegetais também reajam à radiação dentro desse mesmo intervalo, incluindo a fotossíntese e o crescimento fototrópico. A razão para a importância dessa estreita faixa de radiação eletromagnética é o fato de a energia carregada por um fóton ser inversamente proporcional ao comprimento de onda. Assim, os comprimentos de onda mais longos não carregam energia suficiente em cada fóton para produzir um efeito fotoquímico apreciável, e os mais curtos carregam energia em quantidade que danifica os materiais orgânicos.

(Knut Schmidt-Nielsen. Fisiologia animal: adaptação e meio ambiente, 2002. Adaptado.)

A tabela apresenta o comprimento de onda de algumas cores do espectro da luz visível:

Sabendo que a energia carregada por um fóton de frequência f é dada por $\large E=h\cdot f$ , em que $\large h=6,6\cdot 10^{-34}J\cdot s$ , que a velocidade da luz é aproximadamente $\large c=3\cdot 10^{8}m/s$ e que $\large 1nm=10^{-9}m$ , a cor da luz fótons carregam uma quantidade de energia correspondente a $\large 3,96\cdot 10^{-19}J$ é:

(A) azul.

(B) verde.

(D) laranja.

(E) vermelha.

Resolução Comentada

De acordo com a equação da energia do fóton, temos:

$\large E=h\cdot f$

Além disso, devemos lembrar da equação fundamental da ondulatória:

$\large v=\lambda \cdot f$

$\large c=\lambda \cdot f$

Então:

$\large f=\frac{c}{\lambda }$

Assim, podemos escrever a equação da energia do fóton proposta por Planck em função do comprimento de onda:

$\large E=\frac{h\cdot c}{\lambda }$

$\large \lambda =\frac{h\cdot c}{E}$

Substituindo valores, podemos encontrar o comprimento de onda para a energia correspondente:

$\large \lambda =\frac{6,6\cdot 10^{-34}\cdot 3\cdot 10^{8}}{3,96\cdot 10^{-19}}$

$\large \lambda =5\cdot 10^{-7}=500\cdot \underbrace{10^{-9m}}_{1nm}$

$\large \lambda =500nm$

De acordo com a tabela fornecida, o comprimento de onda de 500 nm está dentro do espectro da cor verde.

Gabarito: B

Questão 82

Na maioria dos peixes elétricos as descargas são produzidas por órgãos elétricos constituídos por células, chamadas eletroplacas, empilhadas em colunas. Suponha que cada eletroplaca se comporte como um gerador ideal.

Suponha que o sistema elétrico de um poraquê, peixe elétrico de água doce, seja constituído de uma coluna com 5000 eletroplacas associadas em série, produzindo uma força eletromotriz total de 600 V.

Considere que uma raia-torpedo, que vive na água do mar, possua um sistema elétrico formado por uma associação em paralelo de várias colunas, cada uma com 750 eletroplacas iguais às do poraquê, ligadas em série, constituindo mais da metade da massa corporal desse peixe.

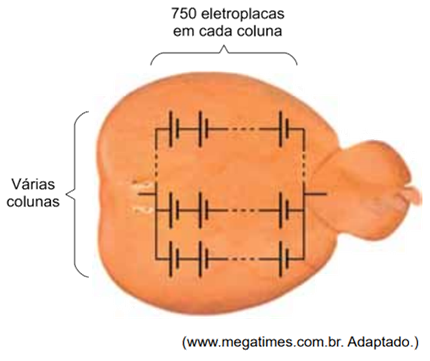
Desconsiderando perdas internas, se em uma descarga a raia-torpedo conseguir produzir uma corrente elétrica total de 50 A durante um curto intervalo de tempo, a potência elétrica gerada por ela, nesse intervalo de tempo, será de

(A) 3500 W.

(B) 3000 W.

(D) 4500 W.

(E) 4000 W.

Resolução Comentada

No poraquê, as 5000 células são ligadas em série, formando a força eletromotriz de 600 V. Nesse tipo de ligação, a diferença de potencial total é dada pela soma da diferença de potencial de cada uma das placas, daí:

$\large \varepsilon _{placa}=\frac{600}{5000}=\frac{6\cancel {00}}{50\cancel {00}}=\frac{6}{50}V$

Já na raia-torpedo, temos 750 placas em série. Isso nos permite calcular a sua diferença de potencial:

$\large \varepsilon _{raia}=750\cdot \frac{6}{50}=\frac{75\cdot 6}{5}$

Podemos encontrar a potência dissipada usando a relação:

$\large Pot=\varepsilon _{raia}\cdot i$

$\large Pot=\frac{75\cdot 6}{5}\cdot 50=\frac{75\cdot 6\cdot 50}{5}=\frac{75\cdot 6\cdot \cancel {50}}{\cancel 5}$

$\large Pot =75\cdot 6\cdot 10=4500W$

Gabarito: D

Questão 85

A Companhia de Engenharia de Tráfego (CET) divulgou um estudo apresentando a mobilidade no sistema viário da cidade de São Paulo. Um dos resultados desse estudo consiste na comparação da velocidade média do tráfego geral, em um importante conjunto de vias, no sentido bairro-centro (BC) e no sentido centro-bairro (CB), nos horários de pico dos períodos da manhã e da tarde, de 2013 a 2017. O gráfico apresenta esse comparativo:

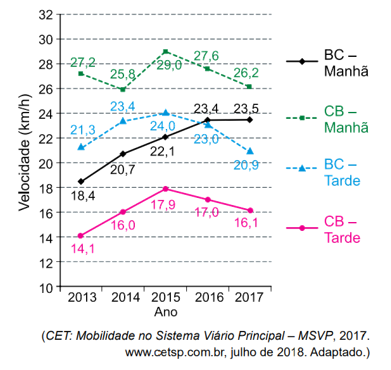
De acordo com o gráfico, em apenas um dos sentidos e em um determinado período foram registradas seguidas reduções anuais no tempo médio de deslocamento ao longo das vias. Comparando 2017 com 2013, a redução do tempo de deslocamento nessas vias, em porcentagem, é de, aproximadamente,

(A) 12,9%.

(B) 5,1%.

(D) 1,8%.

(E) 27,7%.

Resolução Comentada

A velocidade e o tempo são grandezas inversamente proporcionais, para uma mesma distância percorrida:

$\large v=\frac{\Delta S}{\Delta t}\Rightarrow \Delta t=\frac{\Delta S}{v}$

O único trecho em que a velocidade sempre foi crescente é o BC – manhã. Dessa forma, devemos fazer a razão entre os tempos desse trecho para os anos de 2017 e 2013:

$\large \frac{\Delta t_{2017}}{\Delta t_{2013}}=\frac{\frac{\Delta S}{v_{2017}}}{\frac{\Delta S}{v_{2013}}}=\frac{\frac{\cancel {\Delta S}}{v_{2017}}}{\frac{\cancel {\Delta S}}{v_{2013}}}=\frac{\frac{1}{v_{2017}}}{\frac{1}{v_{2013}}}$

$\large \frac{\Delta t_{2017}}{\Delta t_{2013}}=\frac{v_{2013}}{v_{2017}}=\frac{18,4}{23,5}\cong 0,783$

Para determinarmos a diminuição percentual, devemos subtrair o valor encontrado de 1 e efetuar a multiplicação por 100:

Redução = $\large (1 - 0,783)\cdot 100=21,7\%$

Gabarito: C

Conte comigo em sua caminhada, e para ficar sabendo de todas as notícias relativas aos mais diversos vestibulares ocorrendo em nosso país, convido você a seguir as mídias sociais do Estratégia Vestibulares. Sinta-se também convidado a seguir o meu perfil pessoal, no qual trarei questões resolvidas e mais dicas para sua preparação.

Gabarito UNESP 2020 – Física – Prova Resolvida

Prova UNESP 2020

Questão 50

Resolução Comentada

Questão 76

Resolução Comentada

Questão 77

Resolução Comentada

Questão 78

Resolução Comentada

Questão 79

Resolução Comentada

Questão 80

Resolução Comentada

Questão 81

Resolução Comentada

Questão 82

Resolução Comentada

Questão 85

Resolução Comentada

Raquel Oshio

Gabarito UNESP 2020 – Biologia – Prova Resolvida

Prova de Matemática UNESP 2020 com Resolução Comentada

Física no Enem: o que mais cai

Escalas termométricas: Celsius, Kelvin, Fahrenheit e conversões

Como resolver as questões de Física da 2ª Fase da Fuvest 2020

Gabarito UNESP 2020 – Física – Prova Resolvida

Prova UNESP 2020

Questão 50

Resolução Comentada

Questão 76

Resolução Comentada

Questão 77

Resolução Comentada

Questão 78

Resolução Comentada

Questão 79

Resolução Comentada

Questão 80

Resolução Comentada

Questão 81

Resolução Comentada

Questão 82

Resolução Comentada

Questão 85

Resolução Comentada

Raquel Oshio

Gabarito UNESP 2020 – Biologia – Prova Resolvida

Prova de Matemática UNESP 2020 com Resolução Comentada

Você pode gostar também