Olá, pessoal… Tudo bem? Sou o prof. Marçal Ferreira, professor de Matemática do Estratégia Vestibulares. Escrevo este artigo para resolver as questões da prova da 2ª Fase do vestibular da FUVET 2020. Nesta página, você vai conferir a resolução completa e ainda vai poder baixar gratuitamente os comentários em PDF.
Navegue pelo conteúdo
Questão 01
A figura apresenta uma parte de uma tabela na qual cada linha e cada coluna seguem de acordo com o padrão representado.
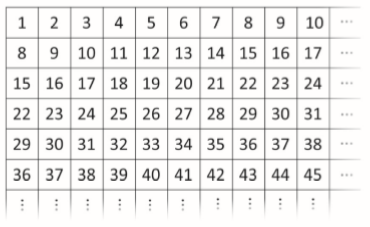
Com relação a essa tabela de números:
a) Escolha um quadrado 3 x 3 e, exibindo a soma de seus 9 números, verifique que o resultado é múltiplo de 9.
b) Um quadrado com 16 números tem por soma de todos esses números o valor de 1.056 (mil e cinquenta e seis). Descubra o menor número desse quadrado.
c) A soma de todos os números de um quadrado n x n, com menor número igual a 4, é de 108.000 (cento e oito mil). Qual é o valor de n?
Gabarito
a) Iniciando a contagem em qualquer posição, temos um quadrado de 3×3 genérico da forma:
Dessa forma, a soma sempre será um múltiplo de nove.
b) De maneira similar ao anterior, temos:
c) O quadrado em questão é do tipo:
Questão 02
O Floco de Neve de Koch (ou Estrela de Koch) é uma construção geométrica recursiva cujos primeiros passos se desenvolvem da seguinte forma:
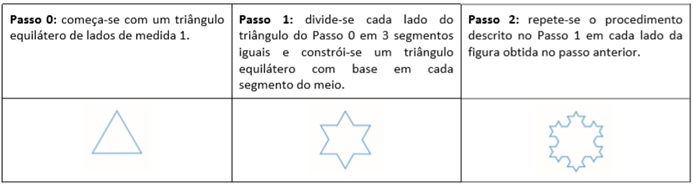
Os passos seguintes (Passo 3, Passo 4, Passo 5, …) seguem o mesmo procedimento descrito no Passo 1, em cada lado da figura obtida no passo anterior. Considerando os passos descritos e os próximos passos, responda:
a) Qual é o número de lados da figura no Passo 3?
b) Qual é o perímetro da figura no Passo 5?
c) A partir de qual Passo o número de lados da figura supera 6.000.000.000.000 (seis trilhões)?
Gabarito
a)
b)
c)
2\cdot{10}^{12}” alt=”\large \left(4\right)^p>2\cdot{10}^{12}” align=”absmiddle”>
{10}^{12}” alt=”\large 2^{2p-1}>{10}^{12}” align=”absmiddle”>
12\cdot\log{10}” alt=”\large \left(2p-1\right)\cdot\log{2}>12\cdot\log{10}” align=”absmiddle”>
\frac{12}{0,301}+1″ alt=”\large 2p>\frac{12}{0,301}+1″ align=”absmiddle”>
\frac{6}{0,301}+\frac{1}{2}” alt=”\large p>\frac{6}{0,301}+\frac{1}{2}” align=”absmiddle”>
21″ alt=”\large p>21″ align=”absmiddle”>
A partir do 21° passo.
Questão 03
Um jogo educativo possui 16 peças nos formatos: círculo, triângulo, quadrado e estrela, e cada formato é apresentado em 4 cores: amarelo, branco, laranja e verde. Dois jogadores distribuem entre si quantidades iguais dessas peças, de forma aleatória.
O conjunto de 8 peças que cada jogador recebe é chamado de coleção.
a) Quantas são as possíveis coleções que um jogador pode receber?
b) Qual é a probabilidade de que os dois jogadores recebam a mesma quantidade de peças amarelas?
c) A regra do jogo estabelece pontuações para as peças, da seguinte forma: círculo = 1 ponto, triângulo = 2 pontos, quadrado = 3 pontos e estrela = 4 pontos. Quantas são as possíveis coleções que valem 26 pontos ou mais?
Gabarito
a)
b)
c)
As coleções possíveis são:
Questão 04
São dados:
• uma circunferência S de centro 0 e raio 5;
• quatro pontos X, Y, Z e W em 5 de tal forma que as retas tangentes a S nesses pontos formam um trapézio ABCD, como na figura;
• .
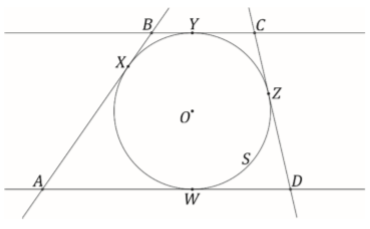
a) a medida de ;
b) a medida de e
;
c) a área da região delimitada pelo trapézio ABCD.
Gabarito
a)
b)
Não há tangente negativa.
c)
Questão 05
É dada a função definida por
para todo
.
a) Apresente três valores para os quais
.
b) Determine os valores de para os quais
.
c) Determine os valores de para os quais
.
Gabarito
a) Apresente três valores para os quais
.
b) Determine os valores de para os quais
.
c) Determine os valores de para os quais
.
Questão 06
Resolva os três itens abaixo:
a) Considere o conjunto formado pelos números complexos z que cumprem a condição . Cada elemento desse conjunto será objeto da transformação que leva um número complexo em seu conjugado. Represente no plano complexo (ou plano de Argand-Gauss) da folha de respostas o conjunto resultante após essa transformação.
b) Determine o lugar geométrico dos pontos z do plano complexo tais que e para os quais
é um número imaginário puro.
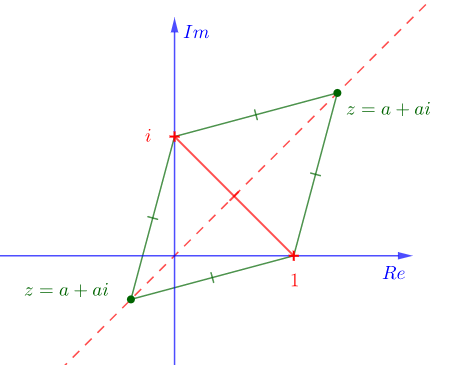
c) Determine as partes reais de todos os números complexos z tais que as representações de z, i e 1 no plano complexo sejam vértices de um triângulo equilátero.
Gabarito
a)
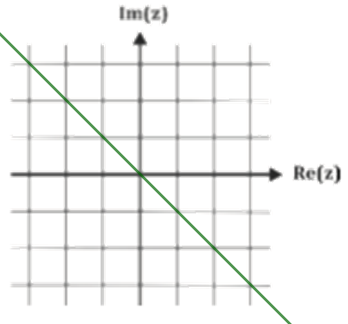
b)
Lugar Geométrico é uma circunferência com centro na origem, exceto o ponto z=-1.
c)
É isso, pessoal! Espero que tenham curtido a resolução da prova de Matemática da prova do Vestibular FUVEST 2020, 2ª Fase. Sigam-me nas redes sociais. Têm muitas dicas lá. Mande uma mensagem, caso tenha tido alguma dúvida.
Você também pode baixar essa resolução em PDF. Basta clicar no link a seguir. Abraços!
Abraços!
Instagram: @professor.marcal