Home Matérias Matemática Resolução da prova de Matemática da 2ª Fase da Unicamp 2020

Resolução da prova de Matemática da 2ª Fase da Unicamp 2020

PorRaquel Oshio
Atualizado em 25 de abril de 2022 ás 17:43 • Publicado em 14 de janeiro de 2020
3 minutos de leitura

Olá, pessoal… Tudo bem? Sou o prof. Marçal Ferreira, professor de Matemática do Estratégia Vestibulares. Escrevo este artigo para resolver as questões da prova da 2ª Fase do vestibular da Unicamp 2020.

Navegue pelo conteúdo

Questão 05

Dois tipos de exames para a detecção de certo vírus foram aplicados em um grupo de 80 pacientes, dos quais, com certeza, 60 são portadores desse vírus e 20 não são. Os resultados dos exames estão organizados nas tabelas abaixo.

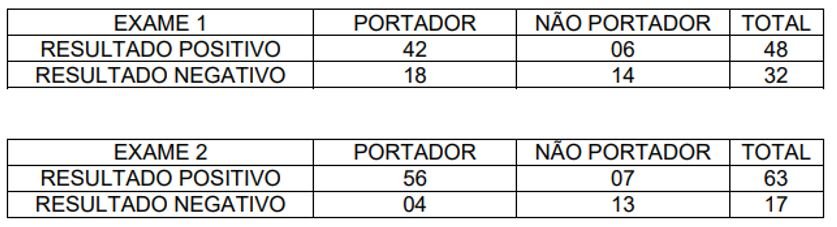
Note que em cada exame ocorrem tanto falsos positivos (pacientes não portadores do vírus com resultado positivo no exame) quanto falsos negativos (pacientes portadores do vírus com resultado negativo no exame).

a) Calcule a porcentagem de pacientes portadores do vírus no grupo em estudo. b) Considerando os resultados positivos em cada exame, qual dos dois exames tem a menor porcentagem de falsos positivos? Justifique sua resposta.

Gabarito

a) Como são 60 portadores do vírus em um grupo de 80 pacientes, temos:

$\dpi{100} \large \frac{60}{80}=\frac{6}{8}=\frac{3}{4}=75\%$

b) O número de falsos positivos para o exame 1 é:

$\dpi{100} \large \frac{6}{48}=\frac{1}{8}=12,5\%$

O número de falsos positivos para o exame 2 é:

$\dpi{100} \large \frac{7}{63}=\frac{1}{9}=11,\bar{1}\%$

Dessa forma, o exame 2 apresenta a menor porcentagem de falsos positivos.

Questão 06

A figura abaixo exibe um triângulo isósceles com dois lados de comprimento $\dpi{100} \large a=5cm$ e um dos ângulos internos igual a $\dpi{100} \large \theta$ , em que $\dpi{100} \large cos\ \theta=3/5$ .

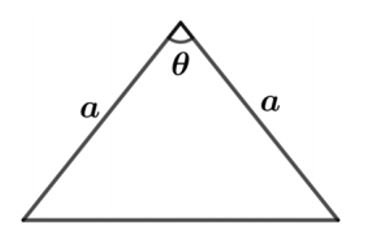
a) Calcule a área desse triângulo.

b) Determine o comprimento do raio da circunferência circunscrita a esse triângulo.

Resolução

$\dpi{100} \large {\rm sen}^2{\left(x\right)}+\cos^2{\left(x\right)}=1$

$\dpi{100} \large {\rm sen}^2{\left(x\right)}+\left(\frac{3}{5}\right)^2=1$

$\dpi{100} \large {\rm sen}^2{\left(x\right)}+\frac{9}{25}=1$

$\dpi{100} \large {\rm sen}^2{\left(x\right)}=\frac{16}{25}$

$\dpi{100} \large sen\left(x\right)=\frac{4}{5}$

a) Calcule a área desse triângulo.

$\dpi{100} \large A=\frac{1}{2}\cdot a\cdot b\cdot sen\left(\theta\right)$

$\dpi{100} \large A=\frac{1}{2}\cdot5\cdot5\cdot\frac{4}{5}$

$\dpi{100} \large A=10\ cm^2$

b) Determine o comprimento do raio da circunferência circunscrita a esse triângulo.

$\dpi{100} \large x^2=a^2+a^2-2\cdot a\cdot b\cdot\cos{\left(\theta\right)}$

$\dpi{100} \large x^2=5^2+5^2-2\cdot5\cdot5\cdot\frac{3}{5}$

$\dpi{100} \large x^2=50-30$

$\dpi{100} \large x=\sqrt{20}$

$\dpi{100} \large x=2\sqrt5\ cm$

$\dpi{100} \large \frac{x}{sen\left(\theta\right)}=2\cdot R$

$\dpi{100} \large \frac{2\sqrt5}{\frac{4}{5}}=2\cdot R$

$\dpi{100} \large \frac{5\sqrt5}{4}\ cm=R$

Questão 07

Seja a matriz de ordem $\dpi{100} \large 2\times3$ , dada por $\dpi{100} \large A=\left[\begin{matrix}1&1&1\\1&2&3\\\end{matrix}\right]$ .

a) Seja C a matriz de ordem $\dpi{100} \large 3\times2$ , cujos elementos são dados por $\dpi{100} \large c_{ij}=\left(-1\right)^{i+j}$ , para $\dpi{100} \large i=1,2,3$ e $\dpi{100} \large j=1,2$ . Determine o produto AC.

b) Determine a solução do sistema linear $\dpi{100} \large A\left[\begin{matrix}x\\y\\z\\\end{matrix}\right]=\left[\begin{matrix}6\\6\\\end{matrix}\right]$ , nas variáveis reais x,y, e z, em que $\dpi{100} \large \left(x,y,z\right)$ é uma progressão aritmética.

Resolução

$\dpi{100} \large c_{11}=\left(-1\right)^{1+1}=1$

$\dpi{100} \large c_{12}=\left(-1\right)^{1+2}=-1$

$\dpi{100} \large c_{21}=\left(-1\right)^{2+1}=-1$

$\dpi{100} \large c_{22}=\left(-1\right)^{2+2}=1$

$\dpi{100} \large c_{31}=\left(-1\right)^{3+1}=1$

$\dpi{100} \large c_{32}=\left(-1\right)^{3+2}=-1$

$\dpi{100} \large C=\left[\begin{matrix}1&-1\\-1&1\\1&-1\\\end{matrix}\right]$

$\dpi{100} \large A\cdot C=\left[\begin{matrix}1&1&1\\1&2&3\\\end{matrix}\right]\cdot\left[\begin{matrix}1&-1\\-1&1\\1&-1\\\end{matrix}\right]$

$\dpi{100} \large A\cdot C=\left[\begin{matrix}1-1+1&-1+1-1\\1-2+3&-1+2-3\\\end{matrix}\right]$

$\dpi{100} \large A\cdot C=\left[\begin{matrix}1&-1\\2&-2\\\end{matrix}\right]$

$\dpi{100} \large A\left[\begin{matrix}x\\y\\z\\\end{matrix}\right]=\left[\begin{matrix}6\\6\\\end{matrix}\right]$

$\dpi{100} \large \left[\begin{matrix}1&1&1\\1&2&3\\\end{matrix}\right]\left[\begin{matrix}x\\y\\z\\\end{matrix}\right]=\left[\begin{matrix}6\\6\\\end{matrix}\right]$

$\dpi{100} \large \left\{\begin{matrix}x+y+z=6\\\ \\x+2y+3z=6\\\end{matrix}\right.$

Como $\dpi{100} \large \left(x,y,z\right)$ é uma progressão aritmética, temos:

$\dpi{100} \large \frac{x+z}{2}=y$

$\dpi{100} \large x+z=2y$

$\dpi{100} \large x-2y+z=0$

Assim, nosso sistema passa a ser:

$\dpi{100} \large \left\{\begin{matrix}x+y+z=6\\\ \\x+2y+3z=6\\\ \\x-2y+z=0\\\end{matrix}\right.$

Escrevendo na forma matricial estendida:

$\dpi{100} \large \left[\begin{matrix}1&1&1&6\\1&2&3&6\\1&-2&1&0\\\end{matrix}\right]\begin{matrix}\cdot\left(-1\right)&\cdot\left(-1\right)\\+&\ \\\ &+\\\end{matrix}$

$\dpi{100} \large \left[\begin{matrix}1&1&1&6\\0&1&2&0\\0&-3&0&-6\\\end{matrix}\right]$

$\dpi{100} \large \left\{\begin{matrix}x+y+z=6\\\ \\x+2y+3z=6\\\ \\x-2y+z=0\\\end{matrix}\right.\rightarrow\left\{\begin{matrix}x+y+z=6\\\ \\y+2z=0\\\ \\-3y=-6\\\end{matrix}\right.\rightarrow$

$\dpi{100} \large \rightarrow\left\{\begin{matrix}x+y+z=6\\\ \\y+2z=0\\\ \\y=2\\\end{matrix}\right.\rightarrow\left\{\begin{matrix}x+y+z=6\\\ \\z=-1\\\ \\y=2\\\end{matrix}\right.\rightarrow\left\{\begin{matrix}x=5\\\ \\z=-1\\\ \\y=2\\\end{matrix}\right.$

Assim, a solução para o sistema solicitado é

$\dpi{100} \large \left[\begin{matrix}x\\y\\z\\\end{matrix}\right]=\left[\begin{matrix}5\\2\\-1\\\end{matrix}\right]$

Questão 08

A figura abaixo exibe, no plano cartesiano, o gráfico de $\dpi{100} \large y=\sqrt x$ para $\dpi{100} \large x\geq0$ , em que os pontos A e B têm abscissas $x_A=a>0″ alt=”\dpi{100} \large x_A=a>0″ align=”absmiddle”> e <img decoding=$

a) Prove que os pontos A, B e $\dpi{100} \large C=\left(-\sqrt{ab},0\right)$ são colineares.

b) Para b=3, determine o valor de a para o qual a distância da origem ao ponto A é igual à distância do ponto A ao ponto B.

Resolução

a) Os pontos em questão são

$\dpi{100} \large A=\left(a,\sqrt a\right)$

$\dpi{100} \large B=\left(b,\sqrt b\right)$

$\dpi{100} \large C=\left(-\sqrt{ab},0\right)$

Para serem colineares, a seguinte equação deve ser verdadeira:

$\dpi{100} \large \left|\begin{matrix}a&\sqrt a&1\\b&\sqrt b&1\\-\sqrt{ab}&0&1\\\end{matrix}\right|=0$

$\dpi{100} \large a\sqrt b+\sqrt a\cdot\left(-\sqrt{ab}\right)-\left(-\sqrt{ab}\right)\cdot\sqrt b-b\sqrt a=0$

$\dpi{100} \large a\sqrt b-a\sqrt b+b\sqrt a-b\sqrt a=0$

$\dpi{100} \large 0=0$

Assim, os três pontos, A, B e C estão alinhados.

b )Para b=3, temos os pontos:

$\dpi{100} \large O=\left(0,0\right)$

$\dpi{100} \large A=\left(a,\sqrt a\right)$

$\dpi{100} \large B=\left(3,\sqrt3\right)$

Pelo enunciado, devemos ter:

$\dpi{100} \large d_{OA}=d_{AB}$

$\dpi{100} \large \sqrt{\left(a-0\right)^2+\left(\sqrt a-0\right)^2}=\sqrt{\left(3-a\right)^2+\left(\sqrt3-\sqrt a\right)^2}$

$\dpi{100} \large \left(a-0\right)^2+\left(\sqrt a-0\right)^2=\left(3-a\right)^2+\left(\sqrt3-\sqrt a\right)^2$

$\dpi{100} \large a^2+a=9-6a+a^2+3-2\cdot\sqrt3\cdot\sqrt a+a$

$\dpi{100} \large 0=12-6a-2\cdot\sqrt3\cdot\sqrt a$

$\dpi{100} \large 0=-6a-2\cdot\sqrt3\cdot\sqrt a+12$

$\dpi{100} \large \sqrt a=x$

$\dpi{100} \large 0=-6x^2-2\cdot\sqrt3\cdot x+12$

$\dpi{100} \large \Delta =\left(-2\cdot\sqrt3\right)^2-4\cdot\left(-6\right)\cdot12=12+288=300$

$\dpi{100} \large x=\frac{-\left(-2\cdot\sqrt3\right)\pm\sqrt{300}}{2\cdot\left(-6\right)}\left\{\begin{matrix}x^\prime=\frac{2\sqrt3+10\sqrt3}{-12}=\frac{12\sqrt3}{-12}=-\sqrt3\\\ \\x^{\prime\prime}=\frac{2\sqrt3-10\sqrt3}{-12}=\frac{-8\sqrt3}{-12}=\frac{2\sqrt3}{3}\\\end{matrix}\right.$

$\dpi{100} \large \sqrt a=x$

$\dpi{100} \large \sqrt a=\frac{2\sqrt3}{3}$

$\dpi{100} \large a=\left(\frac{2\sqrt3}{3}\right)^2$

$\dpi{100} \large a=\frac{4\cdot3}{9}$

$\dpi{100} \large a=\frac{4}{3}$

Questão 09

Seja a função $\dpi{100} \large f\left(x\right)=\frac{2+senx}{2+cosx}$ , definida para todo número real x.

a) Mostre que $\dpi{100} \large f\left(\frac{\pi}{2}\right)+f\left(-\frac{\pi}{2}\right)=f\left(\pi\right)\cdot f\left(\frac{\pi}{4}\right)$ .

b) Seja $\dpi{100} \large \theta$ um número real tal que $\dpi{100} \large f\left(\theta\right)=2$ . Determine os possíveis valores para $\dpi{100} \large sen\ \theta$ .

Resolução

a) $\dpi{100} \large f\left(\frac{\pi}{2}\right)+f\left(-\frac{\pi}{2}\right)=f\left(\pi\right)\cdot f\left(\frac{\pi}{4}\right)$

$\dpi{100} \large \frac{2+sen\left(\frac{\pi}{2}\right)}{2+cos\left(\frac{\pi}{2}\right)}+\frac{2+sen\left(-\frac{\pi}{2}\right)}{2+cos\left(-\frac{\pi}{2}\right)}=\frac{2+sen\left(\pi\right)}{2+cos\left(\pi\right)}\cdot\frac{2+sen\left(\frac{\pi}{4}\right)}{2+cos\left(\frac{\pi}{4}\right)}$

$\dpi{100} \large \frac{2+1}{2+0}+\frac{2+\left(-1\right)}{2+0}=\frac{2+0}{2+\left(-1\right)}\cdot\frac{2+\frac{\sqrt2}{2}}{2+\frac{\sqrt2}{2}}$

$\dpi{100} \large \frac{3}{2}+\frac{1}{2}=\frac{2}{1}\cdot1$

$\dpi{100} \large \frac{4}{2}=2$

$\dpi{100} \large 2=2$

Assim, pode-se afirmar que

$\dpi{100} \large f\left(\frac{\pi}{2}\right)+f\left(-\frac{\pi}{2}\right)=f\left(\pi\right)\cdot f\left(\frac{\pi}{4}\right)$

b) $\dpi{100} \large f\left(\theta\right)=\frac{2+sen\theta}{2+cos\theta}=2$

$\dpi{100} \large 2+sen\theta=4+2\cdot cos\theta$

$\dpi{100} \large sen\theta-2=2\cdot cos\theta$

$\dpi{100} \large sen^2\theta-4sen\theta+4=4\cdot\cos^2{\theta}$

$\dpi{100} \large sen^2\theta-4sen\theta+4=4\cdot\left(1-sen^2\theta\right)$

$\dpi{100} \large sen^2\theta-4sen\theta+4=4-4\cdot sen^2\theta$

$\dpi{100} \large 5\cdot sen^2\theta-4sen\theta=0$

$\dpi{100} \large sen\theta\cdot\left(5\cdot s e n\theta-4\right)=0$

$\dpi{100} \large sen\theta=0\ \ \ \ \ ou\ \ \ \ \ \ 5\cdot sen\theta-4=0$

$\dpi{100} \large sen\theta=0\ \ \ \ \ ou\ \ \ \ \ \ sen\theta=\frac{4}{5}$

Questão 10

A figura abaixo exibe a planificação de um poliedro convexo, com faces triangulares congruentes e faces retangulares, em que são indicados os comprimentos a, b e c.

a) Determine o número de vértices e de arestas desse poliedro.

b) Para a = 13 cm, b = 1 cm e c = 10 cm, calcule o volume desse poliedro.

Resolução

O poliedro tem o seguinte formato:

Assim, temos 16 arestas e 9 vértices.

b) Calculando a altura H da pirâmide de base quadrada da parte superior do poliedro.

$\dpi{100} \large a^2=H^2+\left(\frac{c}{2}\right)^2$

$\dpi{100} \large {13}^2=H^2+\left(\frac{10}{2}\right)^2$

$\dpi{100} \large 169-25=H^2$

$\dpi{100} \large 144=H^2$

$\dpi{100} \large 12=H$

Assim, o volume V do poliedro é dado por:

$\dpi{100} \large V=c^2\cdot b+\frac{1}{3}\cdot c^2\cdot H$

$\dpi{100} \large V={10}^2\cdot16+\frac{1}{3}\cdot{10}^2\cdot12$

$\dpi{100} \large V=1600+400$

$\dpi{100} \large V=2000\ cm^3$

É isso, pessoal! Espero que tenham curtido a resolução da prova de Matemática da prova do Vestibular UNICAMP 2020, 2ª Fase. Sigam-me nas redes sociais. Têm muitas dicas lá. Mande uma mensagem, caso tenha tido alguma dúvida.

Você também pode baixar essa resolução em PDF. Basta clicar no link a seguir. Abraços!

">Prova de Matemática da Unicamp – 2ª fase" class="wp-block-file__button" download>Baixar

Abraços!

Instagram: @professor.marcal

Veja também:

Raquel Oshio

Amante de histórias e caçadora de belezas escondidas. Jornalista de profissão e coração. Desenhista e escritora de ficção nas horas vagas. Acredito no potencial transformador de todo trabalho feito com dedicação.

Resolução da prova de Matemática da 2ª Fase da Unicamp 2020

Questão 05

Inscreva-se em nossa newsletter🦉

Gabarito

Questão 06

Resolução

Questão 07

Resolução

Questão 08

Resolução

Questão 09

Resolução

Questão 10

Resolução

Veja também:

Raquel Oshio

Comentários sobre a prova de História da 2ª Fase da Unicamp

Correção da prova de Português da 2ª Fase da Unicamp 2020

Triângulo de Pascal: o que é, função, propriedades e aplicações

Progressão aritmética: o que é, fórmulas, usos e exemplos

Círculo e circunferência: conceitos e exercícios

Resolução da prova de Matemática da 2ª Fase da Unicamp 2020

Questão 05

Inscreva-se em nossa newsletter🦉

Gabarito

Questão 06

Resolução

Questão 07

Resolução

Questão 08

Resolução

Questão 09

Resolução

Questão 10

Resolução

Veja também:

Raquel Oshio

Comentários sobre a prova de História da 2ª Fase da Unicamp

Correção da prova de Português da 2ª Fase da Unicamp 2020

Você pode gostar também