A Lei de Gauss da Eletricidade: conceito e como cai no ITA

Antes de mostrar o que é a Lei de Gauss da Eletricidade, vamos definir alguns conceitos que serão utilizados na formulação dessa lei.

Navegue pelo conteúdo

Fluxo de um Campo Vetorial

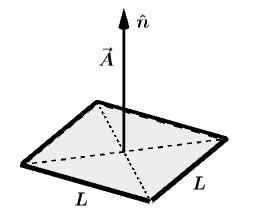
Chamamos de vetor área $\dpi{120} \large (\vec{A})$ o vetor cuja direção é perpendicular e seu módulo é igual a área da superfície que ele representa.

Exemplo: quadrado de lado L, temos que:

\dpi{120} \large \fbox{$\vec{A}=A\cdot\hat{n}=L^2\cdot\hat{n}}

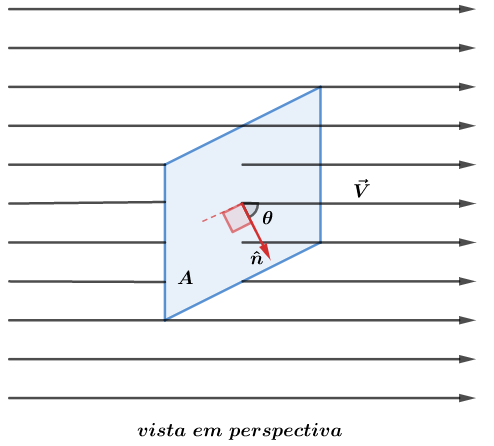
O fluxo de um campo vetorial através de uma superfície imaginária de área A é uma medida do número de linhas do campo que perfuram essa superfície. Matematicamente, dizemos que:

\dpi{120} \large \varphi=\vec{V}\cdot\vec{A}=V\cdot A\cdot cos\theta

Na vista frontal, temos as seguintes situações particulares:

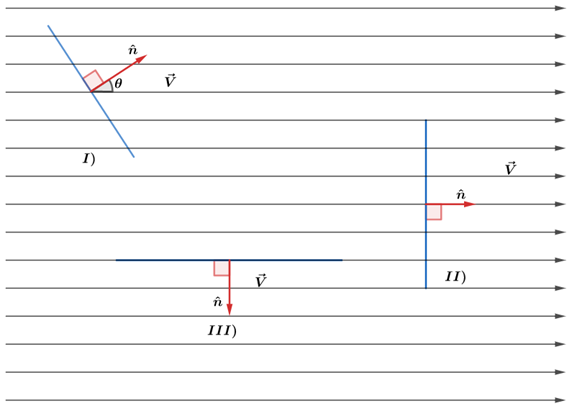
Vista frontal do fluxo de um campo vetorial perfurando uma área imaginária A em diferentes casos.

Para essas três situações temos os seguintes fluxos:

$\dpi{120} \large \varphi_V=V\cdot A\cdot cos\theta$
$\dpi{120} \large \theta =0\degree\Rightarrow \varphi _{v_{max}}=V\cdot A$
$\dpi{120} \large \theta=90\degree\Rightarrow \varphi =0$

Observe que quando $\dpi{120} \large \theta =0\degree$ o fluxo é máximo pois temos o maior número de linhas de força que atravessam a superfície. Por outro lado, quando $\dpi{120} \large \theta =0\degree$ nenhuma linha de força atravessa a superfície.

Mas o que acontece quando as linhas de um campo atravessam uma superfície externa de uma figura tridimensional?

Para responder a essa pergunta vamos considerar uma superfície imaginária, fechada, num campo vetorial qualquer. Para fins de ilustração, vamos considerar que nossa superfície fechada seja a área superficial de uma esfera.

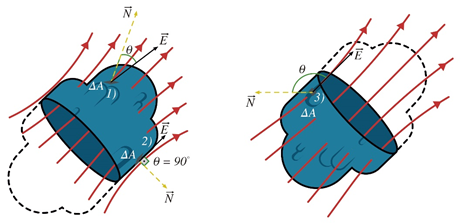
Fluxo de um campo vetorial em uma superfície fechada.

Quando pegamos um elemento de área $\dpi{120} \large \Delta A$ tão pequeno de tal forma que podemos considerar o campo vetorial que atravessa ele, temos que:

Para o elemento $\dpi{120} \large a: \varphi=V\cdot\Delta A\cdot cos\theta$ (positivo, já que $\dpi{120} \large cos\theta>0$ ). Observe que $\dpi{120} \large \varphi$ é positivo nos elementos de superfície em que o campo está saindo.
Para o elemento $\dpi{120} \large b: \varphi=0$ (nulo, já que $\dpi{120} \large \cos{\left(\theta\right)}=cos\ 90\degree=0$ ).
Para o elemento $\dpi{120} \large c: \varphi=V\cdot\Delta A\cdot cos\theta$ (negativo, pois $\dpi{120} \large cos\theta>0$ ). Observe que $\dpi{120} \large \varphi$ é negativo nos elementos de superfície em que o campo está entrando.

A determinação do fluxo total na superfície inteira é dada pela soma de todos os fluxos em todos os seus elementos de superfície. Esse processo se torna interessante, quando tomamos superfícies com elevado grau de simetria.

Para o caso de uma superfície fechada, o fluxo total, devido a cargas externas, é nulo.

Isso é justificado pelo fato da quantidade de linhas de força que entram em uma superfície, gerando um fluxo negativo, ser igual à quantidade de linhas de forças que saem dessa superfície, gerando um fluxo positivo.

Exemplo:

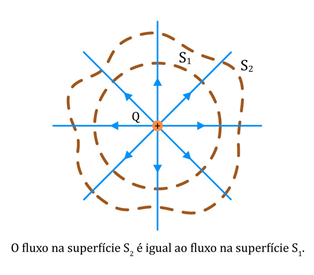
Sejam duas cargas, +q e -q, onde representamos suas linhas de forças. Vamos estudar o fluxo do campo elétrico nas três superfícies fechadas.

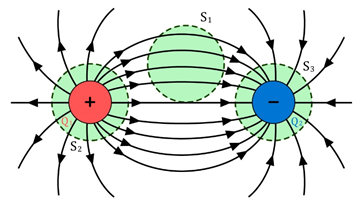
Na superfície $\dpi{120} \large S_{1}$ , as cargas +? e −? são externas, portanto, o fluxo elétrico nessa superfície é nulo. Por outro, na superfície $\dpi{120} \large S_{2}$ as linhas estão saindo, logo, o fluxo é positivo e na superfície $\dpi{120} \large S_{3}$ as linhas estão entrando, logo, o fluxo é negativo.

A Lei de Gauss

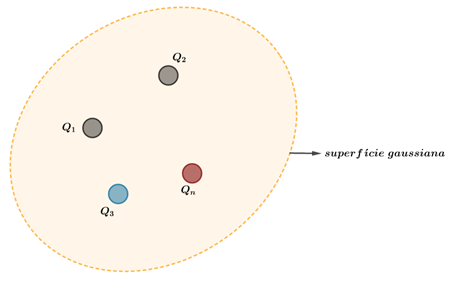
Vamos considerar uma distribuição de cargas elétricas e uma superfície imaginária fechada qualquer, que envolva essas cargas. Chamamos essa superfície imaginária de superfície gaussiana $\dpi{120} \large (\Omega )$ .

A Lei de Gauss determina que o fluxo total $\dpi{120} \large (\varphi _{total})$ que atravessa a gaussiana $\dpi{120} \large (\Omega )$ é igual à carga total interna $\dpi{120} \large \sum Q_{interna}$ dividida pela permissividade do meio $\dpi{120} \large (\varepsilon)$ .

\dpi{120} \large \varphi_{total}=\frac{\sum_{\Omega} Q_{interna}}{\varepsilon}=\frac{Q_1+Q_2+Q_3+\ldots+Q_n}{\varepsilon}

Cargas internas a uma superfície fechada.

A unidade de fluxo elétrico é o $\dpi{120} \large \frac{N\cdot m^2}{C}$ .

Para exemplificar o uso da Lei de Gauss, vamos calcular o fluxo elétrico gerado por uma carga elétrica puntiforme com carga +q, em um meio cuja a permissividade elétrica é $\dpi{120} \large \varepsilon$ .

Vamos pegar uma superfície gaussiana de forma que possamos ter a maior simetria no problema quando calcularmos a soma dos fluxos de cada elemento de área na gaussiana $\dpi{120} \large (\Omega )$ .

Sem muito esforço, vemos que se pegarmos uma esfera com centro na carga puntiforme, iremos simplificar nosso somatório dos pequenos fluxos. Então, podemos calcular o fluxo no elemento de área $\dpi{120} \large \Delta A$ da seguinte forma:

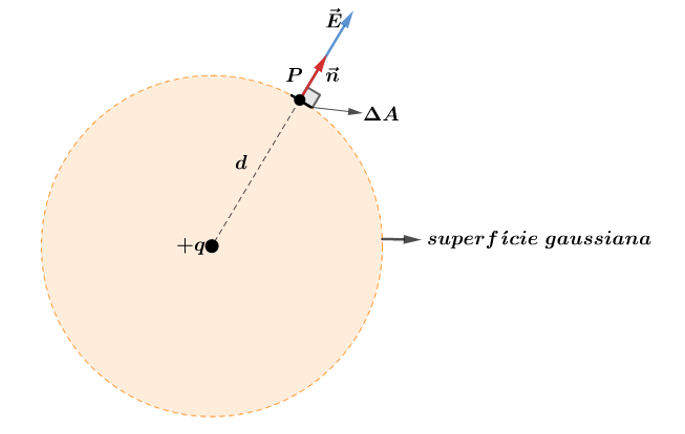
Aplicação da lei de Gauss para carga puntiforme.

\dpi{120} \large \fbox{$\varphi=E\cdot\Delta A\cdot c o s\theta$}

Note que para todos os elementos de área, $\dpi{120} \large \theta =0\degree$ sempre. Por isso, o fluxo no pequeno elemento de área é dado por:

O fluxo total na superfície esférica é dado pela soma dos fluxos em todos os elementos de áreas na gaussiana $\dpi{120} \large (\Omega )$ , lembrando que o módulo do campo elétrico é mesmo dada a distância d:

\dpi{120} \large \varphi_{total}=\sum_{i=0}^{\infty}{E_i\cdot\Delta A_i}=E\cdot\sum_{i=0}^{\infty}{\Delta A_i}

Mas, $\dpi{120} \large \sum_{i=0}^{\infty}{\Delta A_i}$ corresponde a área superficial da esfera (área superficial da gaussiana $\dpi{120} \large (\Omega )$ , então:

\dpi{120} \large \sum_{i=0}^{\infty}{\Delta A_i}=4\pi d^2

Portanto, o fluxo elétrico é dado por:

\dpi{120} \large \varphi_{total}=E\cdot4\pi d^2

Mas, pela Lei de Gauss, o fluxo total é:

\dpi{120} \large \varphi_{total}=\frac{\sum_{\Omega} Q_{interna}}{\varepsilon}=\frac{q}{\varepsilon}

Assim, temos que:

\dpi{120} \large E\cdot4\pi d^2=\frac{q}{\varepsilon}

\dpi{120} \large \therefore E=\frac{1}{4\pi\varepsilon}\cdot\frac{q}{d^2}

Fique atento!

O que entrelaça as teorias já vistas até aqui. Se tivéssemos escolhido outra superfície gaussiana $\dpi{120} \large (\Omega )$ qualquer envolvendo a carga puntiforme, o teorema continuaria válido, pois o fluxo total perfurando esta outra superfície é o mesmo fluxo que perfura a superfície esférica.

Observação: a Lei de Gauss apresentada aqui é válida desde que não haja cargas distribuídas ao longo da superfície gaussiana $\dpi{120} \large (\Omega )$ .

Diante disso, podemos criar um processo para calcular o campo elétrico $\dpi{120} \large \vec{E}$ de distribuições de cargas com certo grau de simetria:

Passo 1: pelo ponto onde deseja-se calcular o módulo do campo, idealize uma gaussiana $\dpi{120} \large (\Omega)$ fechada que contenha em seu interior a distribuição de cargas e que possua a simetria do problema:
$\dpi{120} \large \left|\vec{E}\right|$ seja constante em todos os pontos onde $\dpi{120} \large \vec{E}\cdot\Delta\vec{A}\neq0$ .
$\dpi{120} \large \theta=0\degree$ ou $\dpi{120} \large \theta=90\degree$ ou $\dpi{120} \large \theta=180\degree$ em todos os pontos da gaussiana escolhida.
Passo 2: efetua-se $\dpi{120} \large \varphi_{total}=\sum_{\Omega}{\vec{E}\cdot\Delta\vec{A}}=\frac{\sum Q_{internas}}{\varepsilon}$ ao longo da gaussiana desenhada.

Algumas aplicações da Lei de Gauss

Distribuição de carga elétrica de um condutor eletrizado e em equilíbrio eletrostático

Podemos verificar que o campo elétrico no interior de um condutor eletrizado e em equilíbrio eletrostático é nulo utilizando a Lei de Gauss. Como bem sabemos, dada a condição de equilíbrio eletrostático do condutor, as cargas no condutor se distribuem ao longo da superfície externa.

Com isso, se idealizarmos uma gaussiana $\dpi{120} \large (\Omega)$ no interior do condutor, a carga interna a essa gaussiana é nula. Portanto, pela Lei de Gauss, temos que:

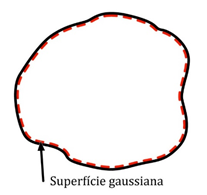
Desenho de uma gaussiana de acordo com o objetivo do problema.

\dpi{120} \large \varphi_{total}=\frac{\sum_{\Omega} Q_{interna}}{\varepsilon}=\frac{0}{\varepsilon}=0=\sum_{\Omega}{\vec{E}\cdot\Delta\vec{A}}

A única forma de garantir que $\dpi{120} \large \sum {_{\Omega }}\vec{E}\cdot\Delta \vec{A}$ é se o campo elétrico for nulo. Dessa forma, confirmamos o resultado que já sabíamos:

\dpi{120} \large {\vec{E}}_{int}=\vec{0}

Campo elétrico criado por uma distribuição plana e ilimitada de cargas

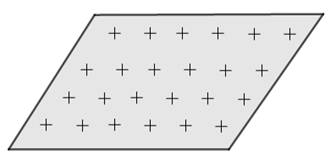
Placa uniformemente carregado com densidade de cargas uniforme σ.

Diante da simetria de uma placa ilimitada (infinita) com distribuição de cargas elétricas uniformes, sabemos que o campo elétrico é nulo num ponto do plano e perpendicular a ele num ponto fora dele.

Realmente, quando tomamos uma carga q situada à esquerda do ponto desejado, existe uma carga q à direita, a mesma distância do ponto, de tal forma que a componente lateral é nula.

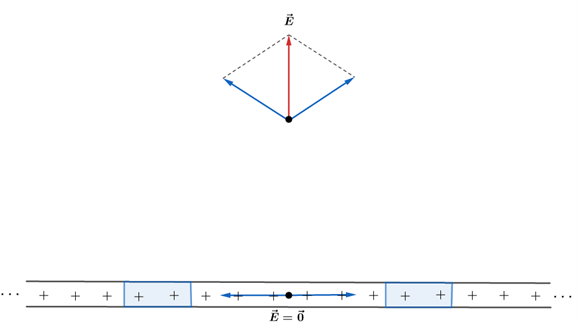
Se passarmos uma gaussiana em um elemento de carga da placa, podemos determinar o campo elétrico num ponto exterior ao plano das cargas. Assim, a gaussiana deve envolver uma área $\dpi{120} \large \Delta A$ e uma carga $\dpi{120} \large \Delta Q$ .

Como o campo na horizontal é nulo, uma excelente gaussiana a ser tomada é superfície externa de um cilindro reto. Tomando a vista frontal, temos que:

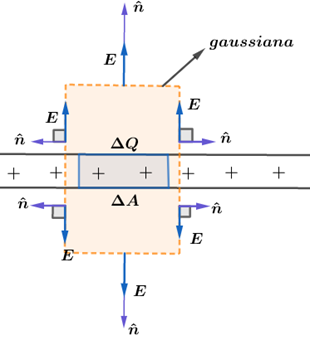
Utilização da Lei de Gauss para o cálculo do campo, devido ao elevado grau de simetria do campo. Note que existem duas possibilidades para o ângulo entre o campo e o vetor área na gaussiana.

Dessa forma, podemos ver que os fluxos na superfície lateral do cilindro são nulos, pois sempre teremos $\dpi{120} \large \vec{E}\bot\hat{n}$ . Já na superfície superior e na superfície inferior, o ângulo entre $\dpi{120} \large \vec{E}$ e $\dpi{120} \large \hat{n}$ é de 0°. Assim, o fluxo é dado por:

$\dpi{120} \large \varphi_{inferior}=E\Delta A$ e $\dpi{120} \large \varphi_{superior}=E\Delta A$

Pela Lei de Gauss, temos que:

\dpi{120} \large \varphi_{total}=\varphi_{inferior}+\varphi_{superior}+\varphi_{lateral}=

\dpi{120} \large \varphi_{total}=E\Delta A+E\Delta A+0=2E\Delta A=

\dpi{120} \large \varphi_{total}=\frac{\sum_{\Omega} Q_{interna}}{\varepsilon}=\frac{\Delta Q}{\varepsilon}

Portanto:

\dpi{120} \large 2E\Delta A=\frac{\Delta Q}{\varepsilon}

Como a densidade superficial uniforme de cargas da placa pode ser escrita como $\dpi{120} \large \sigma=\frac{\Delta Q}{\Delta A}$ , concluímos que:

\dpi{120} \large E=\frac{\sigma}{2\varepsilon}

Conforme vimos anteriormente por intermédio do Cálculo Integral.

Fio retilíneo uniformemente carregado com densidade linear de cargas $\dpi{120} \large \mathbit{\lambda}$

Fio retilíneo uniformemente carregado com densidade de carga

Vamos calcular o campo elétrico gerado por um fio retilíneo tão grande quanto queiramos, com uma densidade linear de cargas $\dpi{120} \large \lambda$ , tal que:

Para isso, vamos pegar um elemento de carga situado em um elemento de comprimento do fio. Semelhante ao caso da placa infinita com distribuição uniforme de cargas, podemos ver sem muito esforço que o campo elétrico gerado pelo fio terá o módulo igual para pontos a uma distância r e direção radial da seguinte forma:

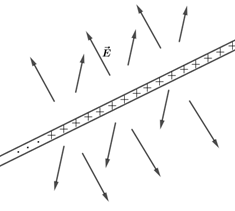
Possíveis direções radiais para o campo gerado pelo fio infinito.

Diante desse conjunto, a melhor superfície gaussiana é novamente a superfície de um cilindro, onde o fio retilíneo coincida com o eixo de rotação do cilindro reto, da seguinte forma:

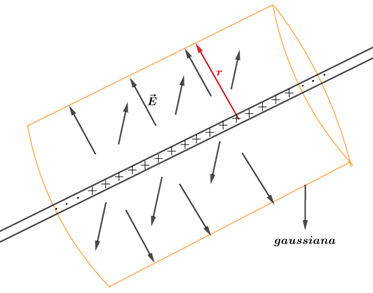
Traçado da gaussiana em um fio retilíneo infinito. A superfície que mais se encaixa para o problema é a superfície externa de um cilindro reto.

Fazendo uma vista frontal da superfície lateral do cilindro, temos que:

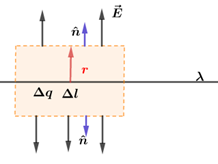
Representação do campo elétrico gerado pelo fio e a superfície gaussiana desenhada.

Assim, nas superfícies que formam as bases do cilindro não haverá fluxo do campo elétrico, apenas na superfície lateral do cilindro. Para o elemento de carga $\dpi{120} \large \Delta q$ de comprimento $\dpi{120} \large \Delta l$ , temos que o fluxo pode ser dado por:

\dpi{120} \large \varphi_{lateral}=E\Delta Acos\theta

\dpi{120} \large \varphi_{lateral}=E\ 2\pi r\ \Delta l\ cos0°

Pela Lei de Gauss, temos que:

\dpi{120} \large \varphi_{total}=\varphi_{lateral}+\varphi_{bases}

\dpi{120} \large \varphi_{total}=E\ 2\pi r\ \Delta l+0=\frac{\sum_{\Omega} Q_{interna}}{\varepsilon}=\frac{\Delta q}{\varepsilon}

\dpi{120} \large E=\frac{1}{2\pi\varepsilon r}\cdot\frac{\Delta q}{\Delta l}

\dpi{120} \large E=\frac{\lambda}{2\pi\varepsilon r}

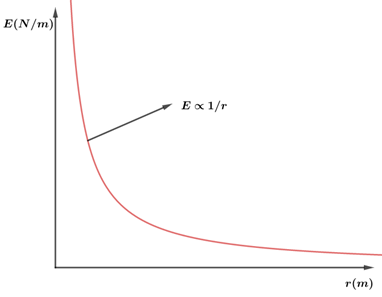
Este resultado mostra que o campo elétrico decresce à medida que vamos tomando pontos cada vez mais distante do fio. Graficamente, temos:

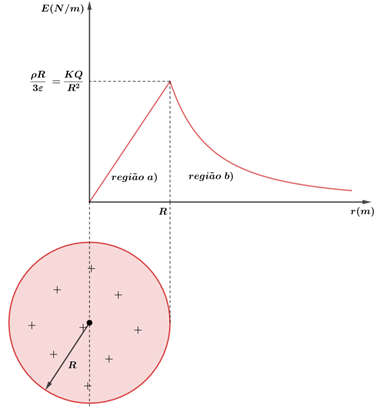
Gráfico do campo elétrico em função da distância para um fio retilíneo e uniformemente carregado.

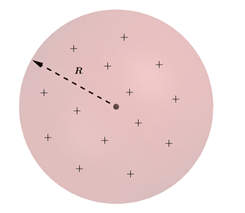
Esfera isolante com densidade volumétrica $\dpi{120} \large \mathbit{\rho}(\mathbit{C}/\mathbit{m}^\mathbf{3})$

Esfera isolante uniformemente carregada.

Onde a densidade volumétrica de cargas pode ser dada por:

\dpi{120} \large \rho=\frac{Q}{\frac{4\pi}{3}\cdot R^3},\ \rho=cte

Para este caso, temos duas regiões onde a ser analisada:

Interior da esfera $\dpi{120} \large (r<r)$ :
Notamos que a gaussiana que atende nossas condições de simetria e campo constante é também a superfície de uma esfera de mesmo centro, mas raio r. Dessa forma, temos a seguinte configuração:

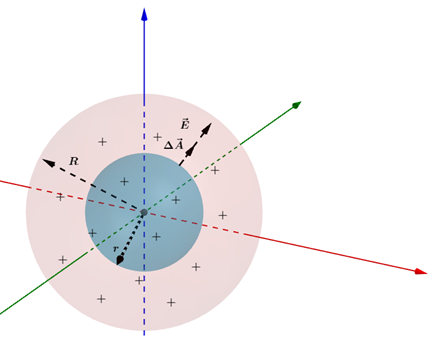
Representação da gaussiana, que é a superfície externa de uma esfera concêntrica a primeira esfera.

Pela Lei de Gauss, temos que:

\dpi{120} \large \varphi_{total}=\sum{_{\Omega}}{\vec{E}\cdot\Delta\vec{A}}=\frac{\sum_{\Omega} Q_{interna}}{\varepsilon}

Diante da simetria na gaussiana de raio r, temos que o campo tem o mesmo módulo e o ângulo entre os vetores $\dpi{120} \large \vec{E}$ e $\dpi{120} \large \Delta\vec{A}$ é 0°,portanto:

\dpi{120} \large E\sum{_{\Omega}}\Delta A=\frac{\sum_{\Omega} Q_{interna}}{\varepsilon}

Onde a carga interna é dada por:

\dpi{120} \large \sum Q_{internas}=\rho\cdot\frac{4\pi}{3}\cdot r^3

Logo, temos que o campo é dado por:

\dpi{120} \large E\cdot4\pi r^2=\frac{\rho\cdot\frac{4\pi}{3}\cdot r^3}{\varepsilon}

\dpi{120} \large E=\frac{\rho}{3\varepsilon}\cdot r

Note que o campo no interior de uma esfera isolante, com densidade volumétrica uniforme de cargas, cresce linearmente à medida que pegamos pontos mais distantes do centro da esfera.

Exterior da esfera
$\dpi{120} \large E\cdot 4\pi r^2=\frac{\rho\cdot\frac{4\pi}{3}\cdot R^3}{\varepsilon}$
$\dpi{120} \large E=\frac{\rho R^3}{3\varepsilon r^2}\ ou\ E=\frac{1}{4\pi\varepsilon}\cdot\frac{Q}{r^2}$
Ou seja, para um ponto fora da esfera, tudo se passa como se a carga fosse pontual e estivesse situada no centro da esfera. Dessa forma, temos o seguinte gráfico do campo elétrico em função da distância para as duas regiões:
Gráfico do campo elétrico em função da distância ao centro.
Indução Total vista pela Lei de Gauss
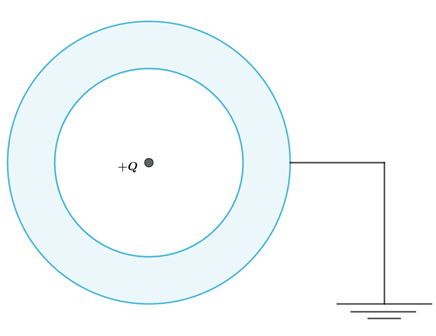
Vamos tomar uma casca esférica condutora, com uma carga puntiforme no centro, conforme mostra a figura:
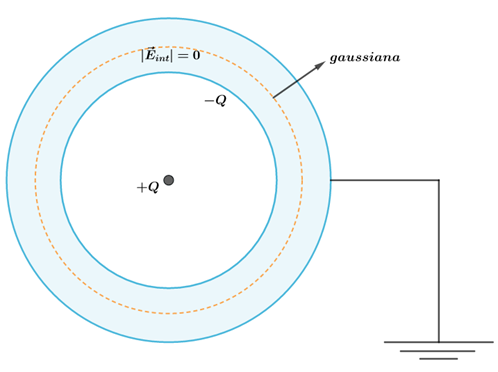
Casca esférica condutora aterrada.
Podemos passar uma gaussiana pelo interior da casca esférica e observar a indução na parte interior da casca, de acordo com a Lei de Gauss:
Campo elétrico no interior da casca condutora é nulo.
De acordo com o equilíbrio eletrostático no interior do condutor, sabemos que o campo elétrico nessa região é nulo. Logo, pela Lei de Gauss, se $\dpi{120} \large \left|{\vec{E}}_{in}\right|=0$ então $\dpi{120} \large \varphi_{total}=0$ , o que implica $\dpi{120} \large Q_{int}=0$ .
Logo, a carga induzida deve ser simétrica em relação a carga no interior da casca (+Q). Portanto:
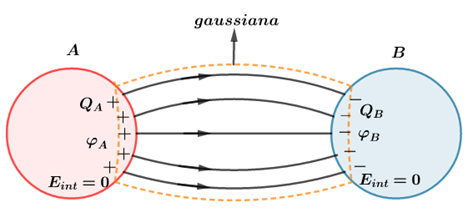
$\dpi{120} \large \fbox{$Q_{induzida}=-(Q_{indutora})$}$
Elementos correspondentes
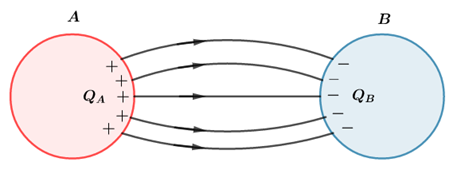
Considere uma esfera A carregada com carga positiva $\dpi{120} \large Q_A$ e uma esfera B carregada com carga negativa $\dpi{120} \large Q_B$ . A região das linhas de força que saem de A para B são denominados elementos correspondentes.
Linhas de força indo de A para B.
De acordo com a Lei de Gauss, podemos demonstrar que se os condutores estiverem em equilíbrio eletrostático, os módulos de $\dpi{120} \large Q_A$ e $\dpi{120} \large Q_B$ serão iguais.
Para tal fim, vamos passar uma gaussiana conforme na figura abaixo:
Gaussiana para um dipolo elétrico.
Note que os fluxos $\dpi{120} \large \varphi_A$ e $\dpi{120} \large \varphi_B$ devem ser nulos já que no interior do condutor em equilíbrio eletrostático o campo elétrico é nulo. Além disso, na região lateral da gaussiana o fluxo do campo é nulo, pois nenhuma linha de força atravessa essa superfície.
Utilizando a Lei de Gauss, temos que:
$\dpi{120} \large \varphi_{total}=\varphi_A+\varphi_B+\varphi_{lateral}=0$
$\dpi{120} \large \frac{\sum_{\Omega} Q_{interna}}{\varepsilon}=0$
$\dpi{120} \large \frac{Q_A+Q_B}{\varepsilon}=0$
$\dpi{120} \large \fbox{$Q_A=-Q_B$}$
$\dpi{120} \large \fbox{$\left|Q_A\right|=\left|Q_B\right|$}$
Podemos concluir que quando todas as linhas de força que partem de uma região e chegam a outra, as cargas dessas regiões sempre possuem o mesmo valor absoluto.
É isso, pessoal! Espero que tenham gostado desta aula sobre a lei de gauss da eletricidade. Se ficou alguma dúvida, mande uma mensagem pelo Fórum de Dúvidas ou através das minhas redes sociais.
Abraços!
Prof. Toni Burgatto
Instagram: @proftoniburgatto

Veja também:

A Lei de Gauss da Eletricidade: conceito e como cai no ITA

Fluxo de um Campo Vetorial

A Lei de Gauss

Fique atento!

Algumas aplicações da Lei de Gauss

Distribuição de carga elétrica de um condutor eletrizado e em equilíbrio eletrostático

Campo elétrico criado por uma distribuição plana e ilimitada de cargas

Fio retilíneo uniformemente carregado com densidade linear de cargas $\dpi{120} \large \mathbit{\lambda}$

Esfera isolante com densidade volumétrica $\dpi{120} \large \mathbit{\rho}(\mathbit{C}/\mathbit{m}^\mathbf{3})$

Indução Total vista pela Lei de Gauss

Elementos correspondentes

Veja também:

Raquel Oshio

Função de Segundo Grau: o que é e como resolver questões

Prova de Biologia da 2ª Fase do vestibular de Medicina da UEG

Cálculo vetorial: o que é, como fazer e aplicações

Difusão e efusão dos gases: definição, fórmulas e questões

Queda livre: o que é, fórmulas e questões de vestibulares

A Lei de Gauss da Eletricidade: conceito e como cai no ITA

Fluxo de um Campo Vetorial

A Lei de Gauss

Fique atento!

Algumas aplicações da Lei de Gauss

Distribuição de carga elétrica de um condutor eletrizado e em equilíbrio eletrostático

Campo elétrico criado por uma distribuição plana e ilimitada de cargas

Fio retilíneo uniformemente carregado com densidade linear de cargas <img decoding="async" src="https://latex.codecogs.com/svg.latex?\dpi{120}&amp;space;\large&amp;space;\mathbit{\lambda}" alt="\dpi{120} \large \mathbit{\lambda}" align="absmiddle">

Esfera isolante com densidade volumétrica <img decoding="async" src="https://latex.codecogs.com/svg.latex?\dpi{120}&amp;space;\large&amp;space;\mathbit{\rho}(\mathbit{C}/\mathbit{m}^\mathbf{3})" alt="\dpi{120} \large \mathbit{\rho}(\mathbit{C}/\mathbit{m}^\mathbf{3})" align="absmiddle">

Indução Total vista pela Lei de Gauss

Elementos correspondentes

Veja também:

Raquel Oshio

Função de Segundo Grau: o que é e como resolver questões

Prova de Biologia da 2ª Fase do vestibular de Medicina da UEG

Você pode gostar também

Fio retilíneo uniformemente carregado com densidade linear de cargas $\dpi{120} \large \mathbit{\lambda}$

Esfera isolante com densidade volumétrica $\dpi{120} \large \mathbit{\rho}(\mathbit{C}/\mathbit{m}^\mathbf{3})$