Na física moderna e astronômica, é comum que sejam utilizados números muito grandes, que ultrapassam a casa dos bilhões, por exemplo. Para facilitar a escrita e compreensão desses valores, os estudiosos criaram a notação científica e a ordem de grandeza.
Para te apresentar esses conceitos e te ajudar no estudo pré-prova, o Estratégia Vestibulares desenvolveu um resumo do tema ordem de grandeza, com as informações mais importantes do assunto: regras, prefixos, escalas e usos. Ao final, veja como isso aparece nas questões e como você pode resolvê-las. Confira!
Navegue pelo conteúdo
O que é ordem de grandeza?
Conhecer a definição das expressões é um bom ponto de partida para a compreensão das disciplinas que aparecem no vestibular. Veja, a seguir, o que é ordem de grandeza e qual sua importância:
A ordem de grandeza é um modo de representar um valor por meio de um número arredondado ou simplificado, geralmente com potências na base 10. Ela é muito utilizada quando os cálculos resultam em valores extremos: muito grandes ou muito pequenos.
Por exemplo, imagine que a distância entre dois astros da via láctea seja de 1.150.658 km e que esse valor apareça em um vestibular. Para simplificação, pode-se optar por expressar o resultado em uma potência de 10, de forma que o número esteja arredondado e expresse a magnitude dessa distância. Nesse caso, o valor está expresso na ordem dos milhões de quilômetros.
De maneira análoga,é possível citar o exemplo do diâmetro de uma célula humana. Por ser muito pequeno, esse valor apresenta diversas casas decimais: 0.000002. Na resolução ou alternativas, esse número pode ser representado pelas ordens de grandeza e por potências de 10, o que facilita a escrita e desenvolvimento dos cálculos.
Perceba que o uso dessas ferramentas, além de simplificar os escritos matemáticos, também expressam a significação de um valor numérico. Ou seja, independentemente dos algarismos que aparecem nas unidades e dezenas, sabe-se que a distância entre dois astros é muito grande. Assim como o diâmetro de uma célula é tão pequeno que precisa ser representado com potências de coeficiente negativo.
Notação científica
Para dar continuidade ao estudo das ordens de grandeza, é importante conhecer o conceito de notação científica. Essa ferramenta matemática é utilizada para converter valores numéricos em potências de 10 e deixá-los com a seguinte aparência: x.10y.
Com o objetivo de conseguir tal transformação e alcançar esse padrão, é necessário que 1≤x<10 e y∊Z (pertencente ao conjunto dos números inteiros).
Veja exemplos:
I) 1370000000 = 1,37 . 109
Perceba que, como 1≤x<10, a notação não admitirá 13,7 ou 0,137 e o único valor possível é 1,37.
Para conseguir o 109 é preciso contar o número de casas entre a vírgula e o último zero, como na figura acima.
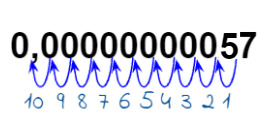
II) 0,00000000057= 5,7 . 10-10
Nesse caso, o valor mais adequado para atender 1≤x<10 é 5,7. Na determinação do expoente, utiliza-se o mesmo método do exemplo anterior, veja:
Regras para Ordem de Grandeza
Além de conhecer a notação científica, aprenda agora quais são e como são aplicadas as regras para ordem de grandeza:
Como essa ferramenta matemática se relaciona com uma aproximação dos valores a partir da potência de dez, utiliza-se as seguintes etapas:
- Utiliza-se a notação científica: x.10y;
- Procura-se entre quais potências de dez o valor está contido;
- Estima-se qual potência está mais próxima desse número, a partir do seguinte parâmetro: quando x>5,5 a ordem de grandeza é a potência de maior expoente, quando x<5,5 a ordem será a menor potência.
Veja aplicações:
I) 1370000000 = 1,37 . 109
O número está entre 109 e 1010, como 1,37<5,5, a ordem de grandeza será a de menor potência. Ou seja, 1370000000 é da ordem de grandeza de 109.
II) 0,00000000057= 5,7 . 10-10
O valor está entre 10-10 e 10-11 e, se considerarmos que 5,7>5,5, deve-se manter a potência de maior expoente. Nesse caso, como os expoentes são negativos, o menor número é aquele que mais se aproxima do 0. Ou seja, 0,00000000057 é da ordem de 10-10.
Prefixos para ordens de grandeza
Para além de potências, a magnitude dos valores pode ser descrita por meio de prefixos padronizados, que facilitam as representações matemáticas e aparecem no Enem com frequência. Confira os principais prefixos para ordens de grandeza na tabela seguinte:
| Prefixo e símbolo | Potência (ordem de grandeza) |
| pico (p) | 10-12 |
| nano (n) | 10-9 |
| micro (µ) | 10-6 |
| mili (m) | 10-3 |
| centi (c) | 10-2 |
| deci (d) | 10-1 |
| deca (da) | 101 |
| hecto (h) | 102 |
| quilo (k) | 103 |
| mega (M) | 106 |
| giga (G) | 109 |
| tera (T) | 1012 |
Escala de comprimento
Por meio dos prefixos e potências, é possível estabelecer uma escala das ordens de grandeza do comprimento, como demonstrado na tabela a seguir:
| Quilômetro | Hectômetro | Decâmetro | Metro | Decímetro | Centímetro | Milímetro |
| km | hm | dam | m | dm | cm | mm |
| 103 m | 102 m | 101 m | 100 m | 10-1 m | 10-2 m | 10-3 m |
Questão sobre Ordem de Grandeza
Para entender como aparecem as questões de ordem de grandeza e notação científica nos vestibulares, veja a resolução proposta por nossa equipe.
CEFET-MG 2008
Nos trabalhos científicos, números muito grandes ou próximos de zero, são escritos em notação científica, que consiste em um número x, tal que 1 < x < 10 multiplicado por uma potência de base 10. Assim sendo, 0,00000045 deve ser escrito da seguinte forma:
a) 0,45 . 10-7
b) 4,5 . 10-7
c) 45 . 10-6
d) 4,5 . 108
A notação científica admite o formato de x.10y com , 1≤x<10 e y∊Z. Para atender a esses critérios, o único x possível é x=4,5. Para adicionar a potência e o valor de y, contam-se as casas decimais, como na figura:
Com isso, a notação correta para esse número será: 4,5.10-7, como na alternativa B.
Assista uma aula grátis de Ordem de Grandeza
Na aula de matemática do Estratégia Vestibulares, com o professor Andrew Cazemiro, você pode acompanhar os principais conceitos, usos e aplicações da notação científica e ordem de grandeza:
Precisa aprender mais sobre as exatas e como elas podem aparecer no Enem? Conheça os cursos do Estratégia voltados para a matemática, a física e a química. Além disso, veja mais sobre o nosso banco de questões, criado para te impulsionar no estudo pré-vestibular, clique no banner abaixo:
Veja também:
- O que mais cai em Física no Enem?
- Diagrama de Fases: o que é e como interpretar
- Fórmulas de Física mais comuns do Enem e outros vestibulares
- Calorimetria no Enem: como cai?
- Hidrostática: pressão, densidade e fórmulas
- Como cai a óptica no Enem
- Eletricidade: conheça as principais fórmulas e conceitos
- Resolução da prova de Física da 2ª Fase da Unicamp 2020
- Resolução Comentada da prova de Física FUVEST 2020




