Prova ITA 2020 – Física – Resolução Comentada

Fala, pessoal… Tudo bem? Sou o prof. Toni Burgatto, do Estratégia Vestibulares e Carreiras Militares. Neste artigo, você vai conferir a resolução das questões da prova de Física do Vestibular ITA 2020. A seguir, você também vai poder baixar a correção da prova que disponibilizei gratuitamente em PDF. Vamos à resolução!!

">Física – Prova ITA 2020 – Resolvida" class="wp-block-file__button" download>Baixar

Prova ITA 2020 – Física

Questão 01

Considere uma teoria na qual a força de interação entre duas “cargas generalizadas” $\large q_1$ e $\large q_2$ em universos N-dimensionais é expressa por $\large F_e=q_1q_2/(kr^{N-1})$ em que k uma constante característica do meio. A teoria também prevê força entre dois “polos generalizados” $\large p_1$ e $\large p_2$ expressa por $\large F_m=p_1p_2/(\mu r^{N-1})$ , na qual $\large \mu$ é outra constante característica do meio. Sabe-se ainda que um polo p pode interagir com uma corrente de carga, t, gerando uma força $\large F=ip/(r^{N-2})$ . Em todos os casos, r representa a distância entre os entes interagentes. Considerando as grandezas fundamentais massa, comprimento, tempo e corrente de carga, assinale a alternativa que corresponde à fórmula dimensional de $\large k\mu$ .

a) $\large L^2T^{-2}$

b) $\large L^{-2}T^2$

c) $\large L^{-2}T^{-2}$

d) $\large L^{1-N}T^2$

e) $\large L^{-2}T^{N-1}$

Resolução Comentada

Pelo enunciado:

$\large F=\frac{q_1\cdot q_2}{k\cdot r^{N-1}}$

$\large F=\frac{p_1\cdot p_2}{\mu\cdot r^{N-1}}$

$\large F=\frac{i\cdot p}{r^{N-2}}$

Fazendo-se a análise dimensional das equações, sabendo que:

$\large \left[F\right]=M\cdot L\cdot T^{-2}$

$\large \left[i\right]=\left[q\right]\cdot T^{-1}$

Tem-se:

$\large M\cdot L\cdot T^{-2}=\left[q\right]^2\cdot\left[k\right]^{-1}\cdot L^{1-N}$

$\large M\cdot L\cdot T^{-2}=\left[p\right]^2\cdot\left[\mu\right]^{-1}\cdot L^{1-N}$

$\large M\cdot L\cdot T^{-2}=\left[q\right]\cdot T^{-1}\cdot\left[p\right]\cdot L^{2-N}\rightarrow$

$\large \left[q\right]\cdot\left[p\right]=M\cdot L^{N-1}\cdot T^{-1}$

Multiplicando as duas primeiras equações:

$\large M^2\cdot L^2\cdot T^{-4}=\left(\left[q\right]\cdot\left[p\right]\right)^2\cdot\left(\left[k\right]\cdot\left[\mu\right]\right)^{-1}\cdot L^{2-2N}$

Substituindo a relação encontrada anteriormente:

$\large M^2\cdot L^2\cdot T^{-4}\cdot\left[k\cdot\mu\right]=M^2\cdot L^{2N-2}\cdot T^{-2}\cdot L^{2-2N}$

$\large \fbox{$\left[\mu\cdot k\right]=L^{-2}\cdot T^2$}$

Gabarito: B

Questão 02

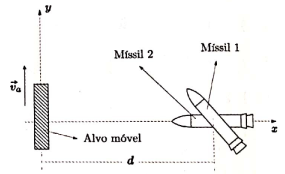
Um sistema de defesa aérea testa separadamente dois mísseis contra alvos móveis que se deslocam com velocidade $\large {\vec{v}}_a$ constante ao longo de uma reta distante de d do ponto de lançamento dos mísseis. Para atingir o alvo, o míssil 1 executa uma trajetória retilínea, enquanto o míssil 2, uma trajetória com velocidade sempre orientada para o alvo. A figura ilustra o instante de disparo de cada míssil, com o alvo passando pela origem do sistema de coordenadas xy. Sendo os módulos das velocidades os mísseis iguais entre si, maiores que $\large v_a$ e mantidos constantes, considere as seguintes afirmações:

I. Os intervalos de tempo entre o disparo e a colisão podem ser iguais para ambos os mísseis.
II. Para que o míssil 1 acerte o alvo é necessário que o módulo da componente y de sua velocidade seja igual a $\large v_a$ .
III. Desde o disparo até a colisão, o míssil 2 executa uma trajetória curva de concavidade positiva com relação ao sistema xy.

Considerando V como verdadeira e F como falsa, as afirmações I, II e III são, respectivamente,

a) V, V e V.

b) F, F e F.

c) V, F e V.

d) F, V e F.

e) F, V e V.

Resolução Comentada

I: Falsa. Mas, se considerarmos que a velocidade do alvo pode ser constante e igual a 0 m/s, a afirmativa é verdadeira. Já que nesse caso ambos os mísseis percorreriam trajetória retilínea, e, então, demorariam o mesmo tempo para chegar ao alvo já que tem velocidades iguais. Assim, implicaria no III como falso.

Entretanto, considerando a velocidade $\large v_a\neq0$ , como as trajetórias têm comprimentos diferentes e os módulos das velocidades são iguais para ambos misseis, então o tempo deve ser diferente.

II: Verdadeira. Se pensarmos que $\large v_a\neq v_{M1y}$ , teríamos que a ordenada do míssel 1 é sempre diferente da ordenada do alvo. Portanto, eles nunca se encontrariam. Dessa forma, é condição necessária que $\large v_a=v_{M1y}$ .

III: Verdadeira. Do desenho, como $\large v_a\geq0$ e a trajetória do míssel 2 tem sempre $\large |v_{2x}|\geq0$ , então, a trajetória do míssel tem concavidade para cima.

Gabarito: E

Questão 03

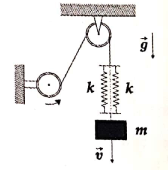
Um bloco de massa m sustentado por um par de molas idênticas, paralelas e de constante elástica k, desce verticalmente com velocidade constante e de módulo v controlada por um motor, conforme ilustra a figura. Se o motor travar repentinamente, ocorrerá uma força de tração máxima no cabo com módulo igual a

a) $\large mg+\sqrt{\left(mg\right)^2+2kmv^2}$

b) $\large mg+\sqrt{\left(mg\right)^2+kmv^2}$

c) $\large mg+\sqrt{2kmv^2}$

d) $\large mg+\sqrt{4kmv^2}$

e) $\large mg+\sqrt{kmv^2}$

Resolução Comentada

Pelo enunciado que afirma que a velocidade é constante, tem-se pelo equilíbrio, na situação inicial:

$\large 2\cdot k\cdot x=m\cdot g$

$\large x=\frac{m\cdot g}{2\cdot k}$

Ao travar-se o motor, inicia-se um problema de conservação de energia mecânica:

$\large E_c+E_{p,el}=E_{p,el}+E_{p,g}$

$\large \frac{m\cdot v^2}{2}+\frac{2\cdot K\cdot x^2}{2}=\frac{2\cdot K\cdot\left(x+y\right)^2}{2}-m\cdot g\cdot y$

Assim:

$\large \frac{m\cdot v^2}{2}+K\cdot x^2=K\cdot\left(x^2+2\cdot x\cdot y+y^2\right)-m\cdot g\cdot y$

$\large m\cdot g\cdot y+\frac{m\cdot v^2}{2}=K\cdot\left(2\cdot x\cdot y+y^2\right)$

Substituindo x:

$\large m\cdot g\cdot y+\frac{\left(m\cdot v^2\right)}{2}=K\cdot\left(\frac{2\cdot m\cdot g}{2\cdot K}\cdot y+y^2\right)$

$\large \frac{m\cdot v^2}{2}=K\cdot y^2$

$\large y=\sqrt{\frac{m\cdot v^2}{2\cdot K}}$

Na situação final:

$\large T=\left(2\cdot K\right)\cdot\left(x+y\right)$

$\large T=2\cdot K\cdot\left(\frac{m\cdot g}{2\cdot K}+\sqrt{\frac{m\cdot v^2}{2\cdot K}}\right)$

$\large \fbox{$T=m\cdot g+\sqrt{2\cdot m\cdot k\cdot v^2}$}$

Gabarito: C

Questão 04

Por uma mangueira de diâmetro $\large D_1$ flui água a uma velocidade de 360 m/min, conectando-se na sua extremidade a 30 outras mangueiras iguais entre si, de diâmetro $\large D_2<d_1$ . Assinale a relação $\large D_2/D_1$ para que os jatos de água na saída das mangueiras tenham alcance horizontal máximo de 40 m.

a) 1/10

b) $\large \sqrt{3/10}$

c) 4/5

d) 1/2

e) $\large \sqrt{2/3}$

Resolução Comentada

A velocidade inicial ao utilizar-se a mangueira de $\large D_1$ é de 360 m/min ou 6 m/s. Assim, o fluxo é dado por:

$\large \phi=6\cdot\pi\cdot\left(\frac{D_1}{2}\right)^2$

O fluxo total que percorre as mangueiras unidas é o mesmo que na situação inicial. Dessa forma:

$\large \phi=30\cdot v_2\cdot\pi\cdot\left(\frac{D_2}{2}\right)^2$

Para o alcance máximo, sabe-se que o ângulo da velocidade com a horizontal deve ser de 45°, dessa forma:

$\large t_{lancamento}=2\cdot\frac{v_2\cdot\frac{\sqrt2}{2}}{g}=\frac{v_2\cdot\sqrt2}{g}$

E, a distância percorrida é:

$\large d=v_2\cdot\frac{\sqrt2}{2}\cdot v_2\cdot\frac{\sqrt2}{g}=\frac{v_2^2}{g}$

Como $\large d=400\ m$ :

$\large v_2^2=400$

$\large v_2=20\frac{m}{s}$

Substituindo na relação do fluxo:

$\large 6\cdot\pi\cdot\left(\frac{D_1}{2}\right)^2=30\cdot20\cdot\pi\cdot\left(\frac{D_2}{2}\right)^2$

$\large \frac{1}{100}\cdot D_1^2=D_2^2$

$\large \frac{D_2}{D_1}=\sqrt{\frac{1}{100}}=\frac{1}{10}$

Gabarito: A

Questão 05

Um satélite artificial viaja em direção a um planeta ao longo de uma trajetória parabólica. A uma distância d desse corpo celeste, propulsores são acionados de modo a, a partir daquele instante, mudar o módulo da velocidade do satélite de $\large v_p$ para $\large v_e$ e também a sua trajetória, que passa a ser elíptica em torno do planeta, com semieixo maior a. Sendo a massa do satélite desproporcionalmente menor que a do planeta, a razão $\large v_e/v_p$ é dada por:

a) $\large \sqrt{\frac{d}{a}-\frac{1}{2}}$

b) $\large \sqrt{\frac{d}{2a}}$

c) $\large \sqrt{1-\frac{d}{2a}}$

d) $\large \sqrt{1+\frac{d}{2a}}$

e) $\large \sqrt{1-\frac{d}{a}}$

Resolução Comentada

Na órbita parabólica, o satélite tem energia mecânica total igual a zero. Portanto, pela equação de conservação de energia mecânica em órbitas parabólicas, temos que:

$\large \frac{-GMm}{d}+\frac{mv^2}{2}=0$

Logo:

$\large v_p=\sqrt{\frac{2GM}{d}}$

Para a órbita elíptica, temos:

$\large \frac{-GMm}{d}+\frac{mv^2}{2}=\frac{-GMm}{2a}$

Assim:

$\large v_e=\sqrt{2GM}\sqrt{\frac{1}{d}-\frac{1}{2a}}$

Portanto, a razão entre as velocidades é dada por:

$\large \frac{v_e}{v_p}=\sqrt{1-\frac{d}{2a}}$

Gabarito: C

Questão 06

Uma pequena esfera com peso de módulo P é arremessada verticalmente para cima com velocidade de módulo $\large V_0$ a partir do solo. Durante todo o percurso, atua sobre a esfera uma força de resistência do ar de módulo F constante. A distância total percorrida pela esfera após muitas reflexões elásticas com o solo é dada aproximadamente por:

a) $\large \frac{V_0^2\left(P-F\right)}{2gF}$

b) $\large \frac{V_0^2\left(P+F\right)}{2gF}$

c) $\large \frac{2V_0^2P}{gF}$

d) $\large \frac{V_0^2P}{2gF}$

e) $\large \frac{V_0^2P}{gF}$

Resolução Comentada

Pelo teorema da energia cinética:

$\large \Delta E_c=\tau_{FNC}$

$\large -\frac{m\cdot v_0^2}{2}=-F\cdot d$

$\large d=\frac{\left(\frac{P}{g}\right)\cdot v_0^2}{2\cdot F}$

$\large d=\frac{P\cdot v_0^2}{2\cdot g\cdot F}$

Gabarito: D

Questão 07

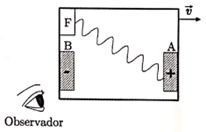
A figura ilustra um experimento numa plataforma que, no referencial de um observador externo, se move com velocidade $\large \vec{v}$ constante de módulo comparável ao da velocidade da luz. No instante to, a fonte F emite um pulso de luz de comprimento de onda $\large \lambda$ que incide sobre a placa metálica A, sendo por ela absorvido e, em consequência, emitindo elétrons, que são desacelerados pela diferença de potencial $\large V_{AB}$ . Considerando que os elétrons atingem a placa ? a partir do instante ?, assinale a alternativa que referencia apenas variações independentes que diminuem o intervalo de tempo $\large \Delta t=t-t_0$ medido pelo observador.

a) aumento de $\large \lambda$ , aumento de $\large V_{AB}$ , diminuição de v.

b) diminuição de $\large \lambda$ , diminuição de $\large V_{AB}$ , diminuição de v.

c) diminuição de $\large \lambda$ , aumento de $\large V_{AB}$ , diminuição de v.

d) diminuição de $\large \lambda$ , diminuição de $\large V_{AB}$ , aumento de v.

e) aumento de $\large \lambda$ , aumento de $\large V_{AB}$ , aumento de v.

Resolução Comentada

O tempo medido pelo observador é dado por:

$\large \Delta t_{observador}=\frac{\Delta t_{plataforma}}{\sqrt{1-\frac{v^2}{c^2}}}$

Como deseja-se diminuir o tempo medido pelo observador tem-se duas possibilidades. Pode-se reduzir o tempo medido no referencial da plataforma ou pode diminuir-se o fator de Lorentz. Dessa forma:

– Para reduzir o tempo medido na plataforma:

1) Pode-se aumentar a velocidade de ejeção do elétron. Para isso é necessário que o elétron seja ejetado com uma energia cinética maior. Sabendo que a energia cinética do elétron ejetado é dada por:

$\large E_c=h\cdot f-\phi$

É necessário aumentar-se a frequência do fóton incidente, e, sabendo que:

$\large f=\frac{c}{\lambda}$

Dessa forma, a diminuição do $\large \lambda$ irá aumentar a velocidade de ejeção do elétron que por sua vez diminui o tempo medido na plataforma e, assim, diminui o tempo medido pelo observador.

2) Pode-se diminuir as forças contrárias ao movimento do elétron. Neste caso, somente a força elétrica por conta do campo elétrico entre as placas é contrária ao movimento.

$\large q\cdot E=m\cdot a$

$\large q\cdot\frac{V_{AB}}{d}=m\cdot a$

Assim, a diminuição da diferença de potencial entre as placas acarreta uma diminuição da frenagem do elétron, permitindo assim, que se atinja a placa em menos tempo.

E, para reduzir o fator de Lorentz:

$\large \gamma=\frac{1}{\sqrt{1-\left(\frac{v}{c}\right)^2}}$

Implica um aumento do denominador. Para isso:

$\large \sqrt{1-\left(\frac{v_1}{c}\right)^2}<\sqrt{1-\left(\frac{v_2}{c}\right)^2}$

$\large 1-\left(\frac{v_1}{c}\right)^2<1-\left(\frac{v_2}{c}\right)^2$

$\large \left(\frac{v_2}{c}\right)^2<\left(\frac{v_1}{c}\right)^2$

$\large v_2<v_1$

Assim, diminuindo-se a velocidade, aumenta-se o denominador, e, por conseguinte, diminui-se o tempo medido pelo operador.

Gabarito: B

Questão 08

Num ambiente controlado, o período de um pêndulo simples é medido a uma temperatura T. Sendo $\large \alpha=2\cdot{10}^{-4}\ °C-1$ o coeficiente de dilatação linear do fio do pêndulo, e considerando a aproximação binomial $\large \left(1\ +\ x\right)^n\approx1+nx$ , para $\large \left|x\right|\ll1$ , pode-se dizer que, com aumento de 10 °?, o período do pêndulo:

a) aumenta de 0,1%.

b) aumenta de 0,05%.

c) diminui de 0,1%.

d) diminui de 0,05%.

e) permanece inalterado.

Resolução Comentada

O período de oscilação de um pêndulo simples é dado por:

$\large T=2\cdot\pi\cdot\sqrt{\frac{l}{g}}$

Portanto, na situação inicial:

$\large T=2\cdot\pi\cdot\sqrt{\frac{l}{g}}$

E, na situação final:

$\large T\prime=2\cdot\pi\cdot\sqrt{\frac{l^\prime}{g}}$

Onde:

$\large l^\prime=l\cdot\left(1+\alpha\cdot\Delta\theta\right)$

$\large l^\prime=l\cdot\left(1+2\cdot{10}^{-4}\cdot10\right)=l\cdot\left(1+2\cdot{10}^{-3}\right)$

$\large T=2\cdot\pi\cdot\sqrt{\frac{l\cdot\left(1+2\cdot{10}^{-3}\right)}{g}}$

$\large T^\prime=2\cdot\pi\sqrt{\frac{l}{g}}\cdot\left(1+2\cdot{10}^{-3}\right)^\frac{1}{2}\cong$

$\large 2\cdot\pi\cdot\sqrt{\frac{l}{g}}\cdot\left(1+1\cdot{10}^{-3}\right)=$

$\large T\cdot\left(1+1\cdot{10}^{-3}\right)$

Dessa forma, o aumento foi de $\large 1\cdot{10}^{-3}$ do período original, ou, de outra forma, 0,1%.

Gabarito: A

Questão 09

Uma certa quantidade de gás com temperatura inicial $\large T_0$ , pressão $\large P_0$ e volume $\large V_0$ , é aquecida por uma corrente elétrica que flui por um fio de platina num intervalo de tempo $\large \Delta t$ . Esse procedimento é feito duas vezes: primeiro, co volume constante $\large V_0$ e pressão variando de $\large P_0$ para $\large P_1$ e, a seguir, com pressão constante $\large P_0$ e com volume variando de $\large V_0$ para $\large V_1$ . Assinale a alternativa que explicita a relação $\large C_P/C_V$ do gás.

a) $\large \frac{\frac{P_0}{P_1}-1}{\frac{V_0}{V_1}-1}$

b) $\large \frac{\frac{P_1}{P_0}-1}{\frac{V_1}{V_0}-1}$

c) $\large \frac{2\frac{P_0}{P_1}-1}{\frac{V_0}{V_1}-1}$

d) $\large \frac{2\frac{P_1}{P_0}-1}{\frac{V_1}{V_0}-1}$

e) $\large \frac{\frac{P_1}{P_0}-1}{\frac{2V_1}{V_0}-1}$

Resolução Comentada

calor cedido pelo fio de platina em ambos os casos é dado por:

$\large Q=R_{fio}\cdot i^2\cdot t$

Assim, o calor recebido pelo gás em ambos os casos foi idêntico, logo:

$\large n\cdot c_v\cdot\Delta T_1=n\cdot c_p\cdot\Delta T_2$

Pela transformação gasosa da isocórica:

$\large \frac{P_0}{T_0}=\frac{P_1}{T_1}\rightarrow T_1=T_0\cdot\frac{P_1}{P_0}$

Pela transformação gasosa da isobárica:

$\large \frac{V_0}{T_0}=\frac{V_1}{T_2}\rightarrow T_2=T_0\cdot\frac{V_1}{V_0}$

Assim:

$\large n\cdot c_v\cdot\left(T_1-T_0\right)=n\cdot c_p\cdot\left(T_2-T_0\right)$

$\large c_v\cdot T_0\cdot\left(\frac{P_1}{P_0}-1\right)=c_p\cdot T_0\cdot\left(\frac{V_1}{V_0}-1\right)$

$\large \frac{c_p}{c_v}=\frac{\frac{P_1}{P_0}-1}{\frac{V_1}{V_0}-1}$

Gabarito: B

Questão 10

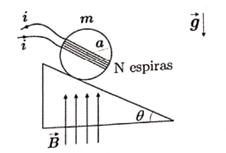
Ao redor de um cilindro de massa m, raio a e comprimento b, são enroladas simétrica e longitudinalmente N espiras. Estas são dispostas paralelamente a um plano inclinado onde se encontra um cilindro, que não desliza devido ao atrito com a superfície do plano. Considerando a existência de um campo magnético uniforme e vertical $\large \vec{B}$ na região, assinale a intensidade da corrente i que deve circular nas espiras para que o conjunto permaneça em repouso na posição indicada pela figura.

a) $\large \frac{mg}{2bB}$

b) $\large \frac{Nmg}{2aB}$

c) $\large \frac{Nmg}{bB}$

d) $\large \frac{mg}{2aBN}$

e) $\large \frac{mg}{2bBN}$

Resolução Comentada

Para o equilíbrio de momentos do cilindro, temos que:

$\large \tau_{F_{mag}}=\tau_{Peso}$

$\large \tau_{peso}=magsen(\theta)$

$\large \tau_{F_{mag}}=2NBiabsen(\theta)$

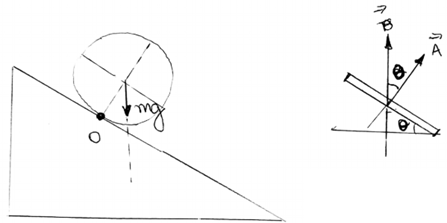
Igualando as duas equações, temos que:

$\large \tau_{peso}=\tau_{F_{mag}}$

$\large m\cdot g\cdot a\cdot sen\left(\theta\right)=2\cdot N\cdot B\cdot i\cdot a\cdot b\cdot sen(\theta)$

$\large i=\frac{m\cdot g}{2\cdot N\cdot B\cdot b}$

Gabarito: E

Questão 11

O som produzido pelo alto-falante F (fonte) ilustrado na figura tem frequência de 10 kHz e chega a um microfone M através de dois caminhos diferentes. As ondas sonoras viajam simultaneamente pelo tubo esquerdo FXM, de comprimento fixo, e pelo tubo direito FYM, cujo comprimento pode ser alterado movendo-se em M. Quando a seção deslizante do caminho FYM é puxada para fora por 0,025 m, a intensidade sonora detectada pelo microfone passa de um máximo para um mínimo. Assinale o módulo da velocidade do som no interior do tubo.

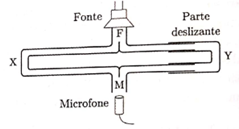
a) $\large 5,0\cdot{10}^2\ m/s$

b) $\large 2,5\cdot{10}^2\ m/s$

c) $\large 1,0\cdot{10}^3\ m/s$

d) $\large 2,0\cdot{10}^3\ m/s$

e) $\large 3,4\cdot{10}^2\ m/s$

Resolução Comentada

O mínimo de intensidade é sentido graças ao deslocamento da secção deslizante FYM. Como, para que ocorra diferença de fase devemos ter:

$\large n_{impar}\frac{\lambda}{2}=2d$

Em que 2d é distância que o som percorre a mais pelo lado FYM com relação ao lado FXM. Assim, substituindo $\large v=\lambda f$ e $\large f={10}^4Hz$ , $\large d=0,025m$ , obtemos que:

$\large n_{impar}\frac{v}{2f}=2d$

$\large n_{impar}\frac{v}{2\cdot{10}^4}=0,05$

Assim:

$\large v=\frac{{10}^3}{n_{impar}}$

De acordo com as alternativas, a única que pode ser satisfeita é a C.

Gabarito: C

Questão 12

Considere o circuito da figura no qual há uma chave elétrica, um reostato linear de comprimento total de 20 cm, uma fonte de tensão $\large V=1,5\ V$ e um capacitor de capacitância $\large C=10\ \mu F$ conectado a um ponto intermediário do reostato, de modo a manter contato elétrico e permitir seu carregamento. A resistência R entre uma das extremidades do reostato e o ponto de contato elétrico, a uma distância as, varia segundo o gráfico ao lado.

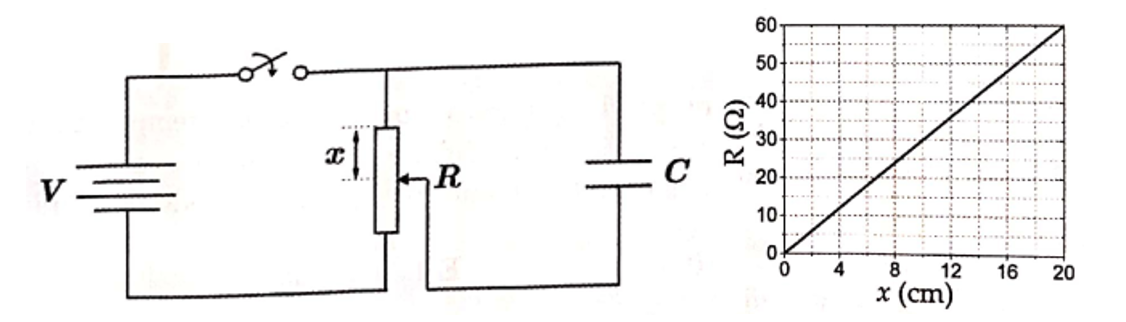
Com a chave fechada e no regime estacionário, a carga no capacitor é igual a

a) $\large 1,5\ mC$

b) $\large 75\ \mu C$

c) $\large 75x\mu C/cm$

d) $\large 15x\mu C/cm$

e) $\large 7,5\ \mu C$

Resolução Comentada

O circuito da figura para uma situação genérica fica:

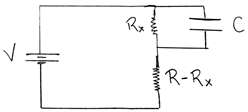
Onde:

$\large V=1,5\ V$

$\large R=60\ \Omega$

$\large R_x=3\cdot x\ (cm)\cdot\Omega$

$\large C=10\ \mu F$

A corrente que percorre o circuito no regime estacionário é de:

$\large i=\frac{V}{R_x+R-R_x}=\frac{V}{R}=\frac{1,5}{60}=\frac{1}{40}$

A diferença de potencial entre as extremidades da resistência $\large R_x$ fica:

$\large V_x=R_x\cdot i=3\cdot x\ (cm)\cdot\frac{1}{40}=\frac{3\cdot x\ (cm)}{40}$

E, a carga do capacitor é dada por:

$\large Q=C\cdot U$

$\large Q=10\ \mu F\cdot\frac{3\cdot x}{40}=\frac{3}{4}\cdot x\ (cm)\ \mu C$

$\large \fbox{$Q=0,75\cdot x\ (cm)\ \mu C$}$

Gabarito: Sem Alternativa

Questão 13

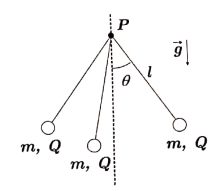
Três esferas idênticas de massa m, carga elétrica Q e dimensões desprezíveis, são presas pelas extremidades de fios isolantes e inextensíveis de comprimento l. As demais pontas dos fios são fixadas a um ponto P, que sustenta as massas. Na condição de equilíbrio do sistema, verifica-se que o ângulo entre um dos fios e a direção vertical é θ, conforme mostra a figura. Sendo $\large \varepsilon_0$ permissividade elétrica do meio, o valor da carga elétrica Q é dada por

a) $\large l\ \sqrt{12\pi\varepsilon_0mg\ sen\theta\ cos\theta}$

b) $\large l\ \sqrt{4\pi\varepsilon_0mg\ tg\theta\ \sqrt3}$

c) $\large l\ sen\theta\sqrt{4\pi\varepsilon_0mg\ tg\theta\ \sqrt3}$

d) $\large l\ sen\theta\sqrt{\ \frac{4\pi\varepsilon_0mg\ tg\theta}{\sqrt3}}$

e) $\large l\ sen\theta\sqrt{4\pi\varepsilon_0mg\ tg\theta\ }$

Resolução Comentada

De acordo com o enunciado, na condição de equilíbrio, temos a seguinte configuração espacial das cargas:

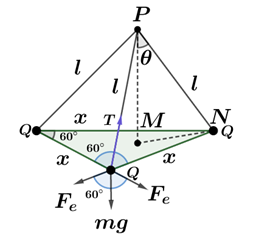
Pelo equilíbrio das forças, temos:

$\large tg(\theta )=\frac{2\cdot F_{e}\cdot cos\ 60\degree}{m\cdot g}$

Pela geometria no triângulo da base formado pelas cargas, temos:

$\large l\cdot sen\left(\theta\right)=MN=x\cdot\frac{\sqrt3}{2}\cdot\frac{2}{3}$

$\large x=l\cdot\sqrt3\cdot sen\left(\theta\right)$

Portanto:

$\large tg\left(\theta\right)=\frac{2\cdot\frac{1}{4\pi\cdot\varepsilon_0}\cdot\frac{Q\cdot Q}{x^2}\cdot\frac{\sqrt3}{2}}{m\cdot g}$

$\large Q=\sqrt{\frac{m\cdot g\cdot4\pi\varepsilon_0\cdot t g\left(\theta\right)}{\sqrt3}}\cdot l\cdot\sqrt3\cdot sen\left(\theta\right)$

$\large \fbox{$q=l\cdot s e n\left(\theta\right)\cdot\sqrt{4\pi\varepsilon_0\cdot m\cdot g\cdot t g\left(\theta\right)\sqrt3}$}$

Gabarito: C

Questão 14

Dois raios luminosos paralelos e simétricos em relação ao eixo óptico, interdistantes de 2mm, devem ser focados em um ponto P no interior de um bloco transparente, a 1 mm de sua superfície, confirme mostra a figura. Para tal, utiliza-se uma lente delgada convergente com distância focal de 1 mm. Considerando que o bloco tem índice de refração $\large n=\ \sqrt2$ , a distância L entre o vértice V da lente e a superfície do bloco deve ser ajustada para:

a) $\large 1mm$

b) $\large \frac{\sqrt{2}}{2}mm$

c) $\large \left ( 1-\frac{\sqrt{2}}{2} \right )mm$

d) $\large \frac{\sqrt{3}}{3}mm$

e) $\large \left ( 1-\frac{\sqrt{3}}{3} \right )mm$

Resolução Comentada

Segundo as condições do problema, temos:

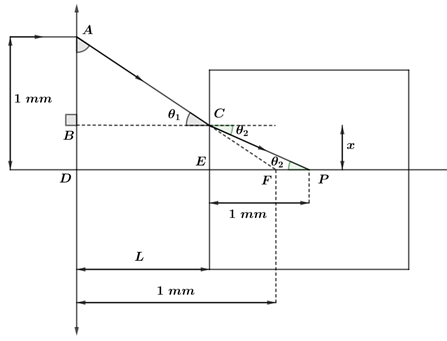
Pela geometria, temos $\large \Delta AFD\sim \Delta ACB$ , então:

$\large AD=DF$

$\large D\widehat{A}F=\frac{\pi }{4}$

Aplicando a Lei de Snell em C, temos:

$\large n_1\cdot sen\left(\theta_1\right)=n_2\cdot sen\left(\theta_2\right)$

$\large 1\cdot sen\left(\frac{\pi}{4}\right)=\sqrt2\cdot sen\left(\theta_2\right)$

$\large sen\left(\theta_2\right)=\frac{1}{2}$

$\large \theta_2=30\degree$

No triângulo $\large \Delta CEP$ , temos:

$\large tg30\degree=\frac{CE}{PE}$

$\large \frac{\sqrt3}{3}=\frac{CE}{1}\Rightarrow CE=\frac{\sqrt3}{3}\ mm$

Portanto:

$\large AB+BD=1\ mm$

$\large AB+CE=1\ mm$

$\large L+\frac{\sqrt3}{3}=1$

$\large L=1-\frac{\sqrt3}{3}\ mm$

Gabarito: E

Questão 15

Considere um sistema de três máquinas térmicas $\large M_1,M_2\ e\ M_3$ acopladas, tal que o rejeito energético de uma é aproveitado pela seguinte. Sabe-se que a cada ciclo, $\large M_1$ recebe 800kJ de calor de uma fonte quente a 300K e rejeita 600kJ, dos quais 150kJ são aproveitados por $\large M_2$ para realização de trabalho. Por fim, $\large M_3$ aproveita o rejeito de $\large M_2$ e descarta 360kJ em uma fonte fria a 6K. São feitas as seguintes afirmações:

I. É inferior a 225K a temperada da fonte fria de $\large M_3$ .

II. O rendimento do sistema é de 55%.

III. O rendimento do sistema corresponde a 80% do rendimento de uma máquina de Carnot operando entre as mesmas temperaturas.

Conclui-se então que

a) somente a afirmação I está incorreta.

b) somente a afirmação II está incorreta.

c) somente a afirmação III está incorreta.

d) todas as afirmações estão corretas.

e) as afirmações I e III estão incorretas.

Resolução Comentada

De acordo com as informações do enunciado, temos:

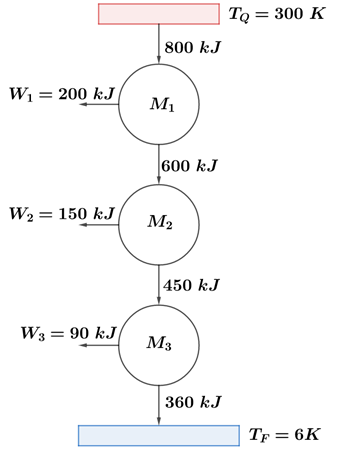
O calor transmitido entre a fonte quente que está a 300 K e a máquina térmica $\large M_1$ se transforma em trabalho e em calor que é rejeitado para a máquina térmica $\large M_2$ . A máquina térmica 2 aproveita o calor rejeitado por $\large M_1$ e o converte em trabalho e calor rejeitado para $\large M_3$ . Por fim, $\large M_3$ utiliza este calor rejeitado por $\large M_2$ e o converte em trabalho e calor rejeitado para a fonte fria que está a 6K.

Assim, pelas equações de conservação de energia, temos:

$\large Q_Q=W_1+Q_{M2}$

$\large Q_{M2}=W_2+Q_{M3}$

$\large Q_{M3}=W_3+Q_f$

Como Sabemos que

$\large Q_Q=800\ kJ,Q_{M2}=600\ kJ,W_2=150\ kJeQ_F=360\ kJ$

chegamos que

$\large W_1=200\ kJ,Q_{M3}=450\ kJ\ e\ W_3=90\ kJ$

Dessa forma, podemos analisar as afirmativas:

I: Verdadeira. O rendimento de $\large M_1$ é:

$\large \eta_1=\frac{W_1}{Q_q}=\frac{200}{800}=\frac{1}{4}$

Portanto $\large T_f\le225K$ . Como Carnot é uma máquina teórica, na prática, a temperatura da fonte fria de 1 deve ser inferior a 225 K.

II: Verdadeira. Para o sistema, temos:

$\large \eta=\frac{\sum W_i}{Q_Q}=\frac{440}{800}=0,55=55\ \%$

III: Falsa. Considerando o rendimento de Carnot para as mesmas temperaturas, temos:

$\large \eta=1-\frac{T_f}{T_q}=1-\frac{6}{300}=\frac{49}{50}$

Agora, fazendo Gabarito: C

É isso, pessoal! Espero que tenham curtido a resolução da prova de Física da prova da 1ª Fase do Vestibular ITA 2020. Sigam-me nas redes sociais. Têm muitas dicas lá. Mande uma mensagem, caso tenha tido alguma dúvida. Abraços!

Instagram: @proftoniburgatto

CURSOS ITA

Prova ITA 2020 – Física – Resolução Comentada

Prova ITA 2020 – Física

Questão 01

Resolução Comentada

Questão 02

Resolução Comentada

Questão 03

Resolução Comentada

Questão 04

Resolução Comentada

Questão 05

Resolução Comentada

Questão 06

Resolução Comentada

Questão 07

Resolução Comentada

Questão 08

Resolução Comentada

Questão 09

Resolução Comentada

Questão 10

Resolução Comentada

Questão 11

Resolução Comentada

Questão 12

Resolução Comentada

Questão 13

Resolução Comentada

Questão 14

Resolução Comentada

Questão 15

Resolução Comentada

Raquel Oshio

Prova ITA 2020 – Matemática – Resolução Comentada

Figuras de Som: o que são, como se classificam e exemplos

Mecânica – Física para UNESP

Eletricidade: conheça as principais fórmulas e conceitos

Magnetismo no Enem: conceitos, assuntos, fórmulas e mais!

Prova ITA 2020 – Física – Resolução Comentada

Prova ITA 2020 – Física

Questão 01

Resolução Comentada

Questão 02

Resolução Comentada

Questão 03

Resolução Comentada

Questão 04

Resolução Comentada

Questão 05

Resolução Comentada

Questão 06

Resolução Comentada

Questão 07

Resolução Comentada

Questão 08

Resolução Comentada

Questão 09

Resolução Comentada

Questão 10

Resolução Comentada

Questão 11

Resolução Comentada

Questão 12

Resolução Comentada

Questão 13

Resolução Comentada

Questão 14

Resolução Comentada

Questão 15

Resolução Comentada

Raquel Oshio

Prova ITA 2020 – Matemática – Resolução Comentada

Figuras de Som: o que são, como se classificam e exemplos

Você pode gostar também