Quando o assunto é vestibular, um importante passo estratégico é o estudo dos temas mais recorrentes nas provas. Por isso, trouxemos hoje, um conteúdo que aparece todos os anos no Enem e nos principais vestibulares: Geometria Plana – Área do Trapézio.
A figura em destaque neste tópico, o trapézio, é definido como polígono geométrico com dois lados paralelos. O trapézio pode ser classificado de três formas:
- Trapézio retângulo: possui ângulos de 90°;
- Trapézio isósceles: os lados não paralelos são congruentes; ou
- Trapézio Escaleno: todos os lados com medidas diferentes
Para compreender melhor, confira as imagens abaixo:

Navegue pelo conteúdo
Qual a fórmula da área do trapézio?
Após conhecer a figura e suas classificações, é muito relevante aprender as fórmulas de área do trapézio, bem como explorar isso no contexto de vestibulares.
Para melhor entendimento, considere a imagem abaixo, em que: b é a menor base, B é a maior base e h é a altura do trapézio.

O cálculo da fórmula da área do trapézio leva em conta a Base Média, obtida pela seguinte fórmula:
Base Média = (B+b) / 2
Após a determinação da base média, pode-se determinar a área do trapézio com a multiplicação:
Base média x Altura = Atrapézio (B+b)h / 2 = Atrapézio
Como calcular a área do trapézio?
Para demonstrar a aplicação dos cálculos, vamos descobrir juntos a área dos trapézios abaixo. Não esqueça, também, de classificar o polígono conforme ensinado neste artigo.

Para o trapézio A, temos que:
Base Média = (B + b) / 2 => Base Média = (5 + 7 ) / 2 => Base Média = 6
Assim, se Área do trapézio = altura.base média, então:
Atrapézio=4.6=24 cm²
Caso queira, você pode usar as duas fórmulas juntas, de forma que:
(B+b)h / 2 = Atrapézio (5 + 7 ) . 4/ 2 = 24 cm²
Quanto à classificação, o trapézio A não possui indicativos de que os lados não paralelos sejam iguais, e nenhum de seus ângulos é 90º. Dessa forma, o trapézio A é escaleno.
Lembre-se sempre de analisar as unidades de medida apresentadas nas questões!
A partir de agora, usaremos a fórmula direta de Área para o Trapézio, para simplificar as operações.
Para o trapézio B, temos que:
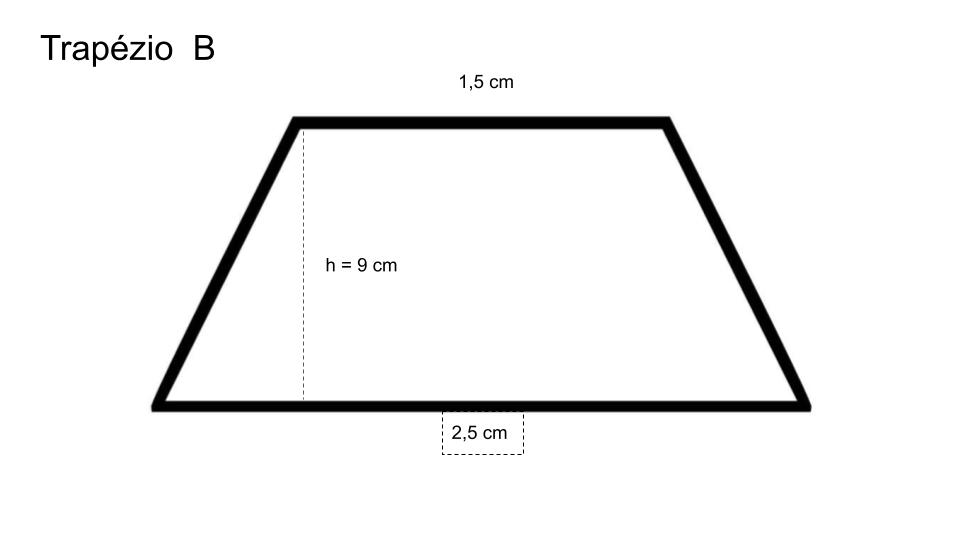
(B+b)h / 2 = Atrapézio => (1,5 + 2,5 ) .9 / 2 = 4 . 9 / 2 = 18 m²
Com relação à classificação, o trapézio B apresenta lados não paralelos iguais. Assim, ele é isósceles.
Para o trapézio C, vemos que:

(B+b)h / 2 = Atrapézio => (8 +7 ).2 / 2 = 15 .2 / 2 = 15 mm²
Note que a figura possui dois ângulos retos (iguais a 90º), então a classificação é a de um trapézio retângulo.
Agora que já estudamos a forma básica de calcular a área trapezóide, considere a questão de vestibular abaixo. Tente resolver o exercício sozinho, e depois analise os conceitos que errou e aqueles que acertou. Assim, você poderá avaliar os pontos fortes e fracos do seu aprendizado até aqui.
Exercícios da área do trapézio em vestibulares
(UNIFESP 2019) A figura representa um trapézio retângulo UNFE de altura UE e uma circunferência de centro P inscrita no triângulo SNF, com S pertencente à UE . Sabe-se que SI é perpendicular a NF , que I é o ponto médio de NF e que UN = 8 cm, EF = 6 cm e ES = 8 cm.
- Calcule NS e a área do trapézio UNFE.
Na figura demonstrativa, os dados apresentados pelo enunciado foram anotados em azul. Depois disso, note a existência de um triângulo retângulo em SEF, e calcule SF pelo teorema de pitágoras (marcado em rosa):
SE² + FE² = FS² => 8²+6²=FS² => 64 + 36 =FS² =>100 =FS² => FS=10 cm
Observe que ISF e NIS são triângulos retângulos que contêm dois lados iguais (x e SI). Após reparar na semelhança, confirme a informação por meio de pitágoras:
SI² + FI² = 10² => SI² + x² = 10² (para ISF)
SI² + NI² = NS² => SI² + x² = NS² (para NIS)
NS² = 10² => NS=10 cm
Por fim, utilizando as relações pitagóricas descubra a medida de US.
US² + NU² = NS² => US²+8²=10² => US² = 100 – 64 => US² = 36 => US=6 cm
Agora que já temos as medidas de todos lados, calcule a área do trapézio:
B=NU= 8cm
b=FE=6 cm
h=US+SE=14cm
(B+b)h / 2 = Atrapézio => (8 +6 ) 14 / 2 =14 .14 / 2 = 98 cm²
Gostou do nosso conteúdo? Então não deixe de conhecer nosso site e tornar-se aluno da Estratégia Vestibulares! Nossos cursos são pensados de forma personalizada para cada vestibular do país. Clique no banner e descubra!
Veja também:
- Geometria: o que é e como é classificada
- Figuras Geométricas: planas, espaciais e como aparece nos vestibulares
- Geometria Plana no Enem: conceito e definições
- Triângulos: definição, perímetro, área, classificações
- Semelhança de triângulos
- Círculo e circunferência: conceitos e exercícios
- Geometria analítica: fórmulas, gráficos e equações
- Geometria Espacial: conheça os sólidos e fórmulas




