A Fórmula de De Moivre é utilizada para se realizar operações de potenciação e de radiciação com números complexos.
Vamos ver alguns conceitos iniciais necessários para entender as fórmulas:
Um número complexo é um número de forma , em que
e
é a unidade imaginária. Esse número, se escrito dessa forma está em sua forma algébrica.
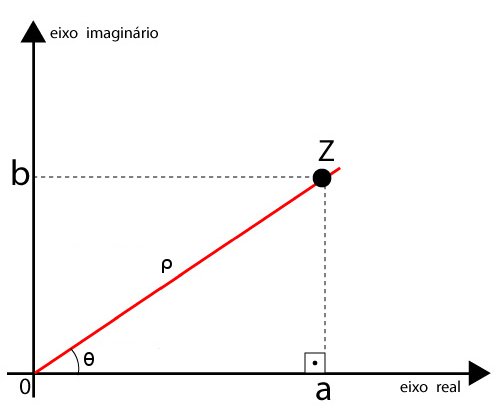
Outra forma de se interpretar os números complexos é exagerá-los como pares ordenados em um plano, o chamado Plano de Argand-Gauss. Nesse plano, colocamos a parte real dos números complexos no eixo das abscissas e a parte imaginária no eixo das ordenadas.
Interpretando os números complexos dessa forma, podemos introduzir a forma trigonométrica dos números complexos, em que eles são dados por , e
pode ser abreviado por
, ou seja,
.
Nessa expressão, temos que, se o número na forma algébrica é dado por , então
é o módulo de z,
e
, em que
) é o argumento de z.
As fórmulas de De Moivre utilizam a forma trigonométrica dos números complexos para realizar operações de potenciação e radiciação.
Navegue pelo conteúdo
Primeira Fórmula de De Moivre
Potenciação
Utiliza-se a primeira fórmula de De Moivre para calcular a n-ésima potência de um número complexo z. Para isso, basta elevar seu módulo à n-ésima potência e multiplicar seu argumento por n.
Segunda Fórmula de De Moivre
Radiciação
A segunda fórmula de De Moivre nos diz que um número complexo z possui n raízes n-ésimas, dadas pela substituição dos valores de k por 0, 1… n-1.
Questão de Vestibular
ITA 2018
As raízes do polinômio , quando representados no plano complexo, formam os vértices de um polígono complexo cuja área é:
a)
b)
c)
d)
e)
Resolução comentada
Vamos, inicialmente, analisar o polinômio dado, para encontrarmos as raízes. Nota-se que, para , o polinômio pode ser visto como uma PG de razão z. Então podemos aplicar a fórmula de soma de PG para a soma
, e obtemos
. Queremos os valores de z para os quais essa expressão é nula, e para isso basta que
.
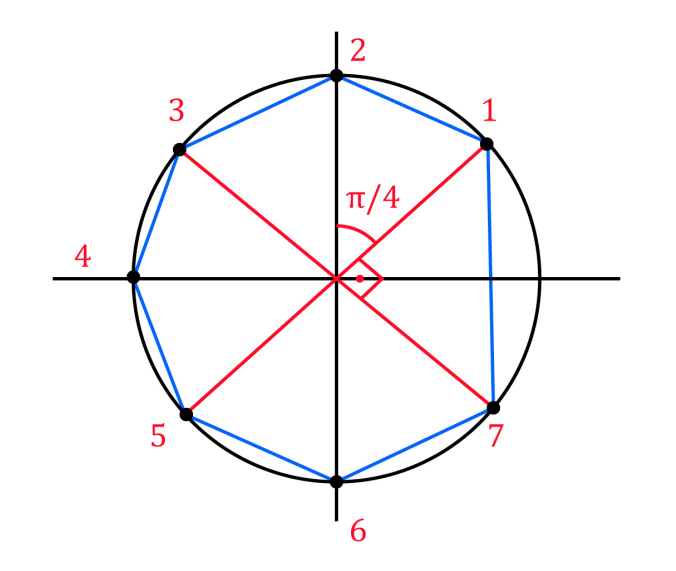
Assim, vemos que as raízes do polinômio são as raízes oitavas de 1, ou seja, .
Vamos aplicar a segunda fórmula de De Moivre, sabendo que o módulo do número real 1 é 1 e seu argumento é 0:
, com
.
Lembrando: supomos inicialmente que , o que exclui o caso
.
Sendo assim, as raízes do polinômio são .
No plano complexo, esses 7 números representam 7 pontos sobre uma circunferência na origem, e estão separados por ângulos de , ou seja:
Para calcular a área desse polígono, basta dividir o polígono: Temos que o
centro da circunferência e os pontos 1 e 2 formam um triângulo de lados 1 e
ângulo central . Assim, podemos calcular a área desse triângulo como
. Podemos formar triângulos idênticos a esse com os pontos 2 e 3, 3 e 4, 4 e 5, 5 e 6, 6 e 7, ressaltando em 6 triângulos com o mesmo valor de área.
Resta, ainda, o triângulo formado pelos pontos 1 e 7, que formam um triângulo retângulo. Então, sua área é .
A área total do polígono será, então, .
Demonstração
Para demonstrar a primeira fórmula de De Moire, usaremos uma indução. Seja . Vamos analisar o que ocorre para
:
Das fórmulas de arcos duplos, sabemos que e
. Assim,
.
Suponha que, para um certo k, . Analisemos
:
Das fórmulas de soma de arcos:
e
vemos que:
. Então:
, o que conclui a demonstração.
Tendo demonstrado a primeira fórmula de De Moivre, podemos usá-la para demonstrar a segunda:
Suponha que e
, tal que
. Então, temos que:
. Aplicando a primeira fórmula de De Moivre para
:
. A igualdade na forma trigonométrica implica que:
e
,
. Precisamos lembrar que a igualdade entre as funções trigonométricas não implica em igualdade direta entre os ângulos, pois as funções são periódicas. Ou seja:
. Como os argumentos dos números complexos são definidos no intervalo
, só faz sentido tomar os valores de k até n-1, já que para k = n o argumento superaria
.
Assim:
, para k = 0,1, …, n-1.
As fórmulas de De Moivre foram nomeadas em homenagem a Abraham De Moivre, matemático francês com diversos estudos relacionados não só aos números complexos, mas também à trigonometria e à estatística.
Por conta de conflitos na França referentes a perseguições religiosas, De Moivre deixou a França em 1685 e foi para a Inglaterra, onde se tornou membro da Royal Society e continuou a desenvolver seus estudos, principalmente na área de análise de riscos e expectativas.