Semelhança de triângulos

Semelhança de triângulos é uma técnica simples. Além de resolver problemas que são aplicações diretas deste assunto, ela pode ajudar bastante no desenvolvimento de questões mais complicadas de geometria plana.

Assim, é importante saber quando dois triângulos podem ser considerados semelhantes e que informações úteis podemos tirar disso, portanto o Estratégia Vestibulares preparou esse artigo para te ajudar!

Navegue pelo conteúdo

No que consiste a semelhança de triângulos?

Dois triângulos são ditos semelhantes se possuírem os três ângulos congruentes e cada par de lados homólogos possuírem a mesma proporção.

Sendo que, lados homólogos são os dois lados que são opostos a ângulos iguais, cada um em um triângulo. Além disso, a notação para dois triângulos semelhantes é o símbolo “~”.

No exemplo abaixo, $\large \Delta ABC \sim \Delta DEF$ se, e somente se,

\large \left\{\begin{matrix} \widehat{A}=\widehat{D} & & \\ \widehat{B}=\widehat{E} & & \\ \widehat{C}=\widehat{F} & & \end{matrix}\right.

\large \frac{\overline{AB}}{\overline{DE}}=\frac{\overline{AC}}{\overline{DF}}=\frac{\overline{BC}}{\overline{EF}}=k

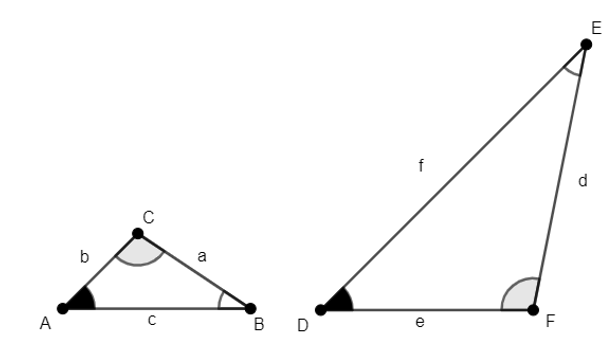
A razão k é chamada de razão de semelhança. Observe que se k for igual a 1, então os dois triângulos são congruentes.

Teorema Fundamental da Semelhança

Se tivermos uma reta paralela a um dos lados de um triângulo e que intercepta os outros dois lados, então a reta determina um triângulo semelhante ao original. No caso abaixo a reta paralela a $\large \overline{AB}$ intercepta os outros dois lados em D e E e então $\large \Delta DEC \sim \Delta ABC$

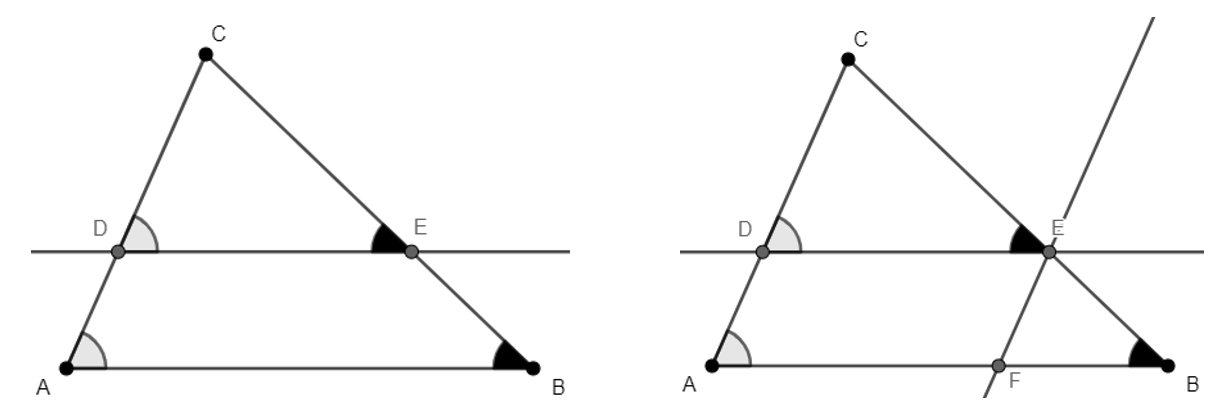
Esse teorema é provado por paralelismo e pelo teorema de Tales. Pois, por paralelismo temos que $\widehat{D}=\widehat{A}$ e $\widehat{E}=\widehat{B}$ , pelo teorema de Tales, temos que $\frac{\overline{CD}}{\overline{CA}}=\frac{\overline{CE}}{\overline{CB}}$ . Além disso, traçamos por E uma paralela a AC. Assim, o paralelogramo ADEF nos dá que $\overline{DE}=\overline{AF}$ , e novamente pelo teorema de Tales, temos que $\frac{\overline{CE}}{CB}=\frac{\overline{AF}}{\overline{AB}}$ . Assim, temos que além dos triângulos terem os três ângulos iguais, $\frac{\overline{CD}}{\overline{CA}}=\frac{\overline{CE}}{\overline{CB}}=\frac{\overline{DE}}{\overline{AB}}$ , ou seja, os triângulos são semelhantes.

Dica forte

Por esse teorema, vemos que ter retas paralelas nos problemas, pode ser uma boa indicação para usar semelhanças de triângulos na resolução.

Casos de semelhança de triângulos

Como geralmente nas questões temos poucas informações acerca dos lados e dos ângulos do triângulo, os casos abaixo vão nos ajudar a identificar triângulos semelhantes.

Caso AA (Ângulo, Ângulo):

Se dois triângulos possuem dois ângulos iguais, então eles são semelhantes. Lembrando que para saber quais lados são proporcionais, sempre olhamos a qual ângulo cada lado está oposto.

Caso LAL (Lado, Ângulo, Lado):

Se já soubermos que entre dois triângulos há dois pares de lados homólogos com a mesma proporção, e os ângulos entre os dois lados de cada um dos triângulos forem iguais, então os triângulos são semelhantes. Como esse caso é mais confuso, a figura abaixo ajuda a entendê-lo.

Se $\left\{\begin{matrix} \frac{\overline{AB}}{\overline{AE}}=\frac{\overline{AC}}{\overline{DF}} & & \\ \\ \widehat{A}=\widehat{D} & & \end{matrix}\right.$ , então $\Delta ABC\sim \Delta DEF$ .

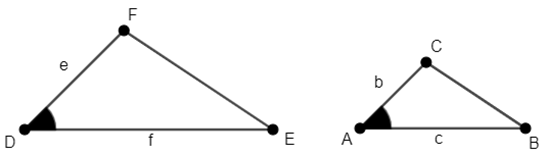
Caso LLL (Lado, Lado, Lado):

Se um triângulo possui os três lados proporcionais aos três lados de um outro triângulo com a mesma razão, então esses triângulos são semelhantes.

Propriedades

A semelhança de triângulos é reflexiva, simétrica e transitiva. Por reflexiva, entendemos que um triângulo é semelhante a si mesmo.

Por simétrica, se um triângulo é semelhante a um outro, este segundo é semelhante ao primeiro. Já por transitiva, se $\Delta ABC\sim \Delta DEF$ e $\Delta DEF \sim \Delta GHI$ , então $\Delta ABC\sim \Delta GHI$ .

Portanto, podemos conseguir com um dos casos mencionados acima descobrir que dois triângulos são semelhantes, e com outro caso provar que um dos triângulos é semelhante a um terceiro.

Assim, conseguimos demonstrar que dois triângulos são semelhantes mesmo que os dois não tenham informações em comum o suficiente para se encaixar em algum dos casos.

Como cai Semelhança de Triângulos no vestibular?

Uma boa tática para resolver questões é “fazer aparecer” semelhança de triângulos através de alguma construção, como traçar uma paralela. Por isso, é sempre bom, inicialmente, desenhar a figura quando for questões de geometria plana. A questão abaixo, do vestibular do ITA, exemplifica isso.

Questão ITA 2014

Se um triângulo isósceles ABC , cuja área mede $48cm^{2}$ , a razão entre as medidas da altura $\overline{AP}$ e da base $\overline{BC}$ é igual a $\frac{2}{3}$ . Das informações abaixo:

I – As medianas relativas aos lados $\overline{AB}$ e $\overline{AC}$ medem $\sqrt{97}cm$ ;
II – O baricentro dista 4cm do vértice ;
III – Se $\alpha$ é o ângulo formado pela base $\overline{BC}$ com a mediana $\overline{BM}$ , relativa ao lado $\overline{AC}$ , então $cos\alpha =\frac{3}{\sqrt{97}}$ ,

é(são) verdadeira(s)

A ( ) apenas I.

B ( ) apenas II.

C ( ) apenas III.

D ( ) apenas I e III.

E ( ) apenas II e III.

Resolução Comentada

Com as informações do enunciado podemos construir a figura abaixo. Note que se $\overline{AP}=8x$ , então, pela razão dada, $\overline{BC}=12x$ . Como o triângulo é isósceles, então a mediana $\overline{AP}$ é, também, altura.

Assim, através da área do triângulo, podemos calcular o valor de x:

\left[ABC\right]=\frac{\left(8x\right)\left(12x\right)}{2}=48cm^2\Rightarrow x=1cm

Uma boa construção a se fazer para esse problema, é a perpendicular a $\overline{BC}$ partindo de , sendo o ponto médio de $\overline{AC}$ . Isso porque podemos calcular o valor da mediana $\overline{BM}$ por Pitágoras se tivermos o valor de $\overline{MD}$ . E é aí que entra a semelhança de triângulos.

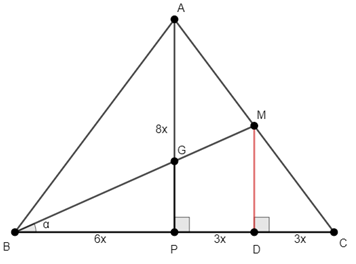
Os triângulos CDM e CPA são semelhantes (caso AA) e como $\overline{AC}=2\ \overline{CM}$ então $\overline{MD}=\frac{\overline{AP}}{2}=\frac{8x}{2}=4x=4cm$ .

Além disso,

\overline{CD}=\frac{\overline{PC}}{2}=\frac{6x}{2}=3x=3cm\Rightarrow

\overline{BD}=\overline{BC}-\overline{CD}=12x-2x=9x=9cm

De forma análoga, a mediana $\overline{CN}=\sqrt{97}cm$ . Assim, o item I é verdadeiro.

Aplicando agora a semelhança de triângulos nos triângulos BPG e BDM (caso AA), temos que

\frac{\overline{GP}}{\overline{MD}}=\frac{6x}{9x}\Rightarrow\overline{GP}=\frac{8}{3}cm\Rightarrow\overline{AG}=8cm-\frac{8}{3}cm=\frac{16}{3}cm

Assim, o item II é falso.

Por fim, $cos\alpha=\frac{\overline{BD}}{\overline{BM}}=\frac{9}{\sqrt{97}}$ , ou seja, o item III também é falso. Assim, a resposta da questão é o item A.

Essa questão poderia ser resolvida sem a construção de $\overline{MD}$ , e sem utilizar semelhança de triângulos, entretanto, dessa maneira, a questão acaba saindo mais rápido pois as contas ficaram bem mais simples. Assim, vemos que a semelhança de triângulos é um artifício muito bom na resolução de questões, mas é necessário que você treine mais um pouco para pegar o jeito e conseguir enxergar os triângulos que são semelhantes em uma questão.

Semelhança de triângulos

No que consiste a semelhança de triângulos?