Gabarito UEL 2020 – Matemática – Resolução Comentada

Olá, pessoal… Tudo bem? Sou a prof. Marçal, do Estratégia Vestibulares, e escrevo este artigo para lançar o Gabarito UEL 2020, da disciplina de Matemática. Nesta página, você vai conferir a resolução comentada completa. Vamos nessa??

">Resolução Matemática – Vestibular UEL 2020" class="wp-block-file__button" download>Baixar

UEL 2020

Questão 10

A icônica obra Mona Lisa, de Leonardo Da Vinci, exposta no Museu do Louvre, possibilita pôr à prova as proporções matemáticas nela presentes. Partindo de um quadrado $\dpi{100} \large ABCD$ de lado 1, que delimita uma região abaixo da cabeça, pode-se obter um retângulo, que contém a cabeça da Mona Lisa, por meio da construção geométrica descrita a seguir.

Seja O o ponto médio do segmento $\dpi{100} \large \overline{AB}$ . Tome a circunferência de centro O e raio $\dpi{100} \large \overline{OD}$ . Encontre o ponto $\dpi{100} \large E$ dado pela intersecção da circunferência com a semirreta $\dpi{100} \large \overrightarrow{BA}$ . Considere o ponto $\dpi{100} \large F$ de modo a obter o retângulo de vértices $\dpi{100} \large EADF$ , como ilustrado na figura a seguir.

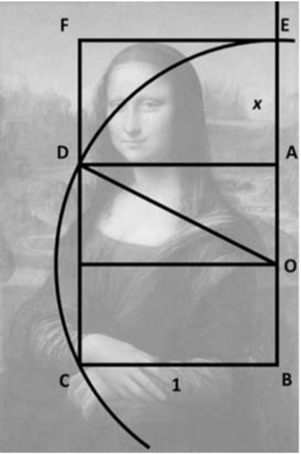
Com base na construção geométrica fornecida e na figura, assinale a alternativa que apresenta, corretamente, o comprimento do segmento $\dpi{100} \large \overline{EA}$ .

a) $\dpi{100} \large \frac{1-\sqrt{5}}{2}$

b) $\dpi{100} \large \frac{3-\sqrt{5}}{2}$

c) $\dpi{100} \large \frac{\sqrt{5}-1}{2}$

d) $\dpi{100} \large \frac{\sqrt{5}+1}{2}$

e) $\dpi{100} \large \frac{\sqrt{5}+3}{2}$

Resolução Comentada

Com O é o ponto médio de $\dpi{100} \large \overline{AB}$ e $\dpi{100} \large AB=1$ , temos que $\dpi{100} \large \overline{AO}=\frac{1}{2}$ .

Considerando o ponto G como médio entre $\dpi{100} \large \overline{CD}$ , temos que $\dpi{100} \large \overline{CD}=1$ e $\dpi{100} \large \overline{DG}=\overline{AO}=\frac{1}{2}$ .

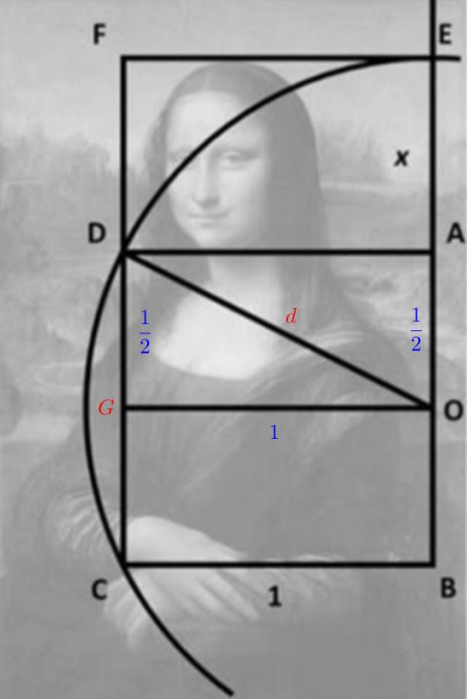
Dessa forma, podemos calcular, utilizando o teorema de Pitágoras, a distância $\dpi{100} \large d=\overline{OD}$ que será igual ao raio da circunferência traçada.

$\dpi{100} \large d^2=1^2+\left(\frac{1}{2}\right)^2$

$\dpi{100} \large d^2=1+\frac{1}{4}$

$\dpi{100} \large d^2=\frac{5}{4}$

$\dpi{100} \large \sqrt{d^2}=\sqrt{\frac{5}{4}}$

$\dpi{100} \large \left|d\right|=\frac{\sqrt5}{2}$

$\dpi{100} \large d=\pm\frac{\sqrt5}{2}$

Como estamos lidando com o raio de uma circunferência, podemos descartar a parte negativa e considerar

$\dpi{100} \large d=\frac{\sqrt5}{2}$

Tomando $\dpi{100} \large d=\frac{\sqrt5}{2}$ como o raio da circunferência, podemos dizer que $\dpi{100} \large \overline{OD}=\overline{OE}=d=\frac{\sqrt5}{2}$ . Como $\dpi{100} \large \overline{OE}=\overline{OA}+\overline{AE}$ , temos:

$\dpi{100} \large \overline{OE}=\overline{OA}+\overline{AE}$

$\dpi{100} \large \frac{\sqrt5}{2}=\frac{1}{2}+x$

$\dpi{100} \large \frac{\sqrt5}{2}-\frac{1}{2}=x$

$\dpi{100} \large \frac{\sqrt5-1}{2}=x$

Gabarito: C

Questão 30

Analise a figura a seguir.

Utilizando duas retas graduadas e perpendiculares, um estudioso caracteriza cada ponto da obra de Johannes Vermeer, como um par ordenado no plano cartesiano, de forma que um ponto no brinco de pérola esteja associado à origem (0,0). De acordo com a associação feita, o estudioso constata que os pontos de coordenadas (-10,0) e (-8,8) se localizam, respectivamente, na boca e no olho retratados.

Assinale a alternativa que apresenta, corretamente, uma propriedade da parábola que passa pelos três pares ordenados presentes no texto.

a) Tem por equação $\dpi{100} \large y\ +\ x^2+\ 5x=0$

b) Tem concavidade voltada para cima.

c) Tem por vértice um ponto na região do ombro retratado.

d) Tem por equação $\dpi{100} \large 2y\ +\ x^2+\ 10x=0$

e) Admite três raízes reais distintas, todas localizadas no turbante.

Resolução Comentada

Antes de julgarmos as alternativas, vamos explicitar os três pontos citados no enunciado.

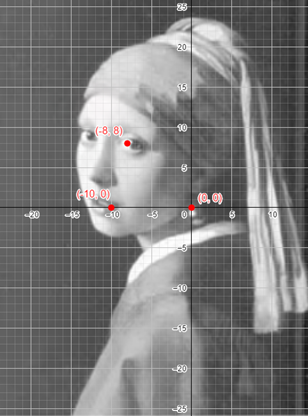
Antes mesmo de calcularmos qual parábola pode conter esses três pontos, podemos perceber que ela terá concavidade negativa, pela disposição dos pontos.

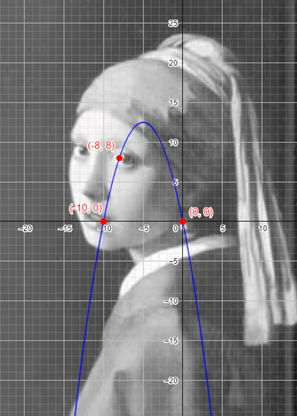
Só por isso, já podemos descartar as alternativas b) e c).

Por ser uma parábola, podemos ter até duas raízes, ou seja, já podemos descartar a alternativa e) também.

Sobram as alternativas a) e d) para encontrarmos a equação da parábola. Como ambas apresentam concavidade negativa, não podemos excluir uma ou outra por esse motivo.

Vamos, então, calcular a equação da parábola que passa por esses três pontos.

Substituindo os pontos (0,0), (-10,0) e (-8,8) na equação $\dpi{80} y=ax^2+bx+c$ , obtemos o seguinte sistema linear:

$\dpi{80} \left\{\begin{matrix}0=a\cdot0^2+b\cdot0+c\\\ \\0=a\left(-10\right)^2+b\left(-10\right)+c\\\ \\8=a\left(-8\right)^2+b\left(-8\right)+c\\\end{matrix}\right.\rightarrow$

$\dpi{80} \left\{\begin{matrix}0=c\\\ \\0=100a-10b+c\\\ \\8=64a-8b+c\\\end{matrix}\right.\rightarrow$

$\dpi{80} \left\{\begin{matrix}0=c\\\ \\0=100a-10b\\\ \\8=64a-8b\\\end{matrix}\right.\rightarrow$

$\dpi{80} \left\{\begin{matrix}0=c\\\ \\b=10a\\\ \\8=64a-8b\\\end{matrix}\right.\rightarrow$

$\dpi{80} \left\{\begin{matrix}0=c\\\ \\b=10a\\\ \\8=64a-8\cdot10a\\\end{matrix}\right.\rightarrow$

$\dpi{80} \left\{\begin{matrix}0=c\\\ \\b=10a\\\ \\8=-16a\\\end{matrix}\right.\rightarrow$

$\dpi{80} \left\{\begin{matrix}0=c\\\ \\b=10a\\\ \\-\frac{1}{2}=a\\\end{matrix}\right.\rightarrow$

$\dpi{80} \left\{\begin{matrix}0=c\\\ \\b=10\cdot\left(-\frac{1}{2}\right)\\\ \\-\frac{1}{2}=a\\\end{matrix}\right.\rightarrow$

$\dpi{80} \left\{\begin{matrix}0=c\\\ \\b=-5\\\ \\-\frac{1}{2}=a\\\end{matrix}\right.$

Dessa forma, conseguimos nossa equação da parábola, veja:

$\dpi{80} y=ax^2+bx+c$

$\dpi{80} y=-\frac{1}{2}\cdot x^2-5\cdot x+0$

$\dpi{80} 2y=-1\cdot x^2-10\cdot x$

$\dpi{80} 2y+1\cdot x^2+10\cdot x=0$

Gabarito: D

Questão 39

Na exposição virtual “A Beleza da Matemática”, realizada no Museu do Amanhã, o belo é celebrado como simetria matemática, como exemplificado na imagem a seguir.

No plano cartesiano, dois pontos distintos P e Q são simétricos em relação a uma reta r se as seguintes condições forem simultaneamente atendidas:

I) a distância de P a r é igual à distância de Q a r
II) a reta que contém P e Q é perpendicular à reta r

Suponha que, no plano que contém a imagem da borboleta, o eixo de simetria r seja dado pela equação de reta $\dpi{80} y+x=2$ . Se $\dpi{80} P=(-2,0)$ é um ponto desse plano, assinale a alternativa que apresenta, corretamente, o ponto simétrico a P em relação à reta r.

a) (0,2)
b) (2,0)
c) (2,2)
d) (2,4)
e) (4,2)

Resolução Comentada

Apesar de não ser estritamente necessário, vamos explicitar a reta y+x=2 e o ponto P=(-2,0) na imagem da borboleta.

Nessa situação, o ponto P’, simétrico a P, estará à mesma distância de P a r, mas “do outro lado” da reta r.

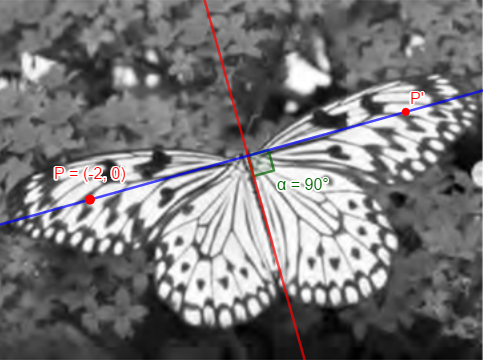
Dessa forma, podemos dizer que a distância de P a r é igual à distância de P’ a r.

Tanto P quanto P’ pertencem a uma reta s que é perpendicular à reta r e que passa por P.

Vamos, então, retirar a figura da borboleta e trabalhar apenas no plano cartesiano com as coordenadas e equações conhecidas.

Nossa reta r, eixo de simetria, é dada por y+x=2. Quando x=0, temos y+0=2, o que resulta em y=2 como nosso intercepto-y.

Colocando os pontos P e P’, além de o intercepto-y e os eixos coordenados, temos um esboço como o que segue.

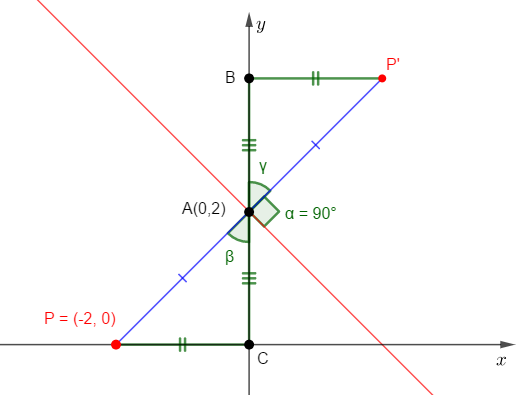
Perceba que os triângulos APC e ABP’ são congruentes, o que nos permite equacionar

Desse modo, as coordenadas do ponto P’ são dadas por:

$\dpi{80} x_p=P^\prime B=2$

$\dpi{80} y_p=AB+AC=2+2=4$

Assim, temos que: $\dpi{80} P^\prime=\left(x_p,y_p\right)=\left(2,4\right)$ .

Gabarito: D

Questão 40

Uma característica fundamental do plano corpóreo de um animal é sua forma geral e um aspecto básico dessa forma é a simetria. O termo simetria refere-se ao arranjo regular das estruturas corporais em relação ao eixo do corpo. Os animais que podem ser divididos ao longo de ao menos um plano, de modo que as metades resultantes sejam semelhantes entre si, são conhecidos como simétricos.

Com base nas informações apresentadas, considere as afirmativas a seguir.

I. Um corpo com simetria bilateral tem a forma geral de um cilindro, com um eixo principal ao redor do qual as diversas partes do corpo estão dispostas.

II. Na simetria bilateral, um lado do corpo difere do outro por uma escala distinta de 1, fazendo com que as áreas, em cada lado, se alterem nessa mesma escala.

III. É vantajoso para um animal com simetria radial, pelo seu estilo de vida, ser capaz de interagir com o ambiente igualmente a partir de várias direções.

IV. O volume do corpo de um animal, que admite simetria bilateral exata, é igual ao dobro do volume de qualquer um de seus dois lados.

Assinale a alternativa correta.

a) Somente as afirmativas I e II são corretas.

b) Somente as afirmativas I e IV são corretas.

c) Somente as afirmativas III e IV são corretas.

d) Somente as afirmativas I, II e III são corretas.

e) Somente as afirmativas II, III e IV são corretas.

Resolução Comentada

O enunciado, apesar de explicar o que é uma simetria, deixa o termo “bilateral” apenas nas afirmativas, o que pode causar alguma confusão.

O termo bilateral faz relação às duas partes simétricas, duas metades.

Esclarecido o termo, vamos julgar as alternativas.

I. Um corpo com simetria bilateral tem a forma geral de um cilindro, com um eixo principal ao redor do qual as diversas partes do corpo estão dispostas.

Falsa, o corpo não precisa ter a forma de um cilindro para ser simétrico. Pense na borboleta presente no exercício anterior, ela é simétrica, mas não é cilíndrica.

II. Na simetria bilateral, um lado do corpo difere do outro por uma escala distinta de 1, fazendo com que as áreas, em cada lado, se alterem nessa mesma escala.

Falsa, o corpo é dividido em duas metades, ou seja, as partes, até onde possível, são simétricas, correspondentes, são de mesmo tamanho, apenas em uma disposição simétrica, “oposta”. A escala de uma para a outra é, exatamente, 1.

III. É vantajoso para um animal com simetria radial, pelo seu estilo de vida, ser capaz de interagir com o ambiente igualmente a partir de várias direções.

Essa alternativa aborda conceitos da Biologia, então, com a palavra, a professora Bruna Klassa, professora de Biologia do Estratégia Vestibulares.

“A simetria radial é aquela em que o corpo do animal pode ser dividido em vários planos iguais dispostos em torno de um eixo longitudinal. Em face dessa característica, não podemos afirmar que eles possuem região dorsal e ventral, lado esquerdo e direito ou cabeça e cauda. Animais com esse tipo de simetria recebem o nome de radiados e são representados pelos cnidários e equinodermos adultos. A simetria radial é uma vantagem, especialmente, mas não exclusivamente, para a existência séssil (aqueles que se mantém fixos ao substrato), pois permite que o animal responda aos desafios do seu ambiente a partir de todas as direções. “

IV. O volume do corpo de um animal, que admite simetria bilateral exata, é igual ao dobro do volume de qualquer um de seus dois lados.

Correta, se o corpo é dividido em duas partes simétricas “iguais”, ou seja, duas metades, o corpo inteiro tem o dobro do volume de cada uma de suas metades. Aliás, é exatamente esse o conceito de metade, não?

Gabarito: C

Questão 42

Muitas formas presentes na natureza são de difícil representação por entes geométricos tradicionais, como retas, planos e cubos, mas que podem ser aproximadas por meio da aplicação de operações geométricas sucessivas.

Por exemplo, certos animais filtradores, como as esponjas, possuem esqueleto flexível de espongina, que podem ter sua forma aproximada pela n-ésima etapa da construção da região denominada Esponja de Menger, cujo volume V(n) é dado por:

$\dpi{80} V\left(n\right)=\left(\frac{20}{27}\right)^{n-1}-7\cdot{20}^{n-1}\cdot\left(\frac{1}{27}\right)^n,\ para\ n\in\mathbb{N}^\ast$

Na sequência, estão ilustrados um esqueleto flexível de espongina, um cubo unitário e as três primeiras etapas da construção da Esponja de Menger, como apresentado na exposição “A Beleza da Matemática” do Museu do Amanhã.

Com base nas informações apresentadas, considere as afirmativas a seguir.

I. As esponjas pertencem ao filo Cnidaria e apresentam, como característica, a presença de um tipo básico de indivíduo denominado pólipo.

II. O volume de cada etapa da construção da Esponja de Menger é menor que o volume da etapa anterior, isto é, $\dpi{80} V(n\ +\ 1)<v(n)$ para todo n e $\dpi{80} N^\ast$ .

III. Independentemente de qual etapa da construção da Esponja de Menger seja considerada, seu volume é um número racional.

IV. Além da espongina, a estrutura esquelética das esponjas é constituída por colágeno fibrilar, uma proteína, e espículas silicosas ou calcáreas.

Assinale a alternativa correta.

a) Somente as afirmativas I e II são corretas.

b) Somente as afirmativas I e IV são corretas.

c) Somente as afirmativas III e IV são corretas.

d) Somente as afirmativas I, II e III são corretas.

e) Somente as afirmativas II, III e IV são corretas.

Resolução Comentada

Vamos analisar alternativa a alternativa.

I. As esponjas pertencem ao filo Cnidaria e apresentam, como característica, a presença de um tipo básico de indivíduo denominado pólipo.

Novamente, conceitos biológicos são necessários. Assim, invoquemos novamente a professora Bruna Klassa.

“A afirmativa I é falsa, porque as esponjas são animais que pertencem ao filo Porifera. Os cnidários são representados pelas anêmonas, águas-vivas e corais, e eles sim apresentam uma fase de pólipo (assexuada) e uma fase de medusa (sexuada), caracterizando um ciclo de vida marcado pela alternância de gerações.”

II. O volume de cada etapa da construção da Esponja de Menger é menor que o volume da etapa anterior, isto é, $\dpi{80} V(n\ +\ 1)<v(n)$ para todo n e $\dpi{80} N^\ast$ .

Pela própria construção da esponja, já temos a impressão de a premissa ser verdadeira, afinal, vamos, a cada etapa da construção da esponja de Menger, retirando uma parte do volume da esponja anterior. No entanto, para termos certeza, façamos a análise a partir da premissa e vejamos se chegamos em uma verdade.

$\dpi{80} V(n\ +\ 1)<v(n)$

$\dpi{100} \left(\frac{20}{27}\right)^{n\ +\ 1-1}-7\cdot{20}^{n\ +\ 1-1}\cdot\left(\frac{1}{27}\right)^{n\ +\ 1}<\left(\frac{20}{27}\right)^{n-1}-7\cdot{20}^{n-1}\cdot\left(\frac{1}{27}\right)^n$

$\dpi{80} \large \left(\frac{20}{27}\right)^{n\ }-7\cdot{20}^{n\ }\cdot\left(\frac{1}{27}\right)^{n\ +\ 1}<\left(\frac{20}{27}\right)^{n-1}-7\cdot{20}^{n-1}\cdot\left(\frac{1}{27}\right)^n$

$\dpi{80} \large \left(\frac{20}{27}\right)^{n\ }-\left(\frac{20}{27}\right)^{n-1}<7\cdot{20}^{n\ }\cdot\left(\frac{1}{27}\right)^{n\ +\ 1}-7\cdot{20}^{n-1}\cdot\left(\frac{1}{27}\right)^n$

$\dpi{80} \large \left(\frac{20}{27}\right)^{n-1}\cdot\left[\frac{20}{27}-1\right]<7\cdot{20}^{n-1}\cdot\left(\frac{1}{27}\right)^n\left[20\cdot\left(\frac{1}{27}\right)^1-1\right]$

$\dpi{80} \large \left(\frac{20}{27}\right)^{n-1}\cdot \cancel {\left [ - \frac{7}{27} \right ]}<7\cdot{20}^{n-1}\cdot\left(\frac{1}{27}\right)^n\cancel {\left [ - \frac{7}{27} \right ]}$

7\cdot\frac{{20}^n}{{20}^1}\cdot\left(\frac{1}{27}\right)^n” alt=”\dpi{80} \left(\frac{20}{27}\right)^{n-1}>7\cdot\frac{{20}^n}{{20}^1}\cdot\left(\frac{1}{27}\right)^n” align=”absmiddle”>

7\cdot\frac{1}{{20}^1}\cdot\left(\frac{20}{27}\right)^n” alt=”\dpi{80} \left(\frac{20}{27}\right)^{n-1}>7\cdot\frac{1}{{20}^1}\cdot\left(\frac{20}{27}\right)^n” align=”absmiddle”>

\frac{7}{20}\cdot\cancel{\left&space;(&space;\frac{20}{27}&space;\right&space;)^{n}}” alt=”\dpi{80} \large \cancel{\left ( \frac{20}{27} \right )^{n}}\cdot\left(\frac{20}{27}\right)^{-1}>\frac{7}{20}\cdot\cancel{\left ( \frac{20}{27} \right )^{n}}” align=”absmiddle”>

\frac{7}{20}” alt=”\dpi{80} \large \frac{27}{20}>\frac{7}{20}” align=”absmiddle”>

7″ alt=”\dpi{80} \large 27>7″ align=”absmiddle”>

Como a desigualdade a que chegamos retrata uma verdade, podemos tomar nossa premissa de que V(n + 1)<V(n) como válida, como esperávamos. Dessa forma, premissa verdadeira.

III. Independentemente de qual etapa da construção da Esponja de Menger seja considerada, seu volume é um número racional.

Perceba que não há, na equação de V\left(n\right), indicação alguma de que a expressão do segundo membro resulte em um número irracional: uma raiz, um número irracional qualquer…

Na verdade, é bem o contrário, toda a expressão é construída com frações, já que os valores de n são sempre positivos, resultando em potências sempre naturais.

Premissa verdadeira.

IV. Além da espongina, a estrutura esquelética das esponjas é constituída por colágeno fibrilar, uma proteína, e espículas silicosas ou calcáreas.

E, com a palavra, mais uma vez, nossa convidada ilustre, Professora Bruna Klassa… Já já ela perde a paciência conosco!

“A afirmativa IV é verdadeira. As esponjas são classificadas conforme o tipo de espícula que apresentam. Esponjas com espículas de espongina pertencem à Classe Demospongiae e representam a maior parte da diversidade desses animais. Esponjas com espículas silicosas pertencem à classe Hexactinellida e esponjas com espículas calcáreas pertencem à classe Calcarea.”

Gabarito: E

Questão 47

Um estudante decide pôr à prova a frase “vida é código e combinação”. Sabendo que os indivíduos de uma determinada espécie apresentam um DNA com exatos 150 milhões de bases nitrogenadas em cada cadeia, o estudante cria um programa para gerar, aleatoriamente, uma sequência de 150 milhões de letras que serão sorteadas honestamente dentre A, C, G e T.

Fixada uma cadeia do DNA de um determinado indivíduo desta espécie, assinale a alternativa que apresenta, corretamente, a probabilidade de esse programa gerar uma sequência que represente essa cadeia do DNA.

a) $\dpi{80} 2^{-3x{10}^7}$

b) $\dpi{80} 2^{-3x{10}^8}$

c) $\dpi{80} 4^{-3x{10}^8}$

d) $\dpi{80} {60}^{-1}x{10}^{-7}$

e) $\dpi{80} {60}^{-1}x{10}^{-8}$

Resolução Comentada

O enunciado nos deu um comando interessante: “Fixada uma cadeia do DNA de um determinado indivíduo desta espécie…”.

Esse comando nos diz que não devemos considerar as duas cadeias do DNA e sim uma cadeia apenas. Fixada essa cadeia, qual a probabilidade de gerá-la com o programa?

Dessa forma, uma cadeia com 150 milhões de bases dentre A, C, G e T será algo como:

$\dpi{80} \underbrace{ATCGTTTCAGCTAAACATGGGGAT}_{150\ milhoes\ de\ termos}$

Pelo princípio multiplicativo, podemos dizer que temos quatro opções para escolher a primeira base nitrogenada da cadeia, A, C, G ou T.

Para escolher a segunda, as mesmas opções, A, C, G ou T.

Dessa forma, a cada base escolhida, quatro opções de escolha, portanto:

$\dpi{80} \underbrace{4\cdot4\cdot4\cdot4\cdot4\cdot4\cdot4\cdot4\cdot4\cdot4\cdot4\cdot4\cdot4\ldots\ }_{150\ milhoes\ de\ termos} =$

$\dpi{80} 4^{150.000.000}=\left(2^2\right)^{150.000.000}=2^{300.000.000}=2^{3\cdot{10}^8}$

Perceba que esse número representa a quantidade de escolhas possíveis, ou seja, todas as possibilidades das bases nitrogenadas nas condições dadas.

A probabilidade de o programa gerar uma em específico é dada pela nossa definição de probabilidade:

$\dpi{80} Probabilidade=\frac{casos\ que\ procuro}{todos\ os\ caos\ possiveis}= \frac{1}{2^{3\cdot{10}^8}}=2^{-3\cdot{10}^8}$

Gabarito: B

Questão 54

Leia o texto e observe a imagem a seguir.

No Brasil, a preservação natural de um cadáver é rara devido ao clima tropical e ao solo ácido, que aceleram a sua decomposição. Por isso, a múmia encontrada em Goianá, Minas Gerais, no século XIX é tão incomum.

Adaptado de: www.museunacional.ufrj.br

Passados t anos após a morte deste ser humano, suponha que a massa m(t) de seu cadáver, medida em quilogramas, seja dada por $\dpi{80} m\left(t\right)=40e^{-C\cdot t}$ , onde $\dpi{80} t\ =\ 600$ anos a múmia possuía exatos 4 kg, assinale a alternativa que apresenta, corretamente, o valor do parâmetro C.

a) $\dpi{80} C=\frac{1}{200}\log_e{50}$

b) $\dpi{80} C=\frac{1}{300}\log_e{20}$

c) $\dpi{80} C=\frac{1}{400}\log_e{30}$

d) $\dpi{80} C=\frac{1}{500}\log_e{40}$

e) $\dpi{80} C=\frac{1}{600}\log_e{10}$

Resolução Comentada

Pelo enunciado, sabemos que passados $\dpi{80} \large t=600$ anos a múmia possuía 4kg, ou seja, $\dpi{80} \large m(600)=4$ . Vamos colocar esses dados na equação fornecida.

$\dpi{80} \large m\left(t\right)=40e^{-C\cdot t}$

$\dpi{80} \large m\left(600\right)=40e^{-C\cdot600}$

$\dpi{80} \large 4=40e^{-C\cdot600}$

$\dpi{80} \large \frac{\cancel4}{\cancel4}=\frac{^{10}\cancel{40}e^{-c.600}}{\cancel4}$

$\dpi{80} \large 1=10e^{-C\cdot600}$

$\dpi{80} \large log1=\log\funcapply(10e^{-C\cdot600})$

$\dpi{80} \large 0=\log{10}+\log\funcapply(e^{-C\cdot600})$

$\dpi{80} \large 0=1-C\cdot600\cdot\log\funcapply(e)$

$\dpi{80} \large C\cdot600\cdot\log\funcapply(e)=1$

$\dpi{80} \large \frac{C\cdot 600\cdot log(e)}{600\cdot log(e)}=\frac{1}{600\cdot log(e)}$

$\dpi{80} \large \frac{C\cancel {\cdot 600\cdot log(e)}}{\cancel{600\cdot log(e)}}=\frac{1}{600\cdot log(e)}$

$\dpi{80} \large C=\frac{1}{600\cdot log(e)}$

$\dpi{80} \large C=\frac{1}{600}\cdot\frac{1}{\log(e)}$

$\dpi{80} \large C=\frac{1}{600}\cdot\log_e{10}$

Gabarito: E

Questão 58

Leia o texto a seguir.

Luzia é de inestimável valor científico por se tratar do mais antigo fóssil humano paleoamericano já encontrado no Brasil. O crânio e ossos da coxa e do quadril de Luzia foram achados em 1975, em uma gruta da região de Lagoa Santa, em Minas Gerais. Seu esqueleto foi datado de 11,5 mil anos e ela deve ter morrido aos 25 anos. Neste século, seu rosto foi reconstituído na Inglaterra.

Adaptado de: www.museunacional.ufrj.br

Um dos processos de datação arqueológica ocorre calculando o porcentual r da quantidade de carbono 14 presente no fóssil em relação à quantidade desse mesmo elemento encontrada em um ser vivo de características semelhantes. Suponha que para fósseis humanos paleoamericanos a figura a seguir exiba o gráfico da função $\dpi{100} f:\mathbb{R}_+^\ast\rightarrow\mathbb{R}_+^\ast$ que associa, a cada r, a quantidade $\dpi{100} t=f\left(r\right)$ de anos que se passaram desde a morte do ser humano em questão.

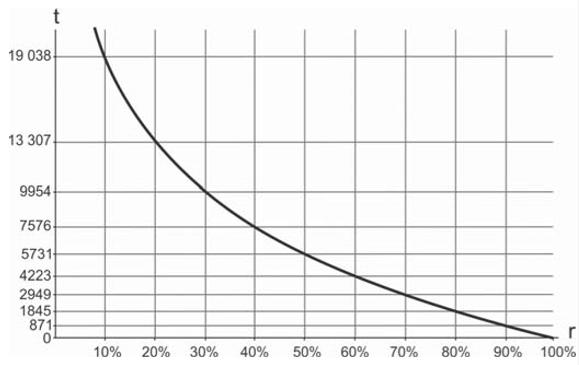
Com base no texto e no gráfico, assinale a alternativa correta.

a) No caso de Luzia, o porcentual r no momento de sua datação se encontrava entre 20% e 30%.

b) À medida que o tempo passa, o porcentual r de um fóssil humano paleoamericano cresce em relação a um ser vivo de características semelhantes.

c) Um fóssil humano paleoamericano, datado entre 2949 e 4223 anos, apresenta porcentual r de, no máximo, 50%.

d) O porcentual r apresentado por Luzia, imediatamente após sua morte, se encontrava entre 80% e 90%.

e) O tempo necessário para que um fóssil humano paleoamericano perca 10 pontos percentuais de r é constante.

Resolução Comentada

Vamos analisar alternativa a alternativa.

a) No caso de Luzia, o porcentual r no momento de sua datação se encontrava entre 20% e 30%.

Verifiquemos a veracidade da informação pelo gráfico, uma vez que não temos a função para analisar algebricamente.

Como, pelo texto, o esqueleto de Luzia foi datado de 11,5 mil anos, analisemos a faixa do eixo t que contém essa idade.

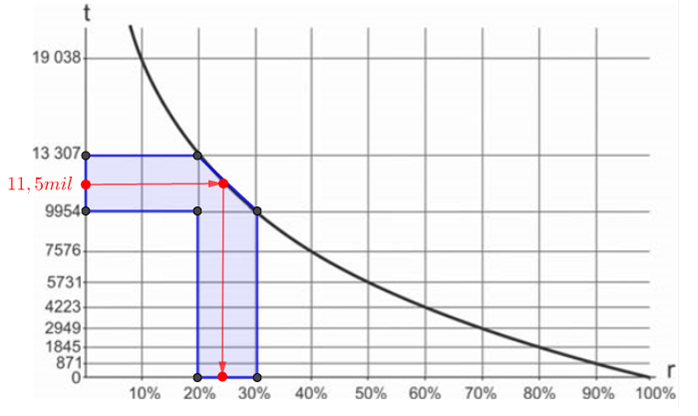
Dessa forma, realmente, a faixa que contém a idade de 11,5 mil anos corresponde a valores de r entre 20% e 30%, portanto, essa alternativa é nosso gabarito.

No intuito de aprendizado, vejamos o que torna inválidas cada uma das outras opções.

b) À medida que o tempo passa, o porcentual r de um fóssil humano paleoamericano cresce em relação a um ser vivo de características semelhantes.

Podemos perceber pelo gráfico que a relação entre r e t são inversamente proporcionais, isto é, enquanto o valor de um deles aumenta, o do outro diminui, portanto, alternativa falsa.

c) Um fóssil humano paleoamericano, datado entre 2949 e 4223 anos, apresenta porcentual r de, no máximo, 50%.

A faixa correspondente ao intervalo entre 2949 e 4223 anos retorna valores de r entre 60% e 70%, superiores aos 50% dados como máximo na alternativa, portanto, alternativa falsa.

d) O porcentual r apresentado por Luzia, imediatamente após sua morte, se encontrava entre 80% e 90%.

Imediatamente após a morte, como podemos ver no gráfico na faixa entre 0 e 871 anos, os valores de r estão compreendidos entre 90% e 100%. Alternativa falsa.

e) O tempo necessário para que um fóssil humano paleoamericano perca 10 pontos percentuais de r é constante.

O gráfico mostra uma curva em que as perdas percentuais não são lineares com relação ao tempo decorrido. Veja como os valores dos intervalos de t são irregulares, enquanto os valores de r são regulares de 10% em 10%. Alternativa falsa.

Gabarito: A

É isso, pessoal! Espero que tenham curtido a resolução da prova de Geografia do vestibular UEL 2020. Sigam-me nas redes sociais. Têm muitas dicas lá. Mande uma mensagem, caso tenha tido alguma dúvida. Abraços!

Instagram: @professor.marcal

Gabarito UEL 2020 – Matemática – Resolução Comentada

UEL 2020

Questão 10

Resolução Comentada

Questão 30

Resolução Comentada

Questão 39

Resolução Comentada

Questão 40

Resolução Comentada

Questão 42

Resolução Comentada

Questão 47

Resolução Comentada

Questão 54

Resolução Comentada

Questão 58

Resolução Comentada

Raquel Oshio

Surrealismo: o que é, características e principais artistas

Gabarito UFPR 2020 – Física – Resolução Comentada

Círculo trigonométrico: o que é, exemplos, usos e aplicações

Aproximação sen(x) = tg(x) = x e suas aplicações no vestibular

Probabilidade no Enem: conceitos e como calcular

Gabarito UEL 2020 – Matemática – Resolução Comentada

UEL 2020

Questão 10

Resolução Comentada

Questão 30

Resolução Comentada

Questão 39

Resolução Comentada

Questão 40

Resolução Comentada

Questão 42

Resolução Comentada

Questão 47

Resolução Comentada

Questão 54

Resolução Comentada

Questão 58

Resolução Comentada

Raquel Oshio

Surrealismo: o que é, características e principais artistas

Gabarito UFPR 2020 – Física – Resolução Comentada

Você pode gostar também