Aproximação sen(x) = tg(x) = x e suas aplicações no vestibular

A aproximação $\dpi{100} \large sen\left(x\right)\approx tg(x)\approx x$ aparece em diversas questões e tópicos teóricos da física, principalmente. Vamos analisar onde essas aproximações aparecem, como devem ser utilizadas no vestibular e de onde ela surge (a demonstração da validade dessa aproximação envolve tópicos de cálculo diferencial, não sendo, portanto, necessária para o vestibular.

Navegue pelo conteúdo

De onde surge a aproximação?

Um dos tópicos do cálculo diferencial são as séries de Taylor, que são séries que utilizam as derivadas de uma função para representar uma função complicada em forma de um polinômio, que normalmente é muito mais fácil de ser estudado.

Não será mostrado aqui, mas a série de Taylor da função $\dpi{100} \large f(x) = sen (x)$ próxima ao ponto $\dpi{100} \large x = 0$ é dada por:

$\dpi{100} \large sen(x) = x - \frac{x^{3}}{3!}+\frac{x^{5}}{5!}-\frac{x^{7}}{7!}+\cdots =\textstyle\sum_{n=0}^{\infty} \frac{(-1)^{n}}{(2n+1)!}x^{2n+1}$

Sendo assim, perceba que, se tomarmos valores de x (em radianos) pequenos, o valor dos números $\dpi{100} \large \frac{x^{3}}{3!}$ , $\dpi{100} \large \frac{x^{5}}{5!}$ , e os demais se tornam muito pequenos se comparados com o valor de x.

Assim, torna-se válido e útil fazer a aproximação $\dpi{100} \large sen(x)\approx x$ . São considerados pequenos os valores de x até 10º (aproximadamente 0,17 radianos).

Note também que, para esse mesmo intervalo de valores de x (até 10º), $\dpi{100} \large cos(x)\approx 1$ . Como $\dpi{100} \large tg(x)=\frac{sen(x)}{cos(x)}$ , se $\dpi{100} \large cos(x)\approx 1$ , então $\dpi{100} \large tg(x)\approx sen(x)$ .

Outra análise

Outra forma um pouco mais visual de se perceber a validade dessa aproximação é analisando o ciclo trigonométrico.

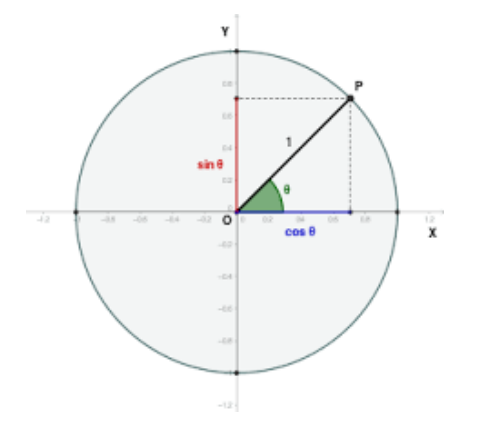
Analisando os elementos do ciclo, podemos perceber que, quanto menor o ângulo θ:

mais o valor de cosθ se aproxima da borda do círculo, ou seja, fica próximo de 1.
mais o valor de senθ, que é dado pela reta vertical, se aproxima do arco. Em outras palavras, quanto menor o ângulo, mais o trecho circular que corresponde ao arco se aproxima de uma reta, e para ângulos suficientemente pequenos, podemos tomar dessa reta como aproximação.

Ambas as observações nos levam a concluir mais uma vez que a aproximação é válida.

Como cai no vestibular?

Questão ITA 2015

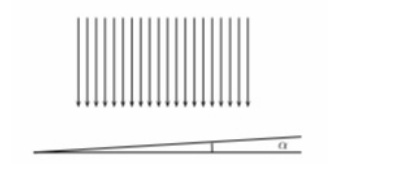
Luz, que pode ser decomposta em componentes de comprimento de onda com 480nm e 600 nm, incide verticalmente em uma cunha de vidro com ângulo de abertura $\dpi{100} \large \alpha = 3,00^{o}$ e incide de refração de 1,50, conforme a figura, formando linhas de interferência destrutivas. Qual é a distância entre essas linhas?

Resolução Comentada

O aparecimento das linhas de interferência destrutiva é causado pela espessura da cunha de vidro, que causa uma diferença de caminho entre a luz que é imediatamente refletida, percorre a cunha e então é refletida.

A diferença de caminhos nessa situação é dada por $\Delta d=2e$ , em que e é a espessura da cunha no ponto analisado.

Na reflexão do ar para a cunha ocorre inversão de fase, pois a cunha é mais refringente. Assim, os pontos em que ocorre interferência destrutiva são aqueles em que $\Delta d=2e=N\frac{\lambda }{n_{r}}(N=1,2,3...)$ sendo $n_{r}$ o índice de refração da cunha e $\lambda$ o comprimento de onda.

Só serão pontos de interferência destrutiva aqueles em que essa interferência acontecer para ambos os comprimentos de onda, ou seja, $\Delta d= N_{1}\lambda _{1}$ e $\Delta d= N_{2}\lambda _{2}$ .

Como o $\Delta d$ é o mesmo, podemos igualar as duas equações:

$N_{1}\lambda _{1} = N_{2}\lambda _{2}\rightarrow 480N_{1} = 600N_{2} \rightarrow 4N_{1} = 5N_{2}$ .

Os menores pares de números que satisfazem essa equação são $(N_{1}, N_{2}) = (5,4)$ e $(N_{1},N_{2}) = (10,8)$ . Com isso, conseguimos achar a espessura da cunha nos pontos desejados. No primeiro ponto, $\Delta =2e = \frac{5*480}{1,5}\rightarrow e=800 nm$ , e no segundo ponto $\Delta =2e = \frac{10*480}{1,5}\rightarrow e=1600 nm$ .

Agora, precisamos usar a aproximação. Queremos a distância horizontal entre esses dois pontos, e temos a distância vertical, dada por . Para isso, precisamos da tangente do ângulo de 3º é um ângulo pequeno, o que torna válida a aproximação $tg(\theta )\approx \theta$ , para $\theta$ em radianos.

Convertendo o ângulo para radianos, teremos que $3^{o}=\frac{3\pi }{180}=\frac{\pi }{60}\approx tg(3^{o})$ . Então, $x = \frac{800}{\frac{\pi }{60}}\approx 16 \cdot 10^{-6} = 16\mu m$ .

Geralmente, essa aproximação é usada apenas para um dos passos da solução de uma questão mais complicada, como é o caso da questão acima.

Aproximação sen(x) = tg(x) = x e suas aplicações no vestibular