Neste artigo, o Estratégia Vestibulares vai te ajudar a aprender o que é Função de Segundo Grau e como aplicá-la. A análise das funções de segundo grau seguirá o mesmo padrão que usamos para analisar as funções de primeiro grau.
A diferença é que nas funções de segundo grau teremos três coeficientes, não dois.
Pois bem. Uma função de segundo grau é da forma:
Alternativamente, podemos escrever
Sem perda de significado.
Como você deve ter notado, são três coeficientes; ?, ?, ?.
Uma particularidade da função de segundo grau é que o expoente dois torna valores negativos em positivos. É claro que isso não acontece com o termo de primeiro grau, mas, é um fator a se considerar quando estamos estudando gráficos de equações de segundo grau.
Como parâmetro, usaremos agora a função
Como todos os valores de ? serão elevados ao quadrado, essa função acaba sendo não negativa. Vejamos seu gráfico:
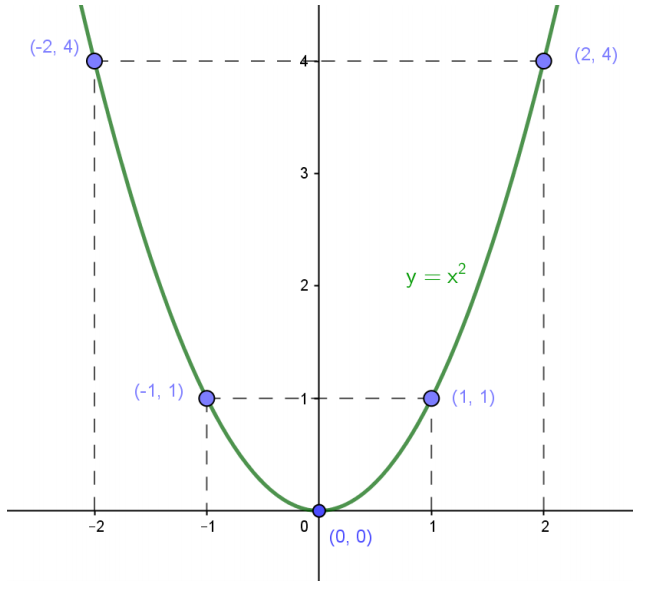
A função apresenta simetria axial (uma figura que tem, pelo menos, um eixo que a divide em duas partes semelhantes, iguais, correspondentes) e esse eixo é exatamente o eixo vertical, ou seja,
os valores de .
Essa característica é consequência do expoente par da função e a classifica como função par, mas veremos essa classificação na aula 02.
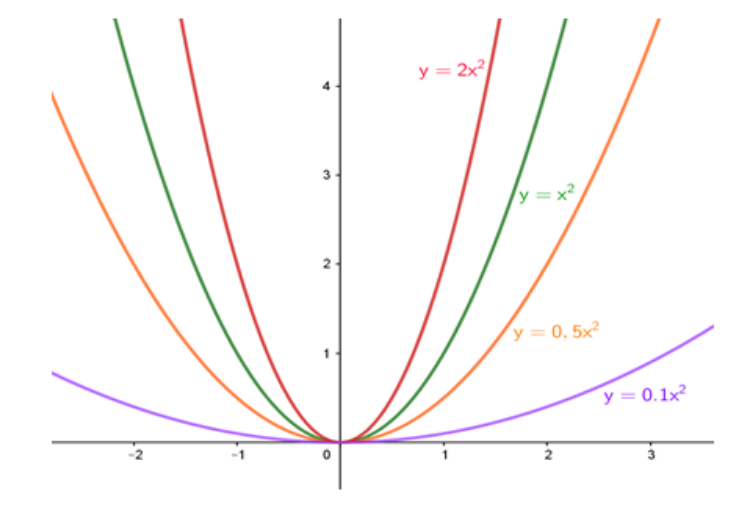
Por enquanto, basta notar a simetria e saber que nem toda função quadrática é par. Para a primeira análise, veremos como é afetada a função ao variarmos o coeficiente ?.
E qual seria a consequência de valores negativos no coeficiente ?? Seria esse valor negativo afetado pela potência de ??
Escrevendo a função com ? < 0, temos algo como em .
Nem o coeficiente ? nem o seu sinal estão elevados ao quadrado. Assim, o sinal de ? pode e deve ter interferência no gráfico da função. Só para deixar claro, aqui temos ? = −1.
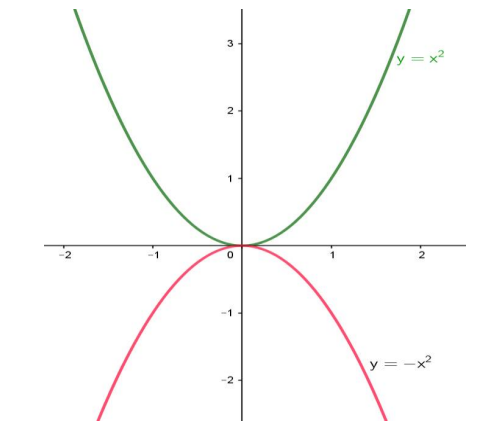
Nota-se que o coeficiente ? tem influência na abertura da função . A essa abertura, chamamos concavidade. Se o módulo de ? aumenta, a concavidade se fecha; se diminui, a concavidade se abre.
Além disso, valores negativos de ? resultam em funções com concavidades voltadas para baixo e positivos, para cima.
Essa curva que você notou nos gráficos recebe o nome de parábola e tem muitas características interessantes. Estudaremos essas propriedades com profundidade em Geometria Analítica e veremos, por exemplo, o motivo de usarmos antenas parabólicas para captar sinais de satélite.
Por enquanto o que nos interessa é o comportamento da função de segundo grau, cujo gráfico é representado por uma parábola.
Entendido o coeficiente ?, vamos para o coeficiente ?. Usemos a função
como base de comparação e alteremos o valor de ? = 0 para 1, 2 e 3.
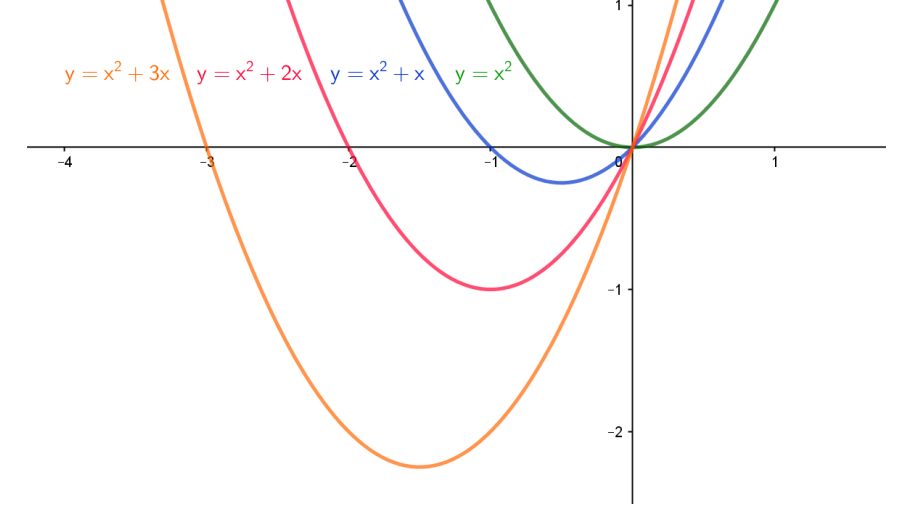
As parábolas se mantiveram “presas” na origem (0; 0), mas apareceu uma segunda raiz de módulo igual ao módulo de ?, mas com sinal contrário.
Vejamos o porquê de isso ocorrer.
Se temos uma função incompleta do tipo.
e queremos calcular suas raízes, nós colocaremos o valor zero no lugar da função, pois as raízes estão no eixo horizontal, lembra?
Se um produto é zero, um dos fatores deve ser igual a zero, então:
Como no nosso exemplo, ? = 1
Exatamente o comportamento visto:
parábola presa na origem
raiz com módulo igual ao módulo de b com sinal contrário.
Assim, apesar de não ser uma translação somente horizontal, ocorre um “escorregamento da função quanto alteramos o coeficiente ?.
Para confirmar, se o “escorregamento” sempre tem o sinal oposto de ?, se colocarmos valores negativos para o coeficiente ? a função “escorregaria” para a direita?
Teoricamente, sim. Façamos mais alguns gráficos só para confirmar.
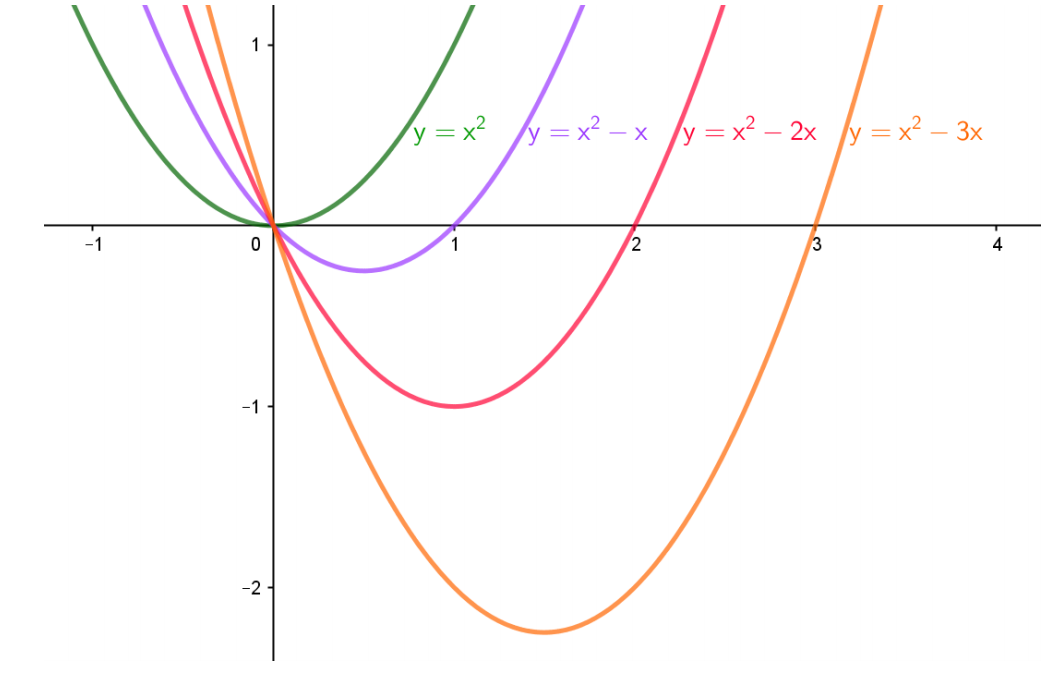
Exatamente o que esperávamos.
E, para encerrar esse estudo, analisemos o comportamento da função
quando variamos os valores do coeficiente ?.
Novamente, utilizaremos a função
como parâmetro e variaremos o coeficiente ? de 0 para −1,1, 2, 3.
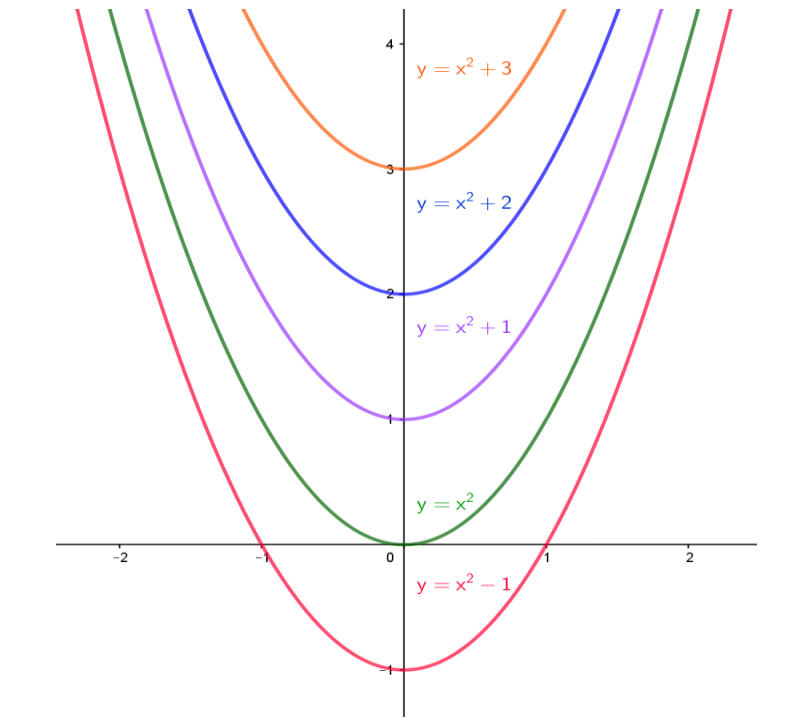
Não é de se estranhar que o termo independente da função de segundo grau também traz a informação do intercepto-y. Afinal, se colocarmos valor nulo na variável x, o que sobra é só o termo independente. Veja.
Ou seja, o termo independente traz exatamente o valor do ponto em que a função quadrática corta o eixo vertical.
Voltando às funções do gráfico, atenção à função
Ela apresenta duas raízes. Visualmente, no gráfico, vemos que devem ser {−1; 1}. Vamos conferir?
Para calcular as raízes, fazemos ? = 0, então:
Exatamente como prevíamos.
Agora, vejamos o que acontece com as funções que parecem “flutuar” no gráfico, não interceptando o eixo horizontal.
Vejamos o exemplo de
Perceba que não existe, no conjunto dos números reais, a raiz quadrada de número negativo.
Veja bem, tínhamos uma função e queríamos descobrir a(s) raiz(raízes). Par isso, substituímos ? por 0 e, nesse momento, passamos a ter uma equação que representa uma pergunta: qual o número cujo quadrado somado a um dá zero?
Quando chegamos a uma resposta inexistente, significa responder a essa pergunta dizendo: não existe número que satisfaça essa condição.
Como esse número representaria o(s) ponto(s) em que a função interceptaria o eixo horizontal, concluímos que a função está toda acima do eixo ou toda abaixo do eixo; não há intersecções entre esta e o eixo horizontal.
É extremamente importante que você esteja ciente do que calcula e, tanto quanto operar corretamente funções e equações, que consiga entender o que significam a cada momento.
Assim você poderá aplicar as ferramentas matemáticas para resolver problemas de forma eficiente. Isso ajuda a passar no vestibular e a resolver problemas do cotidiano por meio da matemática também.
Afinal, após o vestibular há toda uma faculdade a cursar, não é?
Navegue pelo conteúdo
Função de Segundo Grau – avançado
Vimos que as soluções para a equação
Ou, em sua forma alternativa,
Vimos também que para calcular as raízes de uma função, substituímos ? por zero.
Assim, o cálculo dos valores que satisfazem essa equação são também, quando no ambiente das funções quadráticas, suas raízes.
Sabemos também que não são todas as funções que têm raízes, algumas são estritamente positivas e outras, estritamente negativas; são os gráficos “flutuantes”.
Olhando para a forma alternativa de escrita para o cálculo das soluções da equação, percebesse que há uma raiz quadrada envolvida, a raiz quadrada do discriminante
Como não existe raiz de números negativos no conjunto dos números reais, temos que, para haver raízes em uma função, necessariamente
São duas possibilidades condensadas na informação: o discriminante pode ser zero ou o discriminante pode ser positivo.
Com o discriminante positivo, já vimos que há duas raízes distintas, portanto, a função corta o eixo horizontal duas vezes.
Caso o discriminante seja zero, vejamos o que acontece:
As duas raízes, ?′ e ?′′ passam a ser idênticas!
Dizemos que a função só tem uma raiz ou, mais tecnicamente, que tem apenas uma raiz de multiplicidade dois, pois funções do segundo grau devem ter duas raízes.
Nesse caso, a função apenas toca o eixo horizontal do gráfico, como vimos no caso de
Obviamente, caso a função apresente
ela não apresenta raízes reais, é estritamente positiva ou estritamente negativa e não toca o eixo das abcissas.
Mas professor, você não falou que toda função do segundo grau deve ter duas raízes, por isso a raiz única quando é chamada de raiz de multiplicidade dois?
Falei
Então, onde estão as duas raízes das funções que apresentam ?
Para o caso , existem também duas raízes, mas elas são do domínio dos números complexos. Perceba que eu disse que não havia raízes no conjunto dos números reais. Você aprenderá a calcular essas raízes na aula sobre números complexos, não se preocupe com isso agora.
Máximos e mínimos da função do segundo grau
A essa altura, você já deve ter percebido que as funções do segundo grau apresentam um ponto mais alto ou um ponto mais baixo, a depender do sinal do coeficiente ?.
Esse ponto é especial e, por ser um máximo ou um mínimo, interessa a muitos campos de estudo.
Por isso, é interessante acharmos um modo prático de encontrá-lo.
Vejamos um gráfico genérico de ?(?) = ??2 + ?? + c.
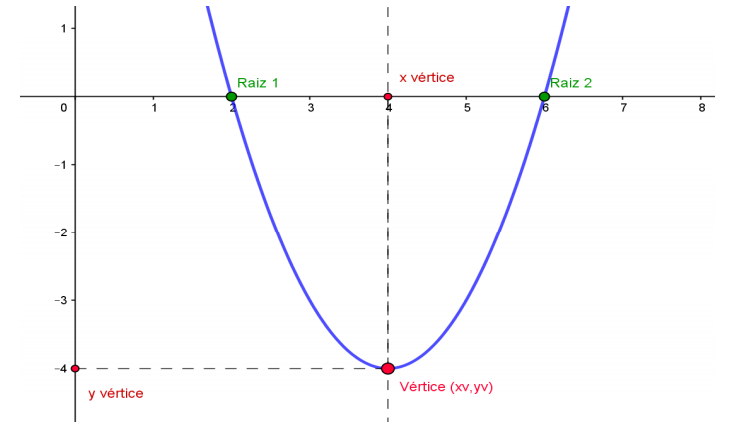
Ao ponto mais alto ou mais baixo da parábola, chamamos vértice e este tem duas coordenadas: x vértice e y vértice.
Como a parábola é simétrica, podemos dizer que a coordenada x do vértice, ou x vértice, está bem no meio entre as raízes, assim, podemos calculá-lo.
Se as raízes são dadas por:
Assim, podemos sempre saber qual a coordenada x do vértice pela fórmula acima. Perceba que descobrimos essa fórmula para o x-vértice () ao fazer a média entre as raízes, então, você também pode fazer isso se as conhecer:
Já para descobrir a coordenada y do vértice, podemos aplicar o valor de x vértice na própria função, veja:
Se aplicarmos a coordenada x do vértice, a coordenada y corresponderá, também, ao vértice.
Agora, sempre que precisarmos de máximos e mínimos de uma parábola, lembremos de seu vértice V:
Função de Segundo Grau em prova
Considerando a função
O valor de m para que f(x) tenha apenas uma raiz de multiplicidade dois é
a)
b)
c)
d)
e)
Resolvendo
Para que a função
tenha apenas uma raiz, é necessário que
Gabarito: E
Veja também:
- Função de Primeiro Grau: o que é e como aplicar em prova?
- Equação do primeiro grau: o que é, tipos, como resolver e questões
- Plano cartesiano: o que é, como se calcula e como cai em prova
- O que diz o teorema fundamental da álgebra?
- Teorema Fundamental da Aritmética: o que diz o teorema?
- Regra de sinais: o que é e como funciona o jogo de sinais
- Prova de matemática Fuvest 2020 com Resolução Comentada
- Resolução da prova de Matemática da 2ª Fase da Unicamp 2020
- Prova de Matemática UNESP 2020 com Resolução Comentada