Você certamente já se deparou com esse conteúdo. Afinal, é assunto básico que todo estudante precisa ter alguma noção para não ser pego de surpresa no vestibular. Função de primeiro grau é a função do tipo ? = ?? + ?.
Algumas características das funções de primeiro grau merecem destaque quando falamos sobre equações do primeiro grau, vamos a elas.
Navegue pelo conteúdo
Características da Função de Primeiro Grau
Há, na escrita da função, os coeficientes ? e ?. Atenção, eles não são variáveis, mas coeficientes.
E qual será o papel deles quando esboçamos o gráfico de equações de primeiro grau? O que faremos aqui não é uma “prova” matemática.
Os gráficos que serão apresentados têm a função de explicitar comportamentos conhecidos das funções de primeiro grau a título de apresentação.
Em pontos diferentes do curso veremos algumas provas do que será introduzido intuitivamente nos próximos passos. Feitas as considerações, façamos alguns gráficos para análise.
Para padronizar, levaremos em consideração a seguinte função de primeiro grau
Também conhecida por função afim.
Vejamos seu gráfico.
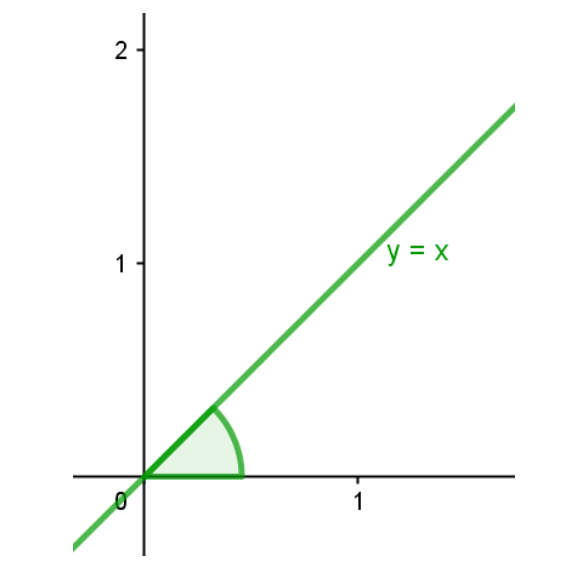
Alterando os valores do coeficiente de 1 para 2, 3 ? 4.
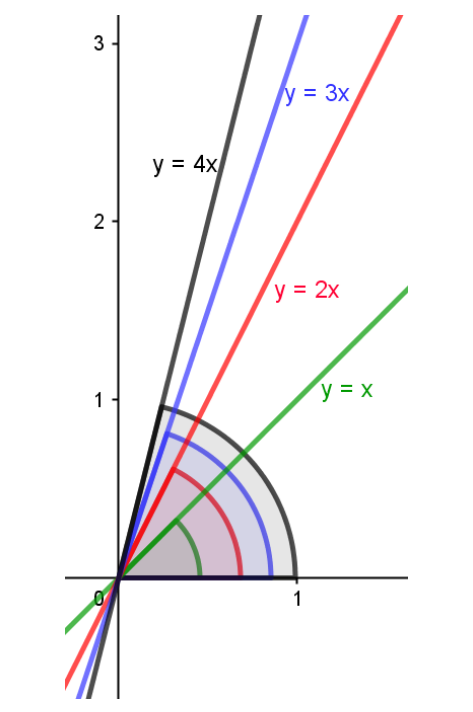
Você deve ter notado que, aparentemente, todas as funções de primeiro grau parecem ser retas. Conversaremos sobre isso mais à frente.
Sobre o coeficiente ?, percebeu que quando o aumentamos, também aumenta o ângulo entre a reta ? e o eixo ??
Além disso, todas se interceptam no ponto (?; ?) = (0; 0), o que era de se esperar. Como as funções são todas do tipo
? = ??
quando
? = 0 → ? = ?. 0 = 0.
E o que será que acontece quando colocamos um número negativo no lugar do coeficiente ??
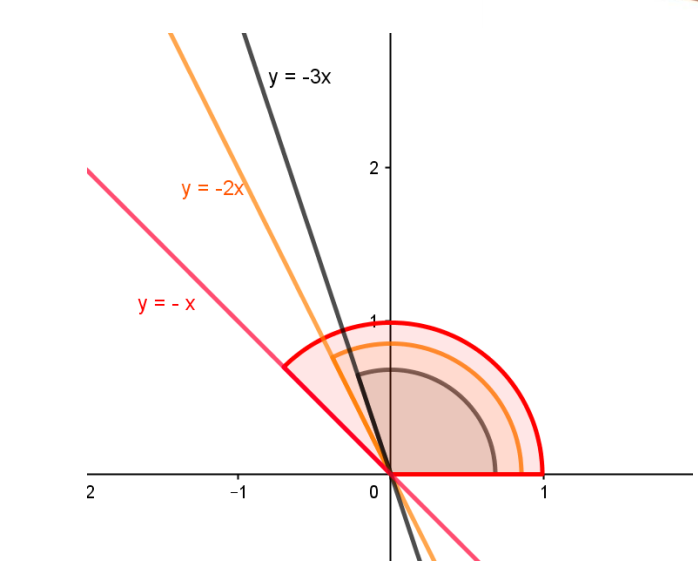
Todas as retas apresentam ângulo maior que 90° com o eixo ?.
Podemos perceber alguns comportamentos da função de primeiro grau referentes ao coeficiente ?:
- Quanto maior o valor do módulo de ?, mais vertical a reta.
- Coeficientes positivos geram retas crescentes.
- Coeficientes negativos geram retas decrescentes.
- Todas as retas da forma ? = ?? cruzam a origem do plano cartesiano (0; 0).
Está evidente a importância do coeficiente ? para o ângulo entre a reta ? = ?? e o eixo ?. Essa característica levou à designação do coeficiente ? como coeficiente angular.
Entendido o papel do coeficiente angular ? para a função de primeiro grau, passemos ao estudo do coeficiente ?.
Para padronização, utilizaremos a mesma função: ? = 1? + 0 ⇒ ? = ?.
Como fizemos com o coeficiente angular, alteremos o valor do coeficiente ? de 0 para 1, 2 ? 3.
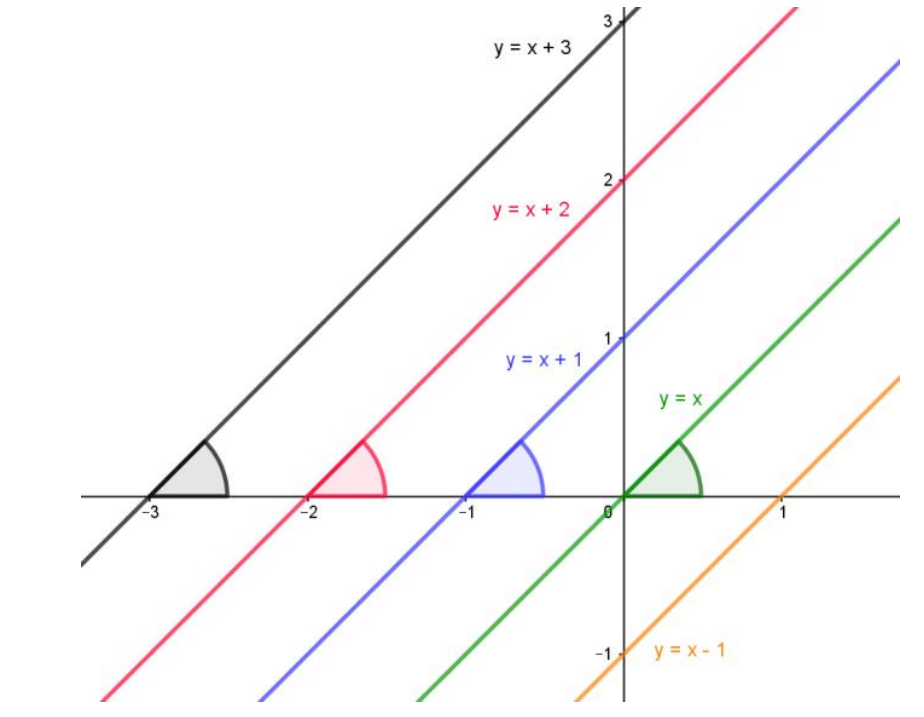
Que figura curiosa.
Note que todas as retas apresentam o mesmo ângulo com o eixo ?, das abcissas. Afinal, se o coeficiente angular de todas essas retas é o mesmo, ? = 1, não poderíamos esperar diferente, não é mesmo?
Já a mudança do coeficiente ? causou um deslocamento do ponto de intersecção da reta com o eixo ?. Antes, todas as retas tocavam o eixo das ordenadas na origem. Ao alterar o coeficiente ?, o ponto de intersecção não só foi alterado, como apresenta o mesmo valor numérico do coeficiente.
Vejamos essa característica algebricamente.
O ponto onde a reta corta o eixo ? tem sempre coordenada (0; ?). Sendo assim, funções do tipo
? = ?? + ?
ao interceptarem o eixo das ordenadas, sempre em um ponto (0; ?), ou seja, ? = 0, apresentará valor calculado no ponto por:
? = 0? + ?
Essa relação entre o ponto de intersecção entre a reta e o eixo ?, também chamado de intercepto-y, dá origem ao nome ao coeficiente ? de coeficiente linear; o valor onde a reta “corta” a linha do eixo vertical.
Com esses dados acerca dos coeficientes angular e linear, já somos capazes de esboçar o gráfico das funções de primeiro grau apenas olhando para ? e ?.
Testemos nossas habilidades. Como seria o gráfico de, digamos, ? = −2? + 5?
O gráfico dessa função de primeiro grau deve ser decrescente, pois o coeficiente linear ? é negativo; e interceptar o eixo ? em (0; 5), pois o coeficiente linear é ? = 5.
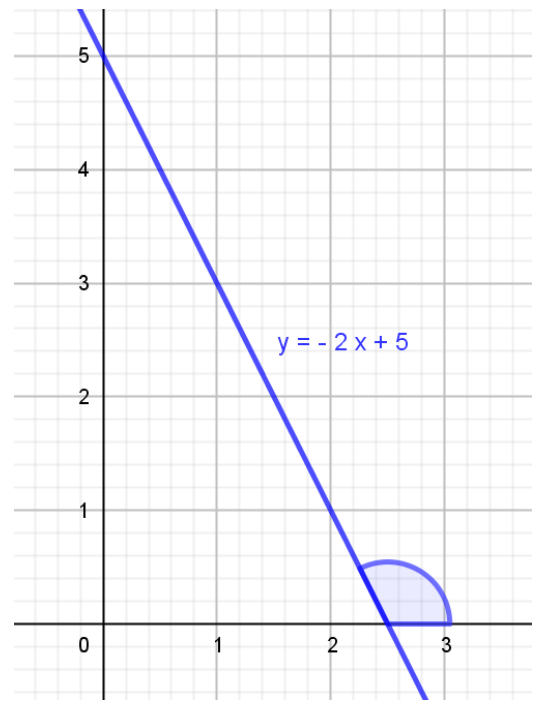
Professor, nós falamos do intercepto-y, mas e o ponto em que a função corta o eixo ??
Excelente pergunta!
Esse ponto se chama intercepto-x, zero da função ou ainda, raiz da função.
Se os pontos do eixo vertical todos têm coordenadas ? = 0, algo parecido acontece com o eixo horizontal: todos os pontos têm coordenadas ? = 0.
Para saber onde a função corta o eixo ?, basta substituir ? = 0 na função. E isso funciona para todas as funções, não só para as funções de primeiro grau.
No gráfico, percebemos que a raiz é algo entre 2 e 3, mas não temos precisão para defini-la apenas graficamente.
Vamos calculá-la.
Assim, dizemos que a raiz da função
é
Professor, se o coeficiente ? for nulo, a reta passa pela origem, correto?
Correto.
E o coeficiente ?, pode ser nulo também?
Pergunta interessante, vejamos o que acontece se substituirmos o coeficiente angular ? por 0.
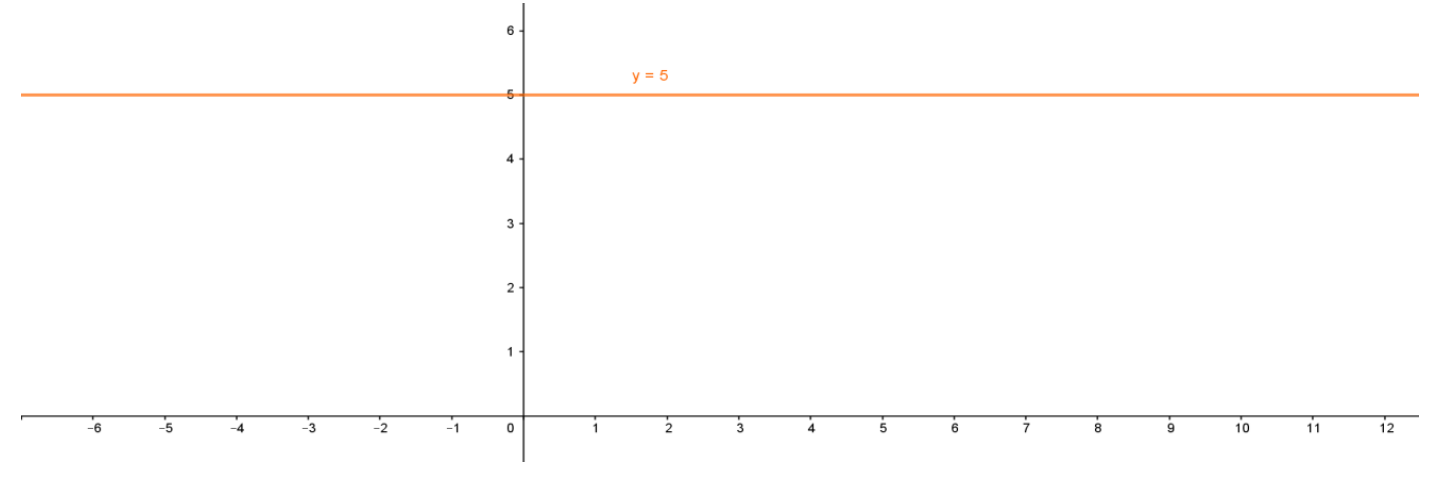
Como padrão de comparação, usaremos a função cujo gráfico acabamos de esboçar ? = −2? + 5 .
Substituindo o coeficiente angular por 0, temos
? = 0. ? + 5
? = 5
Isso significa que não há onde substituirmos o valor de ?, ou seja, para qualquer valor de ?, ? = 5 e não há variação. Esse tipo de função é chamado de função constante e, para esse caso específico, tem o seguinte gráfico:
Você notou como passamos de uma função para uma equação quando foi preciso calcular a raiz? É muito importante que você esteja ciente dos passos enquanto aprende e enquanto resolve os exercícios. Lembre-se de praticar com simulados para manter-se afiado, combinado?
Resumindo
De acordo com o que vimos até agora, há 6 tipos principais de funções de primeiro grau, ?(?) = ?? + ?, não constantes, veja a seguir:
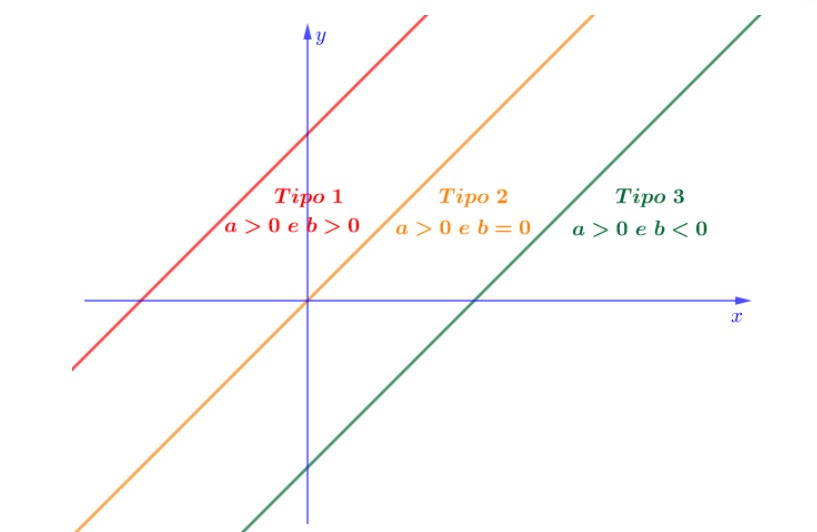
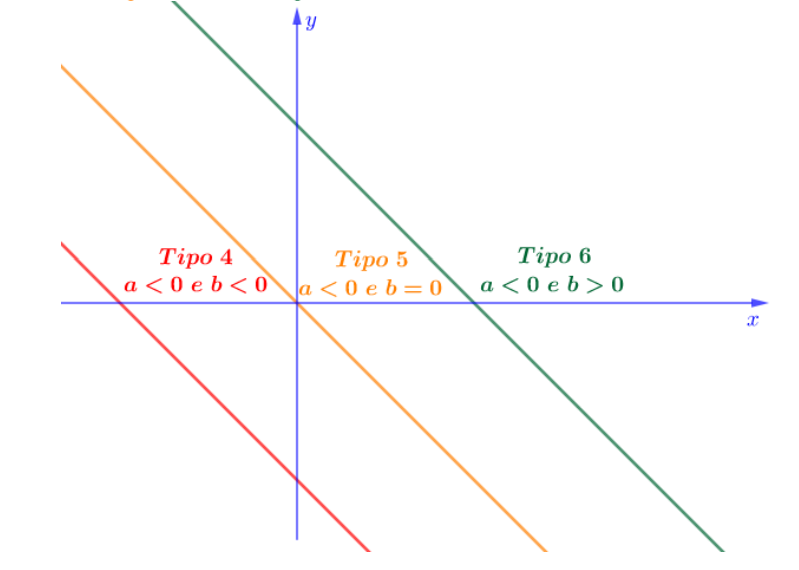
Atenção, apenas nomeamos os tipos de função de 1 a 6 para numerar os tipos com um fim didático. Não se refira em uma prova a uma função do tipo 5, por exemplo. Em vez disso, explicite as condições dos coeficientes ? e ?.
Exercício de Fixação
Função de Primeiro Grau
Esboce o gráfico de cada uma das funções abaixo.
a)
b)
c)
d)
e)
f)
g)
h)
i)
j)
Respostas:
a) ? > 0, ? > 0,???? 1
b) ? < 0, ? = 0,???? 5
c) ? > 0, ? > 0,???? 1
d) ? > 0, ? < 0,???? 3
e) ? < 0, ? > 0,???? 6
f) ? > 0, ? < 0,???? 3
d) ? > 0, ? > 0,???? 1
h) ? > 0, ? = 0,???? 2
i) ? < 0, ? > 0,???? 6
j) ? < 0, ? < 0,???? 4
Veja também:
- Equação do primeiro grau: o que é, tipos, como resolver e questões
- Função de Segundo Grau: o que é e como resolver questões
- Plano cartesiano: o que é, como se calcula e como cai em prova
- O que diz o teorema fundamental da álgebra?
- Teorema Fundamental da Aritmética: o que diz o teorema?
- Regra de sinais: o que é e como funciona o jogo de sinais
- Prova de matemática Fuvest 2020 com Resolução Comentada
- Resolução da prova de Matemática da 2ª Fase da Unicamp 2020
- Prova de Matemática UNESP 2020 com Resolução Comentada




