Prova de Matemática UNESP 2020 com Resolução Comentada

Olá, pessoal… Tudo bem? Sou a prof. Marçal, do Estratégia Vestibulares, e escrevo este artigo para lançar o Gabarito UNESP 2020, da disciplina de Matemática. Nesta página, você vai conferir a resolução comentada completa. Vamos nessa??

">Prova UNESP 2020 – Matemática – Correção" class="wp-block-file__button" download>Baixar

Navegue pelo conteúdo

Prova UNESP 2020

Questão 84

De acordo com levantamento realizado de janeiro a outubro de 2018, o Brasil apareceu em primeiro lugar como o país em que cada habitante mais recebeu chamadas telefônicas spam, que incluem ligações indesejadas de telemarketing, trotes e golpes. A tabela mostra o número médio de chamadas spam recebidas mensalmente por usuário no Brasil e em outros países.

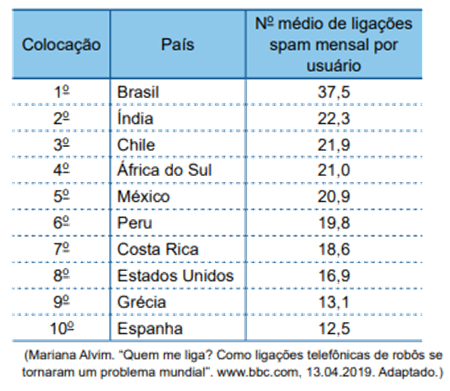
A diferença entre o número médio de chamadas spam recebidas mensalmente por usuário no Brasil e a média aritmética do número médio de chamadas spam recebidas mensalmente por usuário nos demais países da América Latina apresentados na tabela é igual a

(A) 17,2.
(B) 17,4.
(C) 16,7.
(D) 16,6.
(E) 17,9.

Resolução Comentada

Perceba que precisamos de dois dados para calcular a diferença solicitada:

Número de spams no Brasil

Média dos spams nos países da América Latina

O perigo aqui é listar os países da América latina incorretamente, então, cuidado.

Vamos, então, colher os dados de que precisamos.

Média do Brasil: 37,5

Valores dos países da América Latina:

Chile: 21,9
México: 20,9
Peru: 19,8
Costa Rica: 18,6
Total: 81,2

Média dos países da América Latina:

$\dpi{100} \large \frac{81,2}{4}=20,3$

Diferença:

$\dpi{100} \large 37,5-20,3=17,2$

Gabarito: A

Questão 86

Uma cidade tem sua área territorial dividida em quatro regiões. O esquema apresenta, de modo simplificado, a área territorial e a densidade populacional dessas quatro regiões:

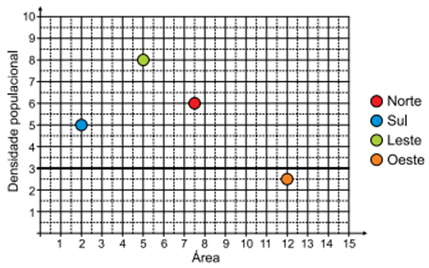
A participação das populações dessas regiões na população total da cidade é:

Como o enunciado não explicitou as unidades, vamos nomeá-las genericamente. Chamemos a unidade da área de $\dpi{100} \large ua$ e a densidade populacional de $\dpi{100} \large \frac{H}{ua}$ , onde $\dpi{100} \large H$ representa a quantidade de habitantes. Dessa forma, um produto das coordenadas de cada ponto nos dará a quantidade de habitantes $\dpi{100} \large H$ , veja:

Note:

$\dpi{100} \large 7,5ua\cdot 6\frac{H}{ua}=45H$

Sul:

$\dpi{100} \large 2ua\cdot 5\frac{H}{ua}=10H$

Leste:

$\dpi{100} \large 5ua\cdot 8\frac{H}{ua}=40H$

Oeste:

$\dpi{100} \large 12ua\cdot 2,5\frac{H}{ua}=30H$

Com esses dados, podemos calcular o total de habitantes na soma das regiões:

$\dpi{100} \large 45H+10H+40H+30H$

$\dpi{100} \large 125H$

Dessa forma, podemos calcular qual a razão entre o número de habitantes em uma dada região e o total.

Norte:

$\dpi{100} \large \frac{45}{125}=\frac{9}{25}$

Sul:

$\dpi{100} \large \frac{10}{125}=\frac{2}{25}$

Leste:

$\dpi{100} \large \frac{40}{125}=\frac{8}{25}$

Oeste:

$\dpi{100} \large \frac{30}{125}=\frac{6}{25}$

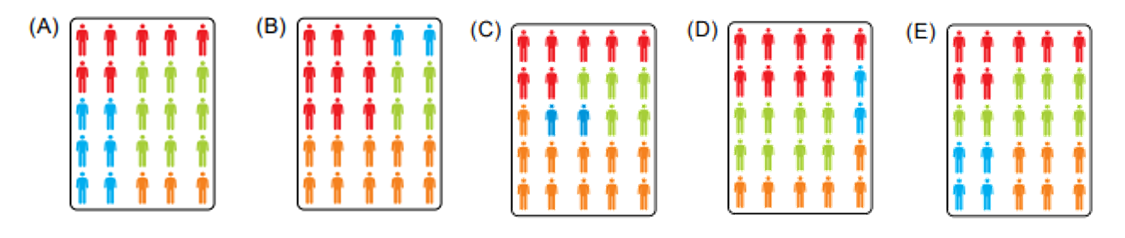
Essas frações são muito propícias, visto que temos que compará-las à quantidade presente de cada região em um esquema apresentado nas alternativas que contém, coincidentemente, a população representada por uma divisão de 25 partes, uma para cada pessoa do diagrama.

Assim, a única representação que apresenta 9 partes para a região norte, 2 partes para a região sul, 8 partes para a região leste e 6 para a região oeste está na alternativa d).

Gabarito: D

Questão 87

O quilate do ouro é a razão entre a massa de ouro presente e a massa total da peça, multiplicada por 24. Por exemplo, uma amostra com 18 partes em massa de ouro e 6 partes em massa de outro metal (ou liga metálica) é um ouro de 18 quilates. Assim, um objeto de ouro de 18 quilates tem de ouro e de outro metal em massa.

O ouro é utilizado na confecção de muitos objetos, inclusive em premiações esportivas. A taça da copa do mundo de futebol masculino é um exemplo desses objetos.

A FIFA declara que a taça da copa do mundo de futebol masculino é maciça (sem nenhuma parte oca) e sua massa é de pouco mais de 6 kg. Acontece que, se a taça fosse mesmo de ouro e maciça, ela pesaria mais do que o informado. (“O peso da taça”. https://ipemsp.wordpress.com. Adaptado.)

Considere que a taça seja feita apenas com ouro 18 quilates, cuja composição é de ouro com densidade 19,3 g/cm³ e uma liga metálica com densidade 6,1 g/cm³ , e que o volume da taça é similar ao de um cilindro reto com 5 cm de raio e 36 cm de altura.

Utilizando π = 3, se a taça fosse maciça, sua massa teria um valor entre

(A) 30 kg e 35 kg.

(B) 15 kg e 20 kg.

(D) 10 kg e 15 kg.

(E) 20 kg e 25 kg.

Resolução Comentada

Como temos que comparar o volume com o volume de um cilindro, vamos, de início, já calculá-lo.

Volume do cilindro

$\dpi{100} \large V=\pi \cdotr^{2}\cdot h$

$\dpi{100} \large V=3\cdot5^2\cdot36$

$\dpi{100} \large V=2700\ cm^3$

Agora, precisamos montar um sistema de equações em que $\dpi{100} \large \frac{3}{4}$ da massa seja ocupada pelo ouro e $\dpi{100} \large \frac{1}{4}$ da massa, pela liga metálica.

Como não sabemos qual o volume ocupado pela liga metálica, vamos nomeá-lo v.

Dessa forma, temos:

$\dpi{100} \large \left\{\begin{matrix}\frac{3}{4}m=\left(2700-v\right)\cdot19,3\\\ \\\frac{1}{4}m=v\cdot6,1\\\end{matrix}\right.\rightarrow\left\{\begin{matrix}3m=\left(2700-v\right)\cdot77,2\\\ \\m=v\cdot24,4\\\end{matrix}\right.\rightarrow\left\{\begin{matrix}3m=208440-77,2\cdot v\\\ \\m-v\cdot24,4=0\\\end{matrix}\right.$

$\dpi{100} \large \rightarrow\left\{\begin{matrix}3m+77,2\cdot v=208440\\\ \\m-v\cdot24,4=0\\\end{matrix}\right.\rightarrow\left\{\begin{matrix}m=33.816,06\ g\\\ \\v=1385,9\ cm^3\\\end{matrix}\right.\rightarrow\left\{\begin{matrix}m=33,81606\ kg\\\ \\v=1385,9\ cm^3\\\end{matrix}\right.$

Dessa forma, o valor da massa da taça seria de, aproximadamente, $\dpi{100} \large m=33,81606\ kg$ , portanto, gabarito a).

No entanto, a banca publicou de início outro gabarito.

A título de especulação, pode ter havido um erro no enunciado: considerar a razão entre os volumes sendo o mesmo que a razão entre as massas.

Apesar de incorreto, é um erro comum e levaria ao seguinte desfecho:

$\dpi{100} \large \frac{3}{4}\cdot2700\cdot19,3+\frac{1}{4}\cdot2700\cdot6,1$

$\dpi{100} \large 39.082,5+4.117,5$

$\dpi{100} \large 43.200\ g$

$\dpi{100} \large 43,2\ kg$

Resultando no gabarito c), considerado correto preliminarmente pela banca.

Consideramos como gabarito correto a alternativa a), portanto, deixando a questão passível de recurso para mudança de gabarito.

Gabarito Banca: C
Gabarito Estratégia: A

Questão 88

Uma das finalidades da Ciência Forense é auxiliar nas investigações relativas à justiça civil ou criminal. Observe uma ideia que pode ser empregada na análise de uma cena de crime. Uma gota de sangue que cai perfeitamente na vertical, formando um ângulo de 90º com a horizontal, deixa uma mancha redonda. À medida que o ângulo de impacto com a horizontal diminui, a mancha fica cada vez mais longa. As ilustrações mostram o alongamento da gota de sangue e a relação trigonométrica envolvendo o ângulo de impacto e suas dimensões.

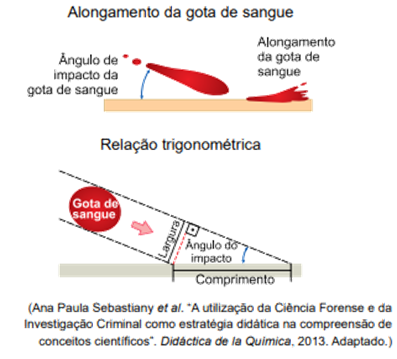
Considere a coleta de uma amostra de gota de sangue e a tabela trigonométrica apresentadas a seguir.

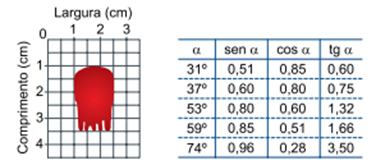
De acordo com as informações, o ângulo de impacto da gota de sangue coletada na amostra foi de

(A) 37°

(B) 74°

(D) 53°

(E) 31°

Resolução Comentada

Na linguagem do enunciado, vamos colher os valores da largura e do comprimento da gota, diretamente do diagrama fornecido.

Largura – $\dpi{100} \large 2,5-1=1,5$

Comprimento – $\dpi{100} \large 3,5-1=2,5$

De posse desses dados, podemos partir para a relação trigonométrica. Pela

$\dpi{100} \large sen\left(\alpha\right)=\frac{co}{hip}$

$\dpi{100} \large sen\left(\alpha\right)=\frac{largura}{comprimento}$

$\dpi{100} \large sen\left(\alpha\right)=\frac{1,5}{2,5}$

$\dpi{100} \large sen\left(\alpha\right)=\frac{6}{10}$

$\dpi{100} \large sen\left(\alpha\right)=0,6$

$\dpi{100} \large \alpha=37\degree$

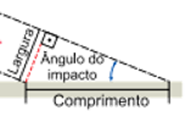
Gabarito: A

Questão 89

Em seu artigo “Sal, saúde e doença”, o médico cancerologista Dráuzio Varella aponta que o Ministério da Saúde recomenda que a ingestão diária de sal não ultrapasse 5 g, quantidade muito abaixo dos 12 g, que é a média que o brasileiro ingere todos os dias. Essa recomendação do Ministério da Saúde é a meta que a Organização Mundial da Saúde estabeleceu para até 2025. Além disso, o ministério estima que, para cada grama de sal reduzido na ingestão diária, o SUS economizaria R$ 3,2 milhões por ano. (Dados extraídos de: “Sal, saúde e doença”. https://drauziovarella.uol.com.br, 24.05.2019. Adaptado.)

Considere que a ingestão média diária de sal no Brasil reduza-se de 12 g, em 2019, para 5 g, em 2025, de forma linear, ano a ano. Nesse cenário, o SUS economizaria, até o final do ano de 2025, um valor entre

(A) R$ 65 milhões e R$ 70 milhões.

(B) R$ 75 milhões e R$ 80 milhões.

(D) R$ 20 milhões e R$ 25 milhões.

(E) R$ 55 milhões e R$ 60 milhões.

Resolução Comentada

Em 6 anos, haverá economia de $\dpi{100} \large 12-5=7\ gramas$ .

$\dpi{100} \large \frac{7\ gramas}{6\ anos}=\frac{7}{6}\ g/a$

Fazendo uma sequência do consumo em gramas por ano, temos:

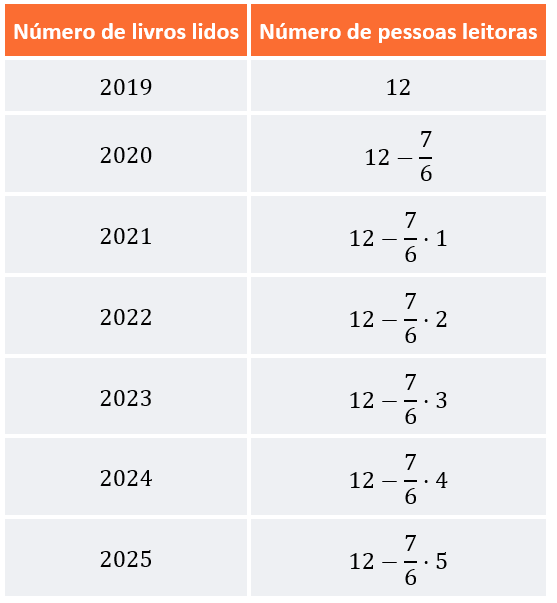
A economia total feita pode ser considerada como a soma das economias feitas a cada ano, ou seja:

$\dpi{100} \large Economia=\frac{7}{6}+\frac{7}{6}\cdot2+\frac{7}{6}\cdot3+\frac{7}{6}\cdot4+\frac{7}{6}\cdot5+\frac{7}{6}\cdot6$

Obviamente, você pode fazer a soma na mão. No entanto, para facilitar, podemos pensar como sendo a soma dos seis elementos de uma PA de razão $\dpi{100} \large \frac{7}{6}$ .

$\dpi{100} \large S_6=\frac{\left(a_1+a_6\right)\cdot6}{2}=\left(\frac{7}{6}+7\right)\cdot3=24,5$

Agora, para calcularmos a economia em milhões de reais, podemos fazer o produto da economia em gramas pelo fator de economia por grama economizada.

$\dpi{100} \large Valor\ economizado=24,5\cdot3,2=78,4\ Milhoes$

Gabarito: B

Questão 90

Considere os polinômios $\dpi{100} \large p\left(x\right)=\left|\begin{matrix}x&1&0\\2&x&-1\\m&x&x\\\end{matrix}\right|$ e $\dpi{100} \large q\left(x\right)=\left|\begin{matrix}1&3\\1&x\\\end{matrix}\right|$ . Para que p(x) seja divisível por ?(?), é necessário que m seja igual a:

(A) 30.

(B) 12.

(D) –3.

(E) –30.

Resolução Comentada

Para que o polinômio $\dpi{100} \large p\left(x\right)=\left|\begin{matrix}x&1&0\\2&x&-1\\m&x&x\\\end{matrix}\right|$ seja divisível por $\dpi{100} \large q\left(x\right)=\left|\begin{matrix}1&3\\1&x\\\end{matrix}\right|$ , precisamos calcular a raiz de ?(?).

$\dpi{100} \large q\left(x\right)=0$

$\dpi{100} \large \left|\begin{matrix}1&3\\1&x\\\end{matrix}\right|=0$

$\dpi{100} \large x-3=0$

$\dpi{100} \large x=3$

A condição necessária para que p(x) seja divisível por ?(?), pelo teorema do resto, é que $\dpi{100} \large p(3)=0$ .

$\dpi{100} \large p\left(3\right)=0$

$\dpi{100} \large \left|\begin{matrix}3&1&0\\2&3&-1\\m&3&3\\\end{matrix}\right|=0$

$\dpi{100} \large 3^3-m-6+9=0$

$\dpi{100} \large 27-6+9=m$

$\dpi{100} \large 30=m$

Gabarito: A

É isso, pessoal! Espero que tenham curtido a resolução da prova de Matemática do vestibular UNESP 2020. Sigam-me nas redes sociais. Têm muitas dicas lá. Mande uma mensagem, caso tenha tido alguma dúvida. Abraços!

Instagram: @professor.marcal

Prova de Matemática UNESP 2020 com Resolução Comentada

Prova UNESP 2020

Questão 84

Resolução Comentada

Questão 86

Questão 87

Resolução Comentada

Questão 88

Resolução Comentada

Questão 89

Resolução Comentada

Questão 90

Resolução Comentada

Veja também:

Raquel Oshio

Gabarito UNESP 2020 – Física – Prova Resolvida

Gabarito Unicamp 2020 – Biologia – Resolução Comentada

Função modular: o que é, propriedades, exercícios de vestibulares

Porcentagem: o que é, como calcular e mais

Funções: definição, características e tipos

Prova de Matemática UNESP 2020 com Resolução Comentada

Prova UNESP 2020

Questão 84

Resolução Comentada

Questão 86

Questão 87

Resolução Comentada

Questão 88

Resolução Comentada

Questão 89

Resolução Comentada

Questão 90

Resolução Comentada

Veja também:

Raquel Oshio

Gabarito UNESP 2020 – Física – Prova Resolvida

Gabarito Unicamp 2020 – Biologia – Resolução Comentada

Você pode gostar também