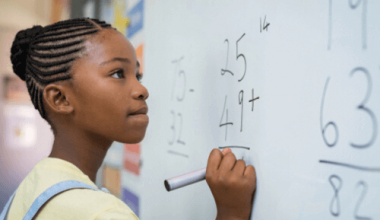A matemática está presente em diversos aspectos da nossa sociedade, além de ser muito importante na escola e recorrente no vestibular. Por isso, conhecer os assuntos básicos como a regra de três, as quatro operações, funções de primeiro e segundo grau, áreas de figuras planas, entre outras é essencial.
Por isso, o Estratégia Vestibulares preparou um artigo que reúne as dúvidas mais relevantes sobre a regra de três simples e composta. Acompanhe!
Navegue pelo conteúdo
O que é regra de três?
A regra de três é uma forma de cálculo para encontrar valores proporcionais entre grandezas que se relacionam entre si.
A regra de três pode associar números diretamente proporcionais ou inversamente proporcionais. Para compreender melhor esses conceitos, leia o tópico abaixo.
Grandezas direta e inversamente proporcionais
Grandezas diretamente proporcionais são aquelas que “crescem” e “decrescem” juntas.
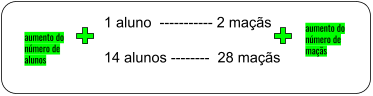
Por exemplo, imagine que é determinado que cada aluno da turma B come duas maçãs. Na sala de aula, temos catorze alunos. Portanto, serão necessárias 28 maçãs para alimentar a turma B.
Note como o aumento do número de alunos causou o aumento do número de maçãs necessárias – isso indica uma proporcionalidade direta entre as grandezas “aluno” e “maçã”.
Já as grandezas inversamente proporcionais se relacionam de maneira oposta. Ou seja, quando uma “cresce” a outra “decresce” e vice-versa.
Por exemplo, quanto maior a velocidade do seu carro, menor o tempo para chegar ao destino. Isto é, o aumento da velocidade causa a diminuição do tempo de viagem e o contrário é verdadeiro.
Como calcular regra de três simples?
A regra de três simples relaciona 3 valores conhecidos e um valor desconhecido.
Com o mesmo exemplo de alunos e frutas, imagine que cada aluno da turma B come 4 uvas. Para um passeio da turma, foram compradas 64 uvas. Quantos alunos foram ao passeio?
Para relacionar as grandezas, pode-se construir um esquema que coloque uvas em uma coluna e o número de alunos em outra coluna. Depois, você deve entender se existe uma proporcionalidade direta ou indireta entre os valores.
Quando o número de alunos aumenta, o número de uvas também aumenta. Ou seja, é uma relação diretamente proporcional.
A partir disso, você deve multiplicar em x os elementos da coluna:
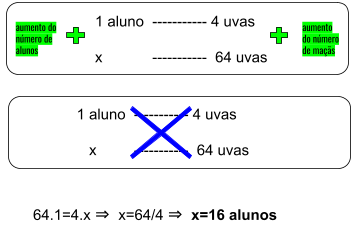
Perceba que após a montagem da tabela, a função descrita será uma equação de primeiro grau e permite encontrar o número de 16 alunos que foram ao passeio.
Se, após construir o esquema de regra de três, você notou uma proporção inversa entre as grandezas, é preciso inverter um dos lados da igualdade. Acompanhe um exemplo:
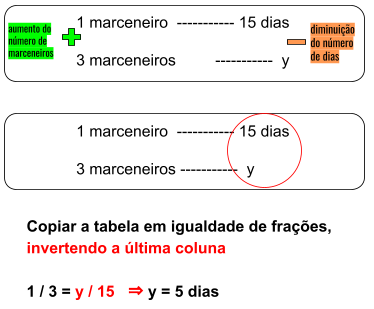
Se um marceneiro constrói um guarda-roupas em 15 dias. Três marceneiros, juntos, construirão esse guarda roupas em quantos dias?
Perceba que o aumento do número de profissionais diminuirá o tempo de construção, como uma inversão de igualdades.
Como calcular regra de três composta?
Agora que você já conhece a regra de três simples, aprenda sobre a parte composta do método.Nesse caso, aparecerão 5 valores e uma incógnita. Para encontrá-la, é importante determinar a proporção direta/indireta entre as grandezas.
Por exemplo, um marceneiro constrói um guarda-roupas em 15 dias, trabalhando 10 horas por dia. Cinco marceneiros trabalhando 5 horas por dia construirão esse guarda roupas em quantos dias?

Após determinar a proporcionalidade entre as grandes, é necessário escolher uma delas como norte. Escolhendo o número de dias como parâmetro, as horas e os marceneiros serão inversamente proporcionais. Baseado nisso, cria-se a equação, que mantém a fração do número de dias e igual às outras grandezas, com fração invertida. Veja na imagem:
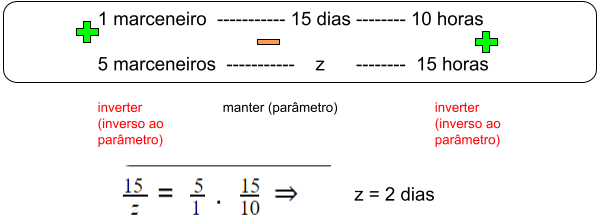
Atente-se ao fato de que a inversão ou mantimento das frações depende de qual grandeza você definiu como parâmetro. Ou seja, quando elas são inversamente proporcionais ocorre a inversão da fração, em que o contrário é verdadeiro.
Exercícios
ENEM 2017
Uma televisão pode ser posicionada de modo que se consiga enxergar os detalhes de uma imagem em alta definição. Considere que a distância ideal, com conforto visual, para se assistir à televisão de 32 polegadas é de 1,8 metro. Suponha que haja uma relação de proporcionalidade direta entre o tamanho da tela (medido em polegada) e a distância ideal. Considere que um espectador dispõe de uma televisão de 60 polegadas e que ele deseja se posicionar em frente a ela, com conforto visual.
A distância da televisão, em metro, em que o espectador deve se posicionar para que tenha conforto visual é mais próxima de
a) 0,33
b) 0,96
c) 1,57
d) 3,37
e) 3,60
Como o enunciado aponta uma proporcionalidade direta e trás 3 incógnitas, deve ser utilizada a regra de três simples e direta para encontrar o valor da incógnita:
32 polegadas —— 1,8 metros
60 polegadas —— x metros
x.32 = 1,8.60 ⇒ x.32 = 108 ⇒ x=108/32 ⇒ x=3,375
Nessa questão, os números aparecem com a terceira casa decimal suprimida, portanto, o número mais próximo do valor de x é a alternativa d.
Tem dificuldade com matemática? Acompanhe o Blog do Estratégia e tenha acesso às principais informações e dicas sobre álgebra.
Para conhecer nossos cursos pré-vestibulares, clique no banner abaixo:
Veja também:
- Moda, média, mediana: o que é e como cai no vestibular?
- Matemática para Vunesp – Funções Matemáticas
- Análise Combinatória no Enem: como cai
- Como calcular porcentagem?
- Binômio de Newton: o que é, como calcular e usos
- Probabilidade no Enem: conceitos e mais
- Progressão aritmética: o que é, fórmulas, usos e exemplos
- Prova de matemática Fuvest 2020 com Resolução Comentada
- Resolução da prova de Matemática da 2ª Fase da Unicamp 2020
- Prova de Matemática UNESP 2020 com Resolução Comentada