Existem diferentes métodos de se calcular áreas de figuras planas, em particular, trato neste artigo sobre a área de triângulo. A maneira de resolver, nesses casos, dependerá dos dados fornecidos pelo problema. Por isso a importância de se ficar atento aos detalhes da questão.
Assim, é importante conhecer o máximo de métodos possíveis de se calcular a área do triângulo. Isso porque, muitas vezes, dependendo dos dados da questão, somente um método pode ser possível. A seguir, o Estratégia Vestibulares listará os casos mais recorrentes nas provas de vestibulares!
Navegue pelo conteúdo
Como calcular área de triângulo?
Área de triângulo: Caso 01
Neste primeiro caso, vamos saber como calcular a área de um triângulo em função dos comprimentos dos lados e suas respectivas alturas. Observe a figura abaixo:
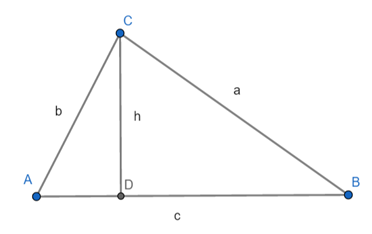
Sejam a, b, c os comprimentos dos lados do triângulo ABC dado e h a altura relativa ao segmento , a área S do triângulo é dada por:
Perceba que um cálculo análogo poderia ser realizado para as demais alturas, atentando sempre para o fato de que a fórmula deve ser escrita respeitando-se a correspondência entre a altura e o respectivo lado.
Esse é o método mais usado. Perceba que você não precisa ter necessariamente todos os lados do triângulo, basta ter um lado e a altura respectiva.
Área do triâgulo: Caso 02
Neste segundo caso, vamos calcular a área do triângulo em função dos cumprimentos dos lados.
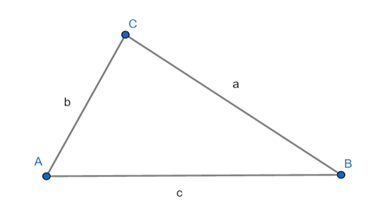
Sejam a, b, c os comprimentos dos lados do triângulo e o semiperímetro do triângulo ABC dado, a área do triângulo é dada por:
A equação acima é conhecida como “fórmula de Heron”, também chamada de “teorema de Herão”.
Perceba que, para este método, são necessários os valores de todos os lados do triângulo.
Área do triângulo: Caso 03
Neste terceiro caso, vamos aprender a calcular a área do triângulo em função dos cumprimentos dos lados e do raio da circunferência inscrita. Observe o triângulo a seguir:
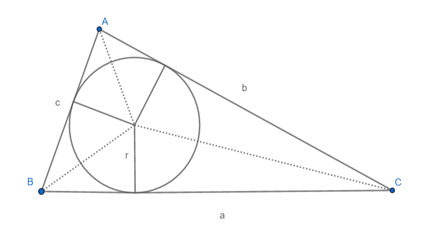
Sejam a, b, c os comprimentos dos lados do triângulo dado, o semiperímetro do triângulo e r o comprimento do raio da circunferência inscrita ao triângulo ABC dado, a área do triângulo em função desses dados é:
Você poderia pensar: por que não usar o método anterior (fórmula de Heron) já que eu tenho os valores de todos os lados do triângulo? Bom, nem sempre a questão vai fornecer todos os lados, o enunciado pode apresentar diretamente o valor do semiperímetro sem ter que citar as medidas dos lados.
Área do triângulo: Caso 04
Aqui, neste quarto caso, vamos calcular a área de triângulo em função dos cumprimentos dos lados e do raio R da circunferência circunscrita. Veja a figura a seguir:
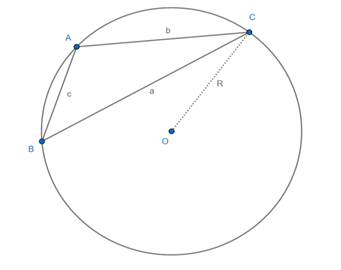
Sejam a, b, c os comprimentos dos lados do triângulo dado e R o comprimento do raio da circunferência circunscrita ao triângulo, a área do triângulo é dada por:
Você pode estar se perguntando: por que não usar o método do 3º caso (fórmula de Heron) já que eu tenho os valores de todos os lados do triângulo?
Veja que para usar a fórmula de Heron você precisa calcular uma raiz e nem sempre a raiz é fácil, e no vestibular normalmente não se pode usar calculadora.
Aí que entra esse método! Se você souber o valor do raio da circunferência externa você poderá encontrar a área fazendo umas contas de multiplicação e divisão. Bem mais fácil que encontrar o valor de uma raiz que nem sempre é raiz perfeita.
Área do triângulo: Caso 05
Neste caso, vamos calcular a área de triângulo em função do raio da circunferência ex-inscrita. Vamos observar a figura a seguir:
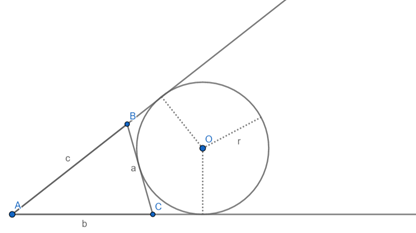
Sejam a, b, c os comprimentos dos lados do triângulo dado, o semiperímetro do triângulo ABC dado e r o comprimento do raio da circunferência ex-inscrita ao triângulo, a área do triângulo é dada por:
Perceba que um cálculo análogo poderia ser realizado utilizando-se as circunferências ex-inscritas aos demais lados, atentando sempre para o fato de que a fórmula deve ser escrita respeitando-se a correspondência entre o lado ao qual a circunferência ex-inscrita é tangente e o raio dessa circunferência.
Esse método é pouco usado, justamente porque é raro encontrar questões que fornecem o valor do raio de uma circunferência ex-inscrita. Mas não deixe de estudar esse método. Nunca se sabe o que a questão vai fornecer!
Área do triângulo: Caso 06
Antes de passar para uma questão de vestibular, vamos calcular a área do triângulo neste último caso. Aqui, vamos aferir a área em função de dois lados e do seno do ângulo compreendido entre esses lados. Observe:
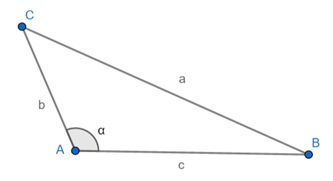
Sejam b, c os comprimentos de dois dos lados do triângulo dado e o valor do ângulo compreendido entre esses dois lados, a área do triângulo é:
Perceba que um cálculo análogo poderia ser realizado utilizando-se combinação de quaisquer dois lados do triângulo e o ângulo compreendido entre eles, atentando sempre para o fato de que a fórmula deve ser escrita respeitando-se a correspondência entre os dois lados e o respectivo ângulo.
Esse método é muito usado também. Nos casos em que a questão fornecer dois lados e o valor do ângulo entre esses lados.
Como área de triângulo cai no vestibular?
Questão ITA 2009
Do triângulo de vértices A, B e C, inscrito em uma circunferência de raio , sabe-se que o lado
mede 2 cm e o ângulo interno
mede 30°. Então, o raio da circunferência inscrita neste triângulo tem o comprimento, em cm, igual a:
a)
b)
c)
d)
e)
Resolução Comentada
A partir das informações do enunciado, podemos construir a seguinte figura:
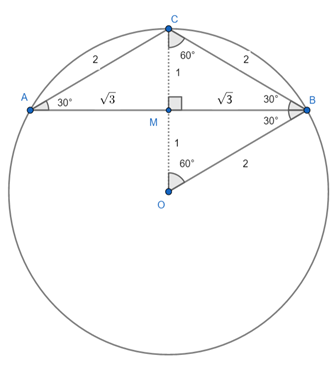
Seja S a área do triângulo ABC, p seu semiperímetro e r o raio da circunferência inscrita ao triângulo, é fácil ver que o problema se encaixa no 1° caso. Portanto, temos:
1)
Podemos calcular a área S de outra maneira também. Veja que ele quer saber o raio da circunferência interna e eu conheço o valor de todos os lados, então é aplicável o método do 3º caso:
2)
Igualando as equações, já que a área é a mesma, temos:
3)
Resposta: D
Note que nessa questão foi necessário saber mais de um método. E não podia ser quaisquer métodos. Você teria que perceber que a questão pedia para encontrar o valor do raio inscrito e logo pensar em usar o método do 3º caso. Bastava pensar em outra maneira de calcular a mesma área. Pode ser tanto o método do 1º caso quanto a fórmula de Heron.




