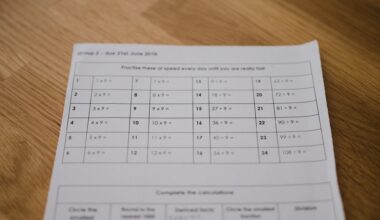
O círculo trigonométrico, também chamado de circunferência trigonométrica ou ciclo trigonométrico, é uma ferramenta matemática que padroniza os valores de ângulos, auxiliando no entendimento das funções seno, cosseno e tangente, por exemplo.
Nas provas de vestibulares, esse assunto sempre aparece: seja com questões de geometria que utilizam ângulos, cálculos trigonométricos, fórmulas de física, no plano cartesiano, entre outras contextualizações. Continue lendo e saiba mais!
Navegue pelo conteúdo
O que é o círculo trigonométrico?
O ciclo trigonométrico é uma figura geométrica circular que, por padrão, possui raio igual a 1. Ele sempre aparece com dois diâmetros marcados, que formam 4 ângulos de 90º entre si.
A partir dessa padronização, foi possível determinar o valor das funções trigonométricas: o senos ficam demonstrados na linha vertical (como se fosse um eixo y do plano cartesiano), enquanto os cossenos estão demarcados na horizontal (semelhante ao eixo das abscissas cartesianas).
A aproximação do plano cartesiano é real: o centro do círculo é considerado o ponto 0,0 da matriz proposta por Descartes. Assim, todos os pontos que estão à esquerda e abaixo do centro possuem valores negativos, veja a imagem abaixo para compreender melhor!
Veja também: Trigonometria: descubra tudo sobre!
Quadrantes do círculo trigonométrico
O ciclo trigonométrico, assim como o plano cartesiano, possui quadrantes que o dividem. A contagem é semelhante em ambos os casos: começando da seção que fica na parte superior direita (I quadrante), em sentido anti-horário, até que se chegue na porção inferior direita (IV quadrante).
Você pode observar, na imagem acima, que o sentido de contagem dos quadrantes influencia na positividade e negatividade dos ângulos. Quando os ângulos estão abertos no sentido anti-horário, serão positivos. Por sua vez, quando abre-se para o sentido horário, são negativos.
Considerando a contagem positiva, entre 0º e 360º, vamos entender a delimitação dos quadrantes em termos de graus:
- O primeiro quadrante está disposto entre 0º e 90º;
- O segundo, fica entre 90º e 180º;
- O terceiro, em seu lugar, relacionado com 180º e 270º;
- Completando a volta, o último e quarto quadrante está posicionado entre 270º e 0º.
Medidas do ciclo trigonométrico
Graus
O círculo trigonométrico trata, principalmente, dos ângulos. É padronizado universalmente que todo o círculo e circunferência possuem em si mesmos, uma volta completa de 360º. A partir desses valores é que são efetuados todos os cálculos trigonométricos.
A soma entre os diversos ângulos dispostos no ciclo deve ser sempre 360º, em se tratando de uma volta completa. Dessa forma, fica fácil entender porque a divisão do círculo trigonométrico em quatro quadrantes iguais determina quatro seções de 90º (90º.4 = 360º).
De maneira semelhante, podemos pensar em um relógio analógico. Como existem 12 partes entre os números que marcam as horas, quais seriam os ângulos entre esses algarismos?
360 ÷ 12 = 30º
Ao mesmo tempo, sabemos que os minutos possuem 60 pequenos pontinhos para serem demarcados. Qual seria a distância angular entre cada um desses pontos?
360 ÷ 60 = 6º
Radianos
Outra unidade utilizada para contabilizar os ângulos é o radiano. Essa padronização é necessária para o desenvolvimento de contas, uma vez que os radianos equivalem aos números comuns, podendo ser manipulados em contas algébricas. Isso é diferente do que acontece com a unidade de graus, que fica restrita a contextos mais geométricos.
A equivalência dos radianos com os graus é tal que π rad = 180º. Assim, por meio da regra de três, observamos que:
π rad —— 180º
x —— 360º (volta completa)
x . 180 = π . 360
x = 360.π /180
x = 2π rad
Alguns estudantes preferem decorar apenas a correspondência π rad = 180 e fazer uso das regras de três para realizar as questões de vestibulares. Outros, optam por saber de cor a equivalência dos ângulos notáveis que foi mostrada acima.
Por uma via ou outra, quanto mais contato você tiver com exercícios que cobrem esse assunto, maior será sua familiaridade com o assunto. Tenha acesso à diversas questões de matemática sobre ciclo trigonométrico no Banco de Questões do Estratégia Vestibulares!
Funções trigonométricas
Como foi citado no decorrer deste artigo, o principal objetivo do ciclo trigonométrico está na relação matemática dos ângulos, por meio das funções trigonométricas. Você pode observar, na figura a seguir, como esses valores são obtidos.
Para encontrar as funções trigonométricas de um ângulo α, traça-se um um raio que determine esse ângulo no ciclo, de modo que:
- A projeção do raio no eixo horizontal é o valor exato do cosseno de α;
- O rebatimento do raio sobre o eixo vertical (y) informa o valor do seno de α; e
- Por fim, a partir de uma tangente que parta do eixo x, o encontro entre a reta tangente e a projeção do raio determina o valor da tangente do ângulo α.
O melhor mnemônico para recordar as duas principais funções, seno e cosseno, é o seguinte: o seno “está em pé”, mas o cosseno “está com sono”, por isso fica deitado.
Veja nos tópicos a seguir as fórmulas que determinam essas funções trigonométricas, e os ângulos notáveis — aqueles que são mais recorrentes no dia a dia, e tem maiores chances de aparecerem nas provas, em termos de todas as ciências exatas.
Fórmulas para as funções trigonométricas
Dado o triângulo retângulo que se forma depois que um ângulo é determinado no círculo trigonométrico, entende-se que são determinados um cateto oposto ao ângulo, uma lado adjacente a ele, e a hipotenusa (que está imediatamente oposta ao ângulo reto). Observe na imagem abaixo.
Com essas informações em mente, observe como cada uma das razões trigonométricas é obtida:
Seno α = cateto oposto / hipotenusa
Cosseno α = cateto adjacente/ hipotenusa
Tangente α = cateto oposto / cateto adjacente
Ângulos notáveis
| sen | cos | tg | |
| 30º | 1/2 | √3/2 | √3/3 |
| 45º | √2/2 | √2/2 | 1 |
| 60º | √3/2 | 1/2 | √3 |
Videoaula gratuita sobre círculo trigonométrico
Veja a resolução de diversas questões sobre trigonometria com a videoaula gratuita abaixo!
Questões de vestibulares: Círculo trigonométrico
IFCE 2014
Considere um relógio analógico de doze horas. O ângulo obtuso formado entre os ponteiros que indicam a hora e o minuto, quando o relógio marca exatamente 5 horas e 20 minutos, é
a) 330º.
b) 320º.
c) 310º.
d) 300º.
e) 290º.
Construído o diagrama acima, para facilitar o entendimento da resolução, vamos nos recordar que a regra de três é uma grande aliada em questões sobre ciclo trigonométrico e seus ângulos.
O primeiro passo a ser observado é que o enunciado se refere ao ângulo obtuso, ou seja, aquele que apresenta mais de 90º, por isso α é o maior ângulo entre os ponteiros.
Vamos imaginar agora que cada um dos ponteiros partiu do ponto 0 horas e 0 minutos, andando certa quantidade de graus até chegar no momento determinado, como foi demonstrado abaixo.
- Para o ponteiro das horas (que completa uma volta a cada 12h):
60.12 min — 360 º
60.5 + 20 min — xº
60.12.x = 360.320
12x=6.320
2x=320
x=160º
- Para o ponteiro dos minutos
60 min — 360 º
20 min — xº
x.60 = 20.360
x = 6.20
x = 120º
Note, então, que os ângulos distam 40º de abertura entre si, estando o ponteiro das horas um pouco mais à frente que a seta dos minutos. O maior ângulo entre eles será dado por:
360 – 40 = 320º, como aponta a alternativa B.
Estude para o vestibular com a Coruja!
Você sabia que o Estratégia Vestibulares fornece questões inéditas comentadas para seus alunos? Os professores de cada disciplina dedicam-se a criar exercícios baseados naqueles que caem na prova, com resolução e guia do raciocínio — isso pode ajudar na construção das respostas no dia do seu exame. Clique no banner e seja também um estrategista!
Veja também:
- Trigonometria: definição e principais conceitos!
- Aproximação sen(x) = tg(x) = xe suas aplicações no vestibular
- Seno, cosseno e tangente: como calcular, tabela e formulas
- Prova de matemática Fuvest 2020 com Resolução Comentada
- Resolução da prova de Matemática da 2ª Fase da Unicamp 2020
- Prova de Matemática UNESP 2020 com Resolução Comentada
- Operações com arcos: o que são, ciclo trigonométrico e como fazer
- Funções trigonométricas: fórmulas, gráficos e aplicações