Na algébrica, as expressões matemáticas podem ser divididas conforme o conjunto de números que abrangem, qual o maior expoente presente ou outros critérios. Um exemplo de classificação é a equação irracional, que acontece quando a incógnita está dentro de uma raiz quadrada.
No artigo a seguir, você entenderá melhor como resolver uma equação irracional, com todos os parâmetros que devem ser levados em consideração, como as questões de valores positivos e negativos, tão importantes para a radiciação. Continue lendo!
Navegue pelo conteúdo
O que é uma equação irracional?
Como foi citado anteriormente, a equação irracional acontece quando o “x” apresenta-se, pelo menos uma vez, como radicando de uma raiz de índice n. Veja um esquema sobre esses elementos que compõem uma radiciação:
- O elemento de número 1 (n) é o índice da fórmula radical. Quando se fala de raiz quadrada, o n=2. Nos casos em que a raiz é cúbica n=3 e assim sucessivamente;
- Já o que está marcado em verde (2) representa o símbolo gráfico da raiz matemática; e
- Por fim, o que está em azul (3) é o radicando dessa operação. Esse componente pode possuir interações de soma, subtração, divisão ou multiplicação.
É importante lembrar que o símbolo da radiciação (√) indica que devemos fatorar um radicando e chegar em um valor que, quando multiplicado n vezes, resulta em x.y. Outro ponto a destacar é que quando o valor de n não está explícito na expressão, indica que n=2.
Um número sob uma raiz matemática é o inverso da potenciação, quando adicionamos um expoente ao n. Assim, a operação também pode ser descrita como:
Para decorar essa propriedade fundamental da radiciação e potenciação, pode ser usado um macete. Primeiramente, imagine que a raiz é uma festa e que o x4 está na festa, enquanto o 2 não foi convidado. Então você faz o expoente da seguinte maneira: “quem está fora da festa ‘está por baixo’, quem tá na festa ‘tá por cima’”.
Com essas informações concluímos que a expressão genérica para uma equação irracional é o aparecimento de um termo com raiz enésima (n), onde esteja a incógnita. É necessário ressaltar que outras operações matemáticas podem acontecer dentro dessa mesma raiz, ou fora dela, como mostram os modelos abaixo descritos.
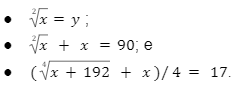
Como resolver uma equação irracional?
Nos tópicos a seguir, você encontrará a resolução de exercícios de vestibulares sobre equação irracional. Observe os passos abordados na resposta para entender como se resolve uma equação com raiz quadrada, cúbica, entre outras.
(UTFPR – adaptado) A equação irracional abaixo resulta em x igual a:
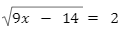
a) – 2
b) – 1
c) 0
d) 1
e) 2
Para desenvolver uma equação irracional, é necessário fazer com que a raiz “suma” dos cálculos. Para isso, utilizamos o princípio da equivalência, quando isolamos a incógnita radicalar e, depois, adicionamos o expoente n em toda a expressão — o que desaparece com a raiz, conforme as propriedades da radiciação.
Na equação do exercício da UFTPR, o n=2, então é possível realizar as seguintes manipulações:
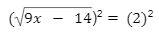
Com o mesmo raciocínio podemos, agora, eliminar a raiz quadrada e continuar os cálculos na equação irracional. Não se esqueça de realizar o jogo de sinais para transferir os elementos de um lado para o outro na expressão!
9x – 14 =4
9x = 4 + 14
9x = 18
x = 18/9
x = 2
A partir dos cálculos que efetuamos, podemos considerar que a alternativa correta para esse exercício é a letra E.
Veja, com auxílio de uma questão que também apareceu no vestibular da UFTPR, como compreender relacionar a equação irracional com os problemas propostos em prova.
Adriana e Gustavo estão participando de uma gincana na cidade de Curitiba e receberam a seguinte tarefa:
Trazer a fotografia da construção localizada na rua XV de Novembro, número N, tal que:
a e b são as raízes da equação irracional
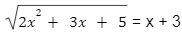
e N = (a2 + b2 + 13)2 + (a + b)4 – 10.
a) 1515.
b) 1296.
c) 971.
d) 775.
e) 535.
O primeiro passo é aplicar o Princípio da Equivalência, dessa forma:
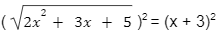
2x2 + 3x + 5 = x2 + 2.x.3 + 32
2x2 + 3x + 5 = x2 + 6x + 9
2x2 – x2 + 3x – 6x + 5 – 9 = 0
x2 – 3x – 4 = 0
A equação x2 – 3x – 4 = 0 está dentro do padrão mx2 + px + c = 0, de forma que:
m = 1
p = -3
c = -4
Pela resolução das equações de segundo grau pelo método da soma e dos produtos, teremos que:
a + b = -p/m e a.b = c/m
a + b = – (-3)/1
a + b = 3
a.b = -4/1
a/b = -4
Com a resolução de um sistema de duas incógnitas e duas equações, teremos que:
a = 3 – b
Substituindo o valor de a na equação a/b = -4, teremos:
(3-b)/b = -4
3 – b = -4.b
3 = -4.b + b
3 = -3.b
b = -1
Como sequência, entende-se que:
a = 3 – b
a = 3 – (-1)
a = 3 + 1
a = 4
Com a parte da equação irracional já resolvida, deve-se prosseguir o raciocínio com a resolução da expressão de N, utilizando-se a=4 e b=-1.
N = (a2 + b2 + 13)2 + (a + b)4 – 10.
N = (42 + (-1)2 + 13)2 + (4 + (-1))4 – 10
N = (16 + 1 + 13)2 + (4 -1)4 – 10
N = 302 + 3 4 – 10
N = 900 + 81 – 10
N = 971, como prevê a alternativa de letra C.
Números positivos ou negativos no radicando
Para que um número negativo esteja presente no radicando de uma raiz enésima, é necessário que n seja um número ímpar. Quando n é par, os valores presentes no radicando devem ser, obrigatoriamente positivos, para que estejam no conjunto dos números reais. Veja:
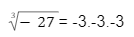
O exemplo acima demonstra que, um número negativo, quando multiplicado por si mesmo em fatores ímpares, resulta em um valor negativo. Entretanto, se multiplicarmos esse mesmo número em vezes pares, o resultado será maior que 0:
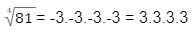
Por essa razão, também, as equações irracionais com n par possuem uma raiz positiva e outra negativa que solucionem sua incógnita.
Aprenda mais matemática com a Coruja!
Com as aulas gratuitas fornecidas pelo Estratégia Vestibulares no YouTube você pode aprimorar seu conhecimento matemático e agilizar o seu raciocínio no desenvolvimento dos cálculos.
Além de assistir nossos conteúdos gratuitos, confira o Banco de Questões desenvolvido pela Coruja. Nessa ferramenta você encontra os principais exercícios de matemática que já caíram nos vestibulares como Enem, USP, Unicamp e Unifesp. Quer saber mais? Clique no banner abaixo!