No decorrer da história da humanidade, os indivíduos adquiriram uma sensibilidade à ideias como os formatos dos edifícios, a criação de vestimentas e todo estudo sistemático das proporções corporais com uso de figuras geométricas, tanto as planas como as não planas. Essas percepções iniciais originaram os conhecimentos atuais sobre as mais diversas áreas.
Dada a forte relação entre a geometria e os variados domínios do conhecimento, percebe-se a importância desse assunto para os vestibulares. Por essa razão, a Coruja preparou um resumo com as principais informações sobre o que são as figuras geométricas e como elas aparecem nas provas. Confira!
Navegue pelo conteúdo
O que são as figuras geométricas?
As figuras geométricas são estruturas que possuem dimensões, formato definido, tamanho e estão dispostas em um espaço ou plano. Para compreender melhor a questão do dimensionamento dos elementos matemáticos no espaço, acompanhe os tópicos a seguir:
- Zero dimensão: é a condição em que o elemento não possui nenhuma dimensão significativa. O principal exemplo é o ponto geométrico, que não pode ser mensurado com largura, altura ou profundidade;
- Uma dimensão: as retas, semirretas e segmentos de retas são estruturas que possuem apenas uma dimensão, o comprimento;
- Duas dimensões: os principais representantes desse tópico são os polígonos (quadrado, triângulo, retângulo). Eles possuem comprimento e altura mas não são dimensionados em profundidade;
- Três dimensões: são figuras geométricas que contêm as três dimensões mensuráveis — comprimento, largura e altura — como o cubo, a esfera, o cone e outros exemplos.
Em meio a essas definições, existem as figuras geométricas planas e aquelas que não são planas, como será apresentado nos parágrafos seguintes. Acompanhe!
Figuras geométricas planas
Como dito anteriormente, as chamadas figuras geométricas planas possuem apenas duas dimensões quantificáveis. Veja alguns exemplos na figura abaixo:
A compreensão de seus formatos permite a distribuição delas em dois subgrupos principais, os polígonos e não polígonos, veja:
Polígonos
São figuras fechadas e compostas por diversos segmentos de reta interligados em algum ponto. É importante notar que os lados não podem cruzar-se entre si.
Agora que você já sabe o que é um polígono, é importante entender que existem duas classificações distintas:
- Convexos: são figuras geométricas em que, ao desenhar um segmento de reta que começa e acaba no interior do polígono, não há porções exteriores desse segmento;
- Côncavos: são assim definidos quando, ao traçar um segmento de reta que se inicia e termina no interior da figura, uma parte desse segmento ficou exterior ao polígono.
Compreenda melhor com a imagem:
Ainda sobre polígonos, conheça as nomenclaturas dos polígonos conforme o número de lados que possuem:
| Nomenclatura | Número de lados |
| Triângulo | 3 |
| Quadrilátero | 4 |
| Pentágono | 5 |
| Hexágono | 6 |
| Heptágono | 7 |
| Octógono | 8 |
| Eneágono | 9 |
| Decágono | 10 |
| Undecágono | 11 |
| Dodecágono | 12 |
| Icoságono | 20 |
Figuras planas curvas
Os formatos geométricos que apresentam duas dimensões mas possuem lados curvos, são considerados figuras planas curvas.
Nesse caso, o exemplo mais comum é o círculo. A quantificação e medidas geométricas são obtidas por meio raios, diâmetros, medidas de circunferência e outras ferramentas matemáticas que são utilizadas quando as retas estão ausentes.
Na imagem acima, embora a figura violeta apresenta segmentos de retas como lados, existem porções curvas na silhueta do elemento. Assim como na figura rosa, em que há um único lado curvo. Esses fatores são suficientes para determinar que não são polígonos, mas figuras geométricas planas do tipo curvas.
Figuras geométricas não planas
Além dos formatos planificados, existem as figuras geométricas não planas: elas possuem três dimensões quantificáveis e ocupam lugar significativo no espaço. Por isso, são chamadas também de figuras espaciais.
Assim como no tópico anterior, os sólidos geométricos são classificados conforme os seguintes exemplos:
Poliedros
São figuras espaciais nas quais todas as superfícies são planas e as arestas são representadas por segmentos de reta. Como exemplo pode-se citar o cubo, o paralelepípedo, as pirâmides, os tetraedros, entre outros.

Não Poliedros
Por outro lado, os sólidos geométricos que apresentam pelo menos uma superfície curva são chamados de não poliedros. Por exemplo o cilindro, a esfera, o cone, e outros exemplos.
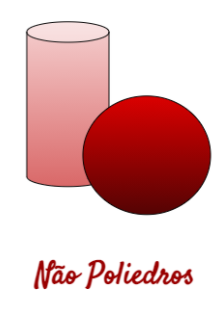
Importância das figuras geométricas
Apesar de parecerem ideias abstratas e restritas ao estudo matemático, as figuras geométricas estão totalmente relacionadas com o nosso cotidiano.
Quando utilizam-se cartografias, plantas de imóveis, desenhos esquemáticos, formatos bidimensionais na decoração de casas e outras situações, constroem-se relações importantes entre figuras planas e as necessidades humanas.
No caso das figuras geométricas espaciais, essa interação é mais marcante: o formato de um dado, a criação de maquetes tridimensionais, a casca do sorvete, os potes de cozinha e diversos objetos marcam a presença da geometria no dia a dia.
Matematicamente, é importante calcular a área das superfícies, o volume da figura, o espaço que ela ocupa e outras grandezas. Com isso, pode-se obter a massa, densidade e outros valores significativos para outros domínios da ciência, como a física e a química.
Essas associações estão muito presentes em questões sobre figuras geométricas no Enem e outros vestibulares, confira no tópico seguinte.
Questão de Figuras Geométricas
ENEM 2016
Uma família resolveu comprar um imóvel num bairro cujas ruas estão representadas na figura. As ruas com nomes de letras são paralelas entre si e perpendiculares às ruas identificadas com números. Todos os quarteirões são quadrados, com as mesmas medidas, e todas as ruas têm a mesma largura, permitindo caminhar somente nas direções vertical e horizontal. Desconsidere a largura das ruas.
A família pretende que esse imóvel tenha a mesma distância de percurso até o local de trabalho da mãe, localizado na rua 6 com a rua E, o consultório do pai, na rua 2 com a rua E, e a escola das crianças, na rua 4 com a rua A.
Com base nesses dados, o imóvel que atende as pretensões da família deverá ser localizado no encontro das ruas
a) 3 e C
b) 4 e C
c) 4 e D
d) 4 e E
e) 5 e C
Na planificação representada na imagem, é importante anotar cada ponto citado no enunciado. Com isso, percebe-se que no ponto azul existe um cruzamento de ruas que dista 3 quarteirões tanto do consultório do pai, do trabalho da mãe e da escola das crianças. Desse modo, a melhor alternativa é a letra c — encontro das ruas 4 e D.
Assista uma aula grátis de Figuras geométricas
Aprenda mais de geometria ao acompanhar o canal do Estratégia no youtube:
Precisa treinar seu conhecimento matemático, mas não sabe onde encontrar exercícios? Clique no banner abaixo e conheça o banco de questões do Estratégia Vestibulares, lá você encontrará diversas perguntas que já apareceram nas provas e te ajudarão na construção do aprendizado. Aproveite!
Veja também:
- Geometria: o que é e como é classificada
- Geometria Plana no Enem: conceito e definições
- Triângulos: definição, perímetro, área, classificações
- Semelhança de triângulos
- Círculo e circunferência: conceitos e exercícios
- Geometria analítica: fórmulas, gráficos e equações
- Geometria Espacial: conheça os sólidos e fórmulas
- Teorema de Pitot: o que diz o teorema e como é cobrado em prova
- Área do trapézio: conheça a fórmula e como calcular!
- Prova FUVEST 2020 – Matemática – Resolução Comentada
- Resolução da prova de Matemática da 2ª Fase da Unicamp 2020
- Prova UNESP 2020 – Matemática – Resolução Comentada




