Navegue pelo conteúdo
O que é plano cartesiano?
O Plano Cartesiano é como uma tela onde cada ponto tem seu endereço. Para chegar a um ponto qualquer dessa tela, deslocamo-nos a partir da origem primeiro na horizontal (direita ou esquerda) e, depois, na vertical (para cima ou para baixo). O Estratégia Vestibulares traz você tudo sobre essa tela!
Para simbolizar esse “deslocamento”, escreveremos os endereços sempre nesta ordem: horizontal e vertical. Por isso chamamos esses endereços de coordenadas dos pontos de pares ordenados. Chamaremos, de agora em diante, as coordenadas horizontais de abscissas e as coordenadas verticais de ordenadas.
Embora possamos utilizar quaisquer símbolos para, algebricamente, representar um par ordenado, há grande preferência para as letras ? e ? para representar as abscissas e as ordenadas, respectivamente.
Desse modo, (2; 3) indica um ponto a duas unidades de distância horizontal e três de distância vertical a partir da origem de um plano cartesiano, enquanto (?; ?) é uma representação para um par ordenado genérico.
Quando não causar confusão com números decimais não inteiros, podemos representar pares ordenados separados por vírgula, ao invés de ponto e vírgula, (?, ?), sem prejuízo para a clareza e correção da notação.
Vejamos com o representar essas coordenadas no plano cartesiano. Perceba que os eixos dividem o plano em quatro regiões, chamadas quadrantes.
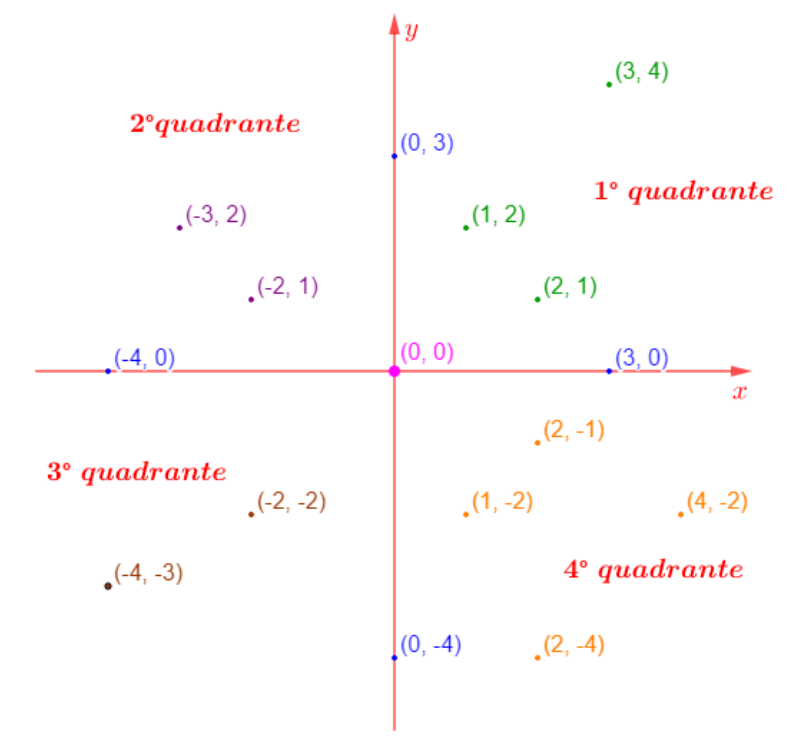
Alguns detalhes que gostaria que você notasse e os observasse sempre que vir um plano cartesiano a partir de agora:
- Números positivos e negativos, nos eixos, são divididos pelo ponto (0,0).
- As setas, rigorosamente expressas em apenas uma das extremidades de cada eixo, indicam o sentido de crescimento dos números e não, não podem ser colocadas em ambas as extremidades, ok?
- Os números que estão exatamente em cima de um eixo coordenado sempre têm uma das coordenadas igual a zero. Se o ponto está no eixo ?, tem a coordenada ? = 0. Se o ponto está no eixo ?, tem sua coordenada ? = 0. Essa característica será muito útil em toda a nossa jornada na matemática!
Como cai Plano Cartesiano em prova?
Questão Unesp/2019
Em relação a um sistema cartesiano de eixos ortogonais com origem em ?(0,0), um avião se desloca, em linha reta, de ? até o ponto ?, mantendo sempre um ângulo de inclinação de 45° com a horizontal. A partir de ?, o avião inicia trajetória parabólica, dada pela função ?(?) = −?² + 14? − 40, com ? e ?(?) em quilômetros. Ao atingir o ponto mais alto da trajetória parabólica, no ponto ?, o avião passa a se deslocar com altitude constante em relação ao solo, representado na figura pelo eixo ?.
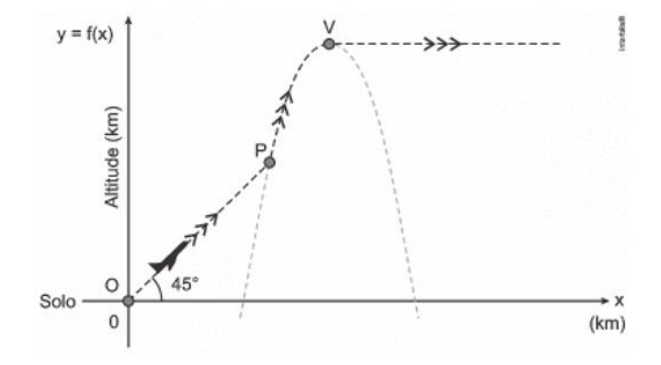
Em relação ao solo, do ponto ? para o ponto ?, a altitude do avião aumentou:
a)
b)
c)
d)
e)
Resolução Comentada
O encontro entre a trajetória retilínea e a parabólica ocorre quando
Altura do ponto P:
Altura máxima, vértice da parábola:
Assim, a diferença entre a altura do ponto P e a altura máxima da parábola é dada por:
Gabarito: D
Veja também:
- Geometria: o que é e como é classificada
- Figuras Geométricas: planas, espaciais e como aparece nos vestibulares
- Geometria Plana no Enem: conceito e definições
- Semelhança de triângulos
- Círculo e circunferência: conceitos e exercícios
- Geometria analítica: fórmulas, gráficos e equações
- Geometria Espacial: conheça os sólidos e fórmulas
- Área do trapézio: conheça a fórmula e como calcular!
- Arcos e ângulos: o que são, circunferência e como medir
- Retas: o que são, geometria, classificação e aspectos gerais




