Probabilidade da união, probabilidade da intersecção e probabilidade complementar são subtipos de cálculos probabilísticos essenciais para o estudo estatístico, desenvolvimento de dados e estratégias para a vida cotidiana, seja para criação de estratégias políticas, análise do desenvolvimento econômico, cálculos demográficos, entre outros exemplos.
Neste artigo, aprofunde seu conhecimento sobre probabilidade de um evento complementar, com sua definição e as fórmulas necessárias para o cálculo. Veja também um exemplo prático de resolver um problema de provas de vestibulares sobre o tema. Vamos lá?
Navegue pelo conteúdo
Definição de probabilidade complementar
Probabilidade pode ser definida como a chance de um evento A ocorrer, dado um conjunto de S situações possíveis, esse conjunto S é chamado de espaço amostral, demonstrado pela fórmula
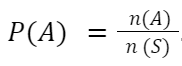
O evento A deve estar contido dentro do espaço amostral, por exemplo, em qual a chance de aparecer um número par, ao lançamento de um dado de seis lados? O dado possui 3 números pares ao todo: 2, 4 e 6. Então, o número de elementos que satisfazem o evento A é n(A) = 3, enquanto que o espaço amostral é dado por todos os números possíveis de serem obtidos no lançamento (1, 2, 3, 4, 5 e 6), n(S) = 6.
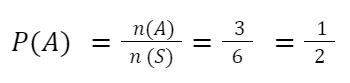
Tomado esse exemplo, note que o espaço amostral sempre terá um valor maior ou igual ao numerador. Assim, o valor de uma probabilidade sempre varia entre 0 e 1, de forma que 0 significa que existe 0% de A ocorrer e 1 indica que A ocorrerá em 100% das vezes.
O cálculo de uma probabilidade depende sempre da inclusão de alguns eventos que satisfazem o critério de A, enquanto que outros elementos do espaço amostral são excluídos da conta de n(A). No exemplo acima, os números pares 2, 4 e 6 satisfazem o evento A, enquanto que os valores ímpares do espaço amostral (1, 3 e 5) são considerados um evento complementar de a (AC). Então, a probabilidade complementar do enunciado acima é dada por P(AC).
Como é calculada a probabilidade complementar?
Para calcular a probabilidade complementar de um evento é possível utilizar a fórmula a seguir:
P(AC) = 1 – P(A)
Observe que esse cálculo evidencia que a probabilidade complementar do evento A é exatamente a probabilidade do evento A não acontecer, ou seja.
Ou ainda, é possível calcular a probabilidade de um evento complementar determinando qual o conjunto de elementos complementares e, assim, aplicando a fórmula de probabilidade simples:
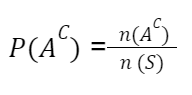
Como resolver e interpretar probabilidade complementar?
Um mercado está sorteando um carro para seus clientes, todos os compradores que fizeram mais de dois mil reais em compras no mês de novembro devem retirar uma bolinha da urna, que contém 100 bolas, numeradas de 1 a 100. Os consumidores que conseguirem um número maior do que 75 serão selecionados para o sorteio final do carro. João e seu vizinho Pedro vão retirar um número na urna, João quer saber qual a chance de Pedro não ser selecionado para o sorteio final.
Observe que o enunciado fornece um evento A, que é a retirada de um número maior do que 75. Entretanto, a probabilidade que foi pedida é a chance de Pedro não ser selecionado, ou seja, de não ocorrer o evento A, uma probabilidade complementar.
O primeiro passo para resolver esse tipo de problema é determinar qual o evento A e seus elementos, bem como o conjunto de elementos do evento complementar AC:
- A possui todos os números maiores que 75. Observe que o número não está incluso, então o conjunto inicia-se com 76;
- AC são todos os elementos de 1 até 75, com o número 75 incluso, uma vez que, se retirar o número 75 ele não seleciona o candidato para o sorteio final.
A probabilidade de AC acontecer pode ser calculada a partir de uma fórmula direta, contando o número de elementos do conjunto AC:
n(AC) = 75
n (S) = 100 (número total de bolinhas)
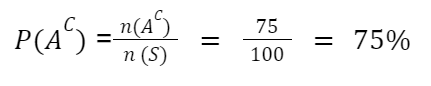
A probabilidade complementar do evento A é dada por 75%, ou seja, há 75% de chances de Pedro não passar para a próxima etapa do sorteio.
Agora, imagine que o enunciado apresenta o mesmo problema e quer saber, independentemente:
- a chance de João estar entre os selecionados;
- a chance de Pedro estar entre os não selecionados.
Nessa nova situação, é preciso calcular também a probabilidade do evento A acontecer com João, então:
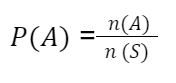
O conjunto A possui n(A) = 25 elementos, de forma que:
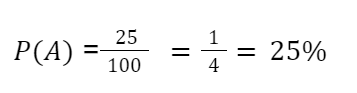
Então, João tem 25% de chance de estar entre os candidatos finais ao sorteio do carro.
Agora, precisamos saber qual a chance de Pedro não estar nessa lista. Como já sabemos qual a chance do evento A acontecer, a chance deste evento não acontecer pode encontrada por:
P (não ir para o evento final) = todas as situações possíveis – (P ir para o evento final)
Basicamente, essa é a outra fórmula da probabilidade complementar:
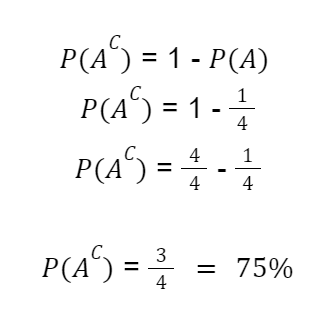
Note que, independentemente da fórmula utilizada, a probabilidade complementar teve o mesmo valor.
Questão de probabilidade no Enem
O exercício abaixo, do Enem 2017, relaciona o conhecimento de probabilidade complementar com outros aspectos do estudo probabilístico. Acompanhe o enunciado, tente resolver e depois veja a resolução completa proposta pela professora Luciana Fagundes, docente do Estratégia Vestibulares.
Um programa de televisão criou um perfil em uma rede social, e a ideia era que esse perfil fosse sorteado para um dos seguidores, quando esses fossem em número de um milhão. Agora que essa quantidade de seguidores foi atingida, os organizadores perceberam que apenas 80% deles são realmente fãs do programa. Por conta disso, resolveram que todos os seguidores farão um teste, com perguntas objetivas referentes ao programa, e só poderão participar do sorteio aqueles que forem aprovados. Estatísticas revelam que, num teste dessa natureza, a taxa de aprovação é de 90% dos fãs e de 15% dos que não são fãs.
De acordo com essas informações, a razão entre a probabilidade de que um fã seja sorteado e a probabilidade de que o sorteado seja alguém que não é fã do programa é igual a é igual a.
a) 1.
b) 4.
c) 6.
d) 24.
e) 96.
Probabilidade de que um fã seja sorteado (𝑃₁):
– Casos favoráveis: 𝑠𝑒𝑟 𝑓ã (0,8) 𝑥 𝑠𝑒𝑟 𝑎𝑝𝑟𝑜𝑣𝑎𝑑𝑜 (0,9) = 0,8.0,9
– Casos possíveis de serem sorteados:
𝑠𝑒𝑟 𝑓ã (0,8) 𝑥 𝑠𝑒𝑟 𝑎𝑝𝑟𝑜𝑣𝑎𝑑𝑜 (0,9) 𝑜𝑢 (+) 𝑛ã𝑜 𝑠𝑒𝑟 𝑓ã (0,2)𝑥 𝑠𝑒𝑟 𝑎𝑝𝑟𝑜𝑣𝑎𝑑𝑜 (0,15) = 0,8.0,9 + 0,2.0,15
Probabilidade de que um não fã seja sorteado (𝑃₂): 1−𝑃₁
Assim:
Alternativa correta: D.
Estude com o Estratégia Vestibulares
No curso preparatório da Coruja, você poderá aprender com profundidade as matérias exatas, um ponto de grande interesse para os vestibulandos. Além disso, o Estratégia fornece aulas, simulados e trilhas estratégicas que te ajudam na programação e avaliação do conhecimento em todas as disciplinas mais importantes para os vestibulares nacionais. Quer saber mais? clique no banner abaixo:




