A radiciação é uma operação matemática que aparece com muita frequência nos vestibulares: diversos exercícios de equações ou problemas pedem a resolução de uma raíz quadrada, ou a inversão de uma potência. Esses assuntos são todos pertinentes à radiação, o que torna o tema extremamente relevante no estudo preparatório.
Neste artigo, você entenderá melhor a relação entre as raízes quadradas e as potências, quais são as propriedades e símbolos da radiciação, além de ver exemplos de questões do vestibular que abordam o tema. Continue lendo e conheça mais!
Navegue pelo conteúdo
O que é radiciação?
A radiciação pode ser definida pela operação inversa da potenciação. Isso significa que, quando operamos uma radiciação em um elemento com expoente, encontra-se um valor neutro. O símbolo matemático para a radiciação é a raiz (√), como você observa na imagem abaixo.
O número n (em vermelho) que aparece na lateral esquerda da raiz é o índice, responsável por dar nome a ela. A mais comum é a raiz quadrada, que pode ser representada tanto por 2√ ou √ (sem o número dois).
Existem outros tipos de raiz, como a raiz cúbica (3√), raiz quarta (4√), raiz quinta (5√) e assim sucessivamente.
Em verde está evidenciado o símbolo da radiciação e, em azul (3), encontramos o radicando: valor que fica dentro da raiz e será operado
Agora que você já entende melhor o símbolo e a localização dos elementos em uma radiciação, veja o que essa operação significa em termos matemáticos:
an = x ⇒ n√x = a
Veja: a potência multiplica o elemento a n vezes, resultando no valor x.
Enquanto isso, a radiciação serve para encontrar o valor que, multiplicado n vezes, resulta em x. Dessa forma, na equação 2√16 = y, você quer descobrir um y que, multiplicado por si mesmo 2 vezes, resultará em dezesseis:
2√16 = y ⇒
⇒ y2 = 16
⇒ y.y= 16
⇒ y = 4
Propriedades da radiciação
Inversa da potência
A primeira propriedade da radiciação já foi abordada no tópico anterior: a radiciação é a operação inversa da potenciação. Inclusive, existe uma forma de escrever as raízes apenas com expoentes, sem o símbolo clássico, assim:
n√xy = xy/n
Veja que, o radicando x tem o expoente y, e o valor do índice é n. Quando transformamos essa estrutura em uma potência, o expoente será fracionário.
Essa fração será tal que: o expoente do radicando (y) fica na parte de cima da fração (numerador), enquanto o índice da raiz fica na parte de baixo (denominador).
Essa configuração pode ser lembrada com a seguinte ideia: imagine uma festa, as pessoas que estão no dentro do camarote estão “por cima”, quem só vê de fora está “por baixo”. Então, o que está dentro da raiz fica por cima, o que está fora, fica por baixo.
10√45 = 45/10
7√32 = 32/7
4√82 = 82/4
Multiplicação e divisão do expoente e índice
A segunda propriedade da radiciação é que, quando o índice e o expoente do radicando são multiplicados pelo mesmo valor, o resultado do cálculo não se altera, assim:
n√xy = n.a√xy.a
2√26 = 3.2√23.6
Uma consequência dessa propriedade é que, o expoente do radicando e o índice podem ser divididos pelo mesmo valor, até mesmo para facilitar os cálculos. Geralmente, isso será feito até encontremos o primeiro número primo seja no expoente ou no índice da raiz, vejamos:
3.2√23.6 = x
6√218 = x
Como o 6 e o 18 têm divisores em comum, podemos operá-los com esses divisores, até que fiquem no menor valor possível:
6√218 = x
6 ፥ 2√218 ፥ 2 = x
3√29 = x
Se utilizarmos o conceito da radiciação nesse estágio da equação, já podemos encontrar o valor de x, observe:
3√29 = x ⇒ x3 = 29
Agora, utilizando as propriedades da potenciação, sabemos que na multiplicação de potências, operamos uma soma dos expoentes:
x3 = 23+3+3
x3 = 23.23.23
x3 = 8.8.8
Assim, x=8
Multiplicação e divisão de raízes com o mesmo índice
A terceira propriedade versa sobre raízes de mesmo índice que estão sendo multiplicadas ou divididas.
Quando isso acontece, podemos colocá-las todas embaixo de um mesmo símbolo de raiz, realizando apenas a operação multiplicativa ou fracionária, assim:
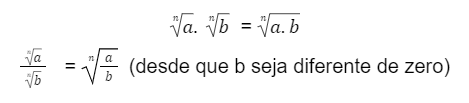
Acompanhe os exemplos:
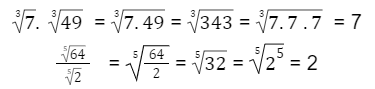
Expoente da raiz toda é um expoente do radicando
Quando uma raiz está toda exponenciada por um valor n, isso pode ser reescrito com o mesmo expoente n somente no radicando, assim:
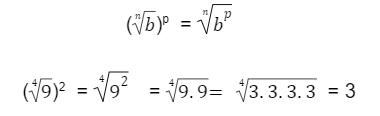
Inclusive, caso você encontre uma radiciação em que o índice é igual ao expoente interno, o resultado dessa conta é o próprio radicando:
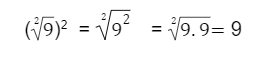
E quando uma raiz está dentro da outra?
A última propriedade a ser abordada são os casos em que precisa-se calcular a raiz da raiz. Nesse caso, o radicando é conservado e os índices devem ser multiplicados, da seguinte maneira:
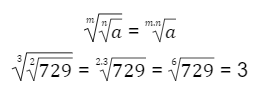
Como encontrar o valor de uma raiz?
Agora que você já conhece as principais propriedades da radiciação, vamos treinar esse conhecimento aplicando na resolução de um exercício. Aprenda, então, como encontrar o valor de uma raiz!
O primeiro passo é sempre fatorar (dividir) o número em número primos, até que se encontre o valor de 1. Assim, você encontra uma grande multiplicação que resume aquele valor. Depois, você agrupa eles em grupinhos de n elementos, considerando que n é o índice da radiciação em questão.
O número de grupos com n elementos é o resultado do cálculo.
√625 = ?
625 ፥ 5 = 125 ፥ 5 = 25 ፥ 5 = 5 ፥ 5 = 1
Assim, são necessárias quatro multiplicações de 5 por ele mesmo para encontrar o valor de 625. Ou seja:
√625 = 5.5.5.5, podemos simplificar esse processo como:
√625 = 52.52
O número que, multiplicado por si mesmo duas vezes resulta em 625 é o 52 = 25
Questão de vestibular sobre radiciação
(CEFET/RJ) Por qual número devemos multiplicar o número 0,75 de modo que a raiz quadrada do produto obtido seja igual a 45?
a) 2700.
b) 2800.
c) 2900.
d) 3000.
√(0,75.x) = 45
452 = 0,75.x
2025 = 0,75 . x
2025 / 0,75 = x
x = 2700, como aponta a alternativa A.
Aprenda mais com o Estratégia Vestibulares!
Quer ter acesso a diversas questões comentadas a passo a passo, além de poder tirar dúvidas da resolução a qualquer momento em um fórum de dúvidas com professores especialistas? Conheça os cursos da Coruja. Cursos focados na prova dos seus sonhos, material didático está disponível em pdf, online e em aulas gravadas ou ao vivo, no canal do YouTube do Estratégia Vestibulares. Clique no banner e saiba mais!
Veja também:
- Moda, média, mediana: o que é e como cai no vestibular?
- Regra de três simples e composta: veja como calcular
- Análise Combinatória no Enem: como cai
- Como calcular porcentagem?
- Binômio de Newton: o que é, como calcular e usos
- Probabilidade no Enem: conceitos e mais
- Progressão aritmética: o que é, fórmulas, usos e exemplos
- Radiciação: o que é, propriedades, potências e exemplos
- Prova de matemática Fuvest 2020 com Resolução Comentada
- Resolução da prova de Matemática da 2ª Fase da Unicamp 2020
- Prova de Matemática UNESP 2020 com Resolução Comentada




