Resolução da prova de Física Unicamp 2ª Fase 2020

Fala, pessoal. Tudo certo? Sou o prof. Lucas Costa, professor de Física do Estratégia Vestibulares. Escrevo este artigo para, juntos, resolvermos as questões da prova de Física da UNICAMP 2020, 2ª Fase do Vestibular. Vamos nessa?

Navegue pelo conteúdo

Questão 11

Estudos indicam que uma massa $\dpi{100} \large m=1000\ kg$ de poeira cósmica, composta por minúsculas partículas, colide com a superfície da Terra a cada intervalo $\dpi{100} \large \Delta t=20 min$ . Considere, para simplificar, que as partículas de poeira têm velocidade média nula antes de serem arrastadas pela Terra no seu movimento em torno do Sol. Logo após colidirem com a superfície do nosso planeta, elas passam a se deslocar juntamente com a Terra, com velocidade média de módulo igual a $\dpi{100} \large v_{Terra}=30\ km/s$ . Considere também que o movimento da Terra num intervalo $\dpi{100} \large \Delta t=20 min$ é retilíneo e uniforme.

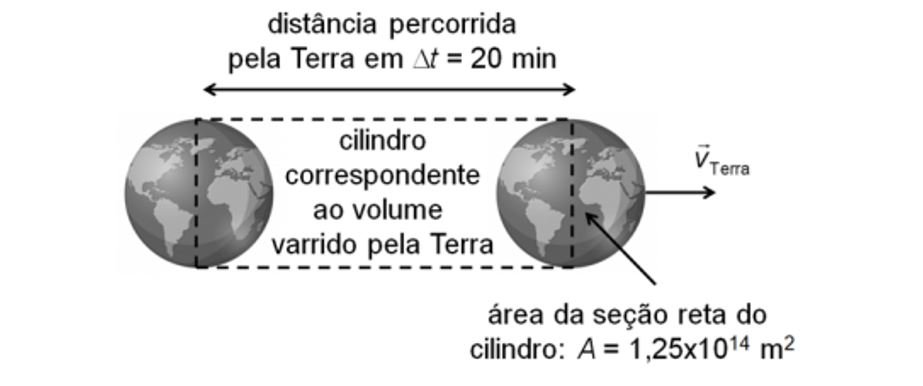
a) Qual é a densidade da poeira na região do espaço atravessada pela Terra? Ver ilustração ao lado.

b) Qual é o módulo da força média aplicada pela Terra sobre a massa de poeira cósmica que ela intercepta durante um intervalo ∆t=20 min?

a) A densidade da poeira é dada pela razão entre a sua massa e o volume por ela ocupado. A massa é fornecida e o volume pode ser calculado pelo produto entre a área da seção reta e a sua altura, que é a distância percorrida pelo planeta no intervalo de tempo fornecido:

$\dpi{100} \large v=\frac{\Delta S}{\Delta t}\Rightarrow \Delta S=h=v_{Terra}\cdot \Delta t$

$\dpi{100} \large h=30\cdot{10}^3\cdot20\cdot60=36\cdot{10}^6\ m$

Agora podemos calcular o volume do cilindro correspondente ao volume varrido pela Terra:

$\dpi{100} \large V_{cilindro}=A_{base}\cdot h$

$\dpi{100} \large V_{cilindro}=1,25\cdot{10}^{14}\cdot36\cdot{10}^6=45\cdot{10}^{20}\ m^3$

Finalmente, podemos calcular a densidade da poeira espacial:

$\dpi{100} \large d=\frac{m}{V}$

$\dpi{100} \large d=\frac{1000}{45\cdot{10}^{20}}=22,2\cdot{10}^{-20}$

$\dpi{100} \large d=2,\bar{2}\cdot{10}^{-19}\ kg/m^3$

b) Pelo teorema do impulso, temos:

$\dpi{100} \large \vec{I}=\Delta \vec{Q}$

$\dpi{100} \large \vec{F}\cdot\Delta t=m\cdot \Delta \vec{v}$

$\dpi{100} \large \vec{F}=\frac{m\cdot \Delta \vec{v}}{\Delta t}$

Devemos assumir que a massa da poeira é desprezível frente à massa da Terra. Além disso, devemos assumir que a velocidade inicial da poeira também é desprezível. Substituindo a massa da Terra:

$\dpi{100} \large F=\frac{1000\cdot30\cdot{10}^3}{20\cdot60}=\frac{30\cdot{10}^6}{12\cdot{10}^2}=2,5\cdot{10}^4\ N=2,5\ kN$

Questão 12 da prova de Física Unicamp

Um densímetro de posto de combustível, usado para analisar o etanol, consiste de um tubo de vidro que fica parcialmente submerso no etanol. O peso do tubo é fixo, de forma que o volume do tubo que fica submerso depende da densidade do etanol. Uma escala na parte superior do tubo indica o valor da densidade medida.

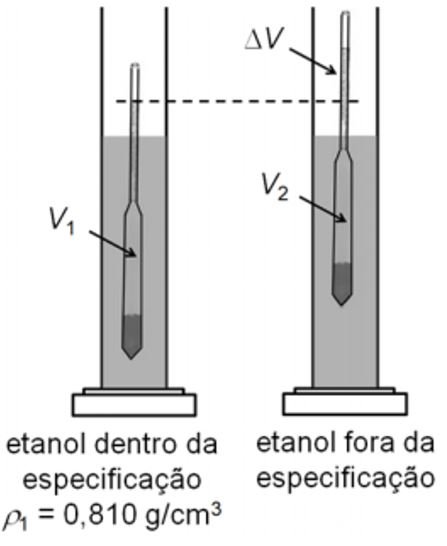
a) O etanol combustível é hidratado, ou seja, contém uma porcentagem de água. A figura ao lado ilustra duas medidas de densidade de etanol. A primeira é de uma amostra de etanol hidratado dentro da especificação, cujo valor é $\dpi{100} \large \rho_1=0,810\ g/cm^3$ . Nessa medida, o volume submerso do densímetro é $\dpi{100} \large V_1$ . A segunda medida, realizada com o mesmo densímetro, é de uma amostra fora da especificação e, nesse caso, o volume submerso do densímetro é $\dpi{100} \large V_2$ . A diferença dos volumes submersos é de 10% de $\dpi{100} \large V_1$ , ou seja, $\dpi{100} \large \Delta V=V_1-V_2=0,1\ V_1$ . Qual é a densidade $\dpi{100} \large \rho_2$ da segunda amostra?

b) Num posto de combustível, a gasolina é bombeada do reservatório subterrâneo até o tanque do veículo, numa altura $\dpi{100} \large h=3,0\ m$ acima do nível superior do reservatório. A gasolina, que é sempre retirada da parte superior do reservatório, encontra-se inicialmente parada e é despejada no tanque do veículo a uma velocidade $\dpi{100} \large v=0,8\ m/s$ .

Dado: $\dpi{100} \large \rho_{gasolina}=0,75\ g/cm^3$ .

Comentários

a) Nas duas situações, temos o equilíbrio entre a força peso do densímetro e o empuxo exercido pelo etanol.

$\dpi{100} \large \left\{\begin{matrix}\vec{P}={\vec{E}}_1\\\vec{P}={\vec{E}}_2\\\end{matrix}\right.$

Como o peso do densímetro não se altera, podemos escrever:

$\dpi{100} \large E_1=E_2$

$\dpi{100} \large \rho_1\cdot V_1\cdot g=\rho_2\cdot V_2\cdot g$

$\dpi{100} \large \rho_1\cdot V_1\cdot\cancel g=\rho_2\cdot V_2\cdot\cancel g$

$\dpi{100} \large \rho_1\cdot V_1=\rho_2\cdot V_2$

Pela relação entre os volumes fornecidas no enunciado, temos:

$\dpi{100} \large V_1-V_2=0,1V_1$

$\dpi{100} \large -V_2=0,1V_1-V_1$

$\dpi{100} \large V_2=V_1-0,1V_1=0,9V_1$

Voltando para a expressão anterior:

$\dpi{100} \large \rho_1\cdot V_1=\rho_2\cdot V_2$

$\dpi{100} \large \rho_1\cdot V_1=\rho_2\cdot0,9V_1$

$\dpi{100} \large \rho_1\cdot\cancel{V_1}=\rho_2\cdot0,9\cdot\cancel{V_1}$

$\dpi{100} \large \rho_1=\rho_2\cdot0,9\Rightarrow\rho_2=\frac{\rho_1}{0,9}$

$\dpi{100} \large \rho_2=\frac{0,810}{0,9}=0,900\ g/cm^3$

b) A variação da energia mecânica será dada pela soma da variação da energia cinética e da energia potencial gravitacional adquirida pela gasolina. Perceba que devemos desprezar a variação da altura do fluido no tanque, visto que o volume retirado é desprezível frente ao total nele armazenado.

$\dpi{100} \large \Delta E_{mec}=\Delta E_{cinetica}+\Delta E_{pot\ gravitacional}$

$\dpi{100} \large \Delta E_{mec}=\frac{m_{total}\cdot v^{2}}{2}+m_{total}\cdot g\cdot \Delta h$

A massa da gasolina pode ser calculada pelo produto entre o volume bombeado e a sua massa específica:

$\dpi{100} \large d_{gas}=\frac{m_{gas}}{V_{gas}}\Rightarrow m_{gasolina}=d_{gas}\cdot V_{gas}$

Note que $\dpi{100} \large V=40\ l=40\ dm^3=40\cdot{10}^3\ cm^3$ :

$\dpi{100} \large m_{gasolina}=0,75\cdot40\cdot{10}^3=30\cdot{10}^3g=30\ kg$

Voltando à expressão anterior:

$\dpi{100} \large \Delta E_{mec}=\frac{30\cdot\left(0,8\right)^2}{2}+30\cdot10\cdot3,0$

$\dpi{100} \large \Delta E_{mec}=9,6+900=909,6\ J$

Questão 13

Relês são dispositivos eletromecânicos usados para abrir e fechar contatos elétricos através da deflexão de uma lâmina metálica (armadura) que é atraída pelo campo magnético gerado por uma bobina, conforme ilustra a Figura A.

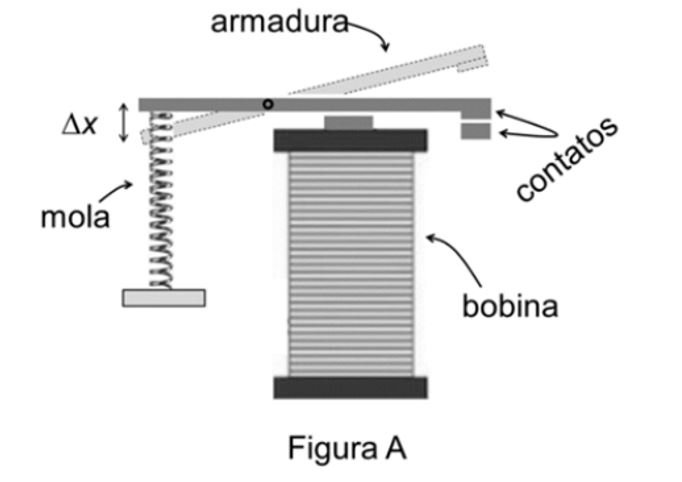
a) No relê da Figura A, a constante elástica da mola presa à armadura é $\dpi{100} \large k=1500\ N/m$ . Quando a bobina é ligada, qual é a energia potencial da mola, se ela for distendida de ∆x=0,8 mm em relação à sua posição de equilíbrio?

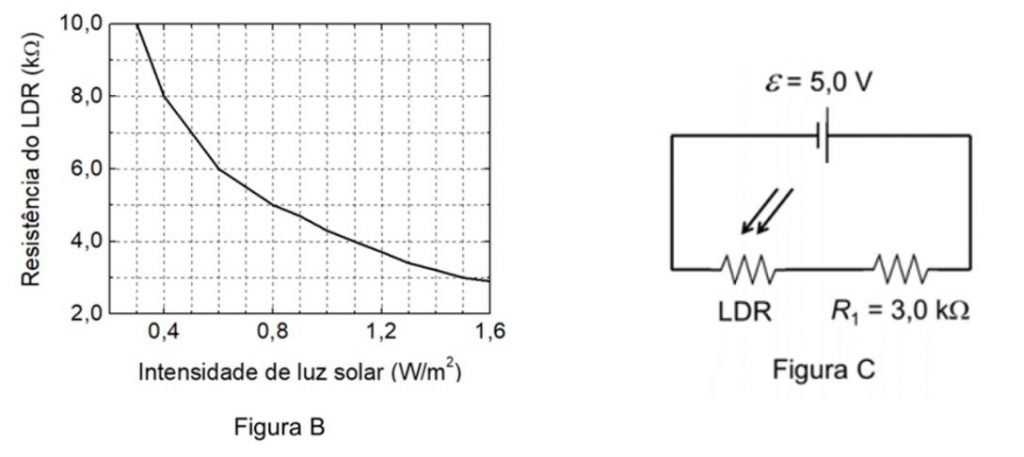
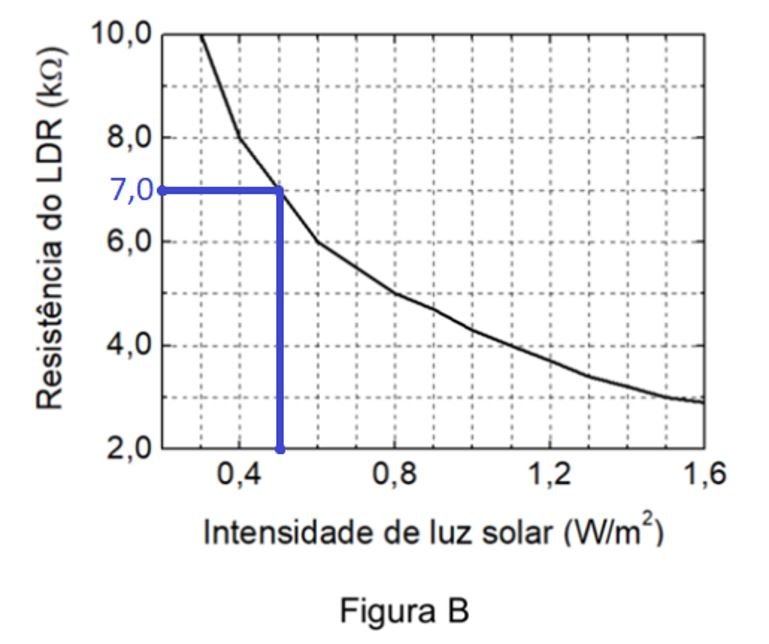
b) Resistores LDR (Resistor Dependente de Luz) apresentam alta resistência elétrica na ausência de luz, e baixa resistência quando iluminados. Um uso frequente desses resistores se verifica no acionamento de relês. A Figura B (no espaço de resposta) fornece a resistência do LDR do circuito da Figura C em função da intensidade luminosa. Qual é a tensão no LDR quando a intensidade de luz solar nele incidente é igual a $\dpi{100} \large I=0,5\ W/m^2\$ ?

Comentários

a) A energia potencial da mola pode ser calculada por:

$\dpi{100} \large E_{el}=\frac{k\cdot\left(\Delta x\right)^2}{2}$

$\dpi{100} \large E_{el}=\frac{1500\cdot\left(0,8\cdot{10}^{-3}\right)^2}{2}=\frac{1,5\cdot{10}^3\cdot0,64\cdot{10}^{-6}}{2}$

$\dpi{100} \large E_{el}=0,48\cdot{10}^{-3}=4,8\cdot{10}^{-4}\ J$

b) Pelo gráfico, devemos extrair a resistência do LDR dada a intensidade de luz solar $\dpi{100} \large I=0,5\ W/m^2$ :

Sendo $\dpi{100} \large R_{LDR}=7,0\cdot{10}^3\ \Omega$ , podemos usar a primeira lei de Ohm para determinarmos a corrente do circuito. Note que os dois resistores estão ligados em série, assim a resistência equivalente é dada pela soma dos dois:

$\dpi{100} \large R_{eq}=R_1+R_{LDR}=3,0\cdot{10}^3+7,0\cdot{10}^3=10\cdot{10}^3\Omega$

Aplicando a primeira lei:

$\dpi{100} \large \varepsilon=R_{eq}\cdot i\Rightarrow i=\frac{\varepsilon}{R_{eq}}=\frac{5}{10\cdot{10}^3\ }=0,5\cdot{10}^{-3}A=0,5\ mA$

A tensão no LDR pode ser calculada de maneira similar:

$\dpi{100} \large V_{LDR}=R_{LDR}\cdot i$

$\dpi{100} \large V_{LDR}=7,0\cdot{10}^3\cdot0,5\cdot{10}^{-3}=3,5\ V$

Questão 14 da prova de Física Unicamp

Filtros ópticos têm muitas aplicações: óculos de sol, equipamentos fotográficos, equipamentos de proteção individual (EPI) em atividades profissionais, etc. A densidade óptica de um filtro (OD) é definida por $\dpi{100} \large OD=-\log_{10}{T}$ , sendo T a transmitância óptica, que é dada pela razão entre a intensidade luminosa transmitida e a intensidade incidente. Nas máscaras de soldador, bem como naquelas usadas para a observação direta do Sol durante um eclipse, são necessários filtros de densidades ópticas muito elevadas, ou seja, filtros que transmitem muito pouca luz, tanto na região visível (de 400 nm a 700 nm) quanto no ultravioleta e no infravermelho.

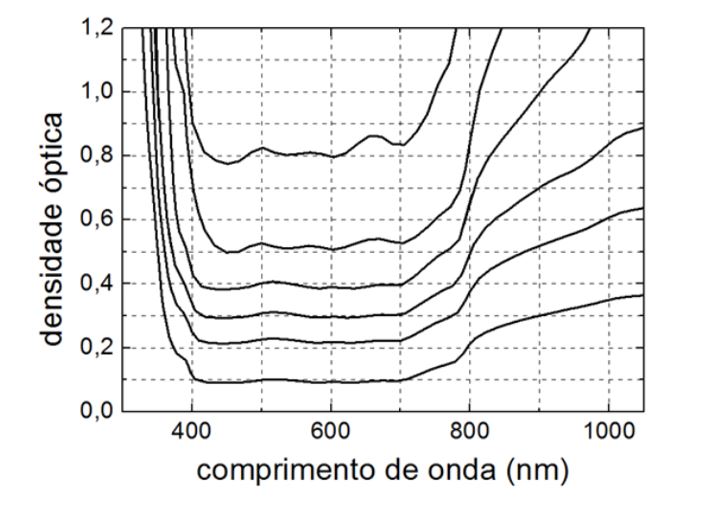
a) No espaço de resposta, apresenta-se um gráfico da densidade óptica em função do comprimento de onda $\dpi{100} \large \lambda$ para vários filtros, sendo que para cada um deles a densidade óptica na região visível é aproximadamente constante. Quanto vale a transmitância para $\dpi{100} \large \lambda=900\ nm$ do filtro de $\dpi{100} \large OD\ \sim \ 0,4$ na região visível?

b) A água é um bom filtro óptico no infravermelho próximo, e tem um pico de absorção em comprimentos de onda ligeiramente inferiores a $\dpi{100} \large 3,0\ \mu m$ . A energia do fóton é dada por $\dpi{100} \large E=hf$ , em que $\dpi{100} \large h=6,6\cdot{10}^{-34}\ J\cdot s$ é a constante de Planck, e f é a frequência da onda eletromagnética. Quanto vale a energia do fóton absorvido no comprimento de onda $\dpi{100} \large \lambda=3,0\ \mu m$ ?

*A velocidade da luz no vácuo vale $\dpi{100} \large c=3,0\cdot{10}^8\ m/s$ .

Comentários

a) Pelo gráfico, se o filtro possui $\dpi{100} \large OD\cong4$ , na região do visível, sabemos se tratar da terceira curva de cima para baixo. Podemos usar o mesmo gráfico para determinarmos a densidade óptica para o comprimento de onda $\dpi{100} \large \lambda=900\ nm$ :

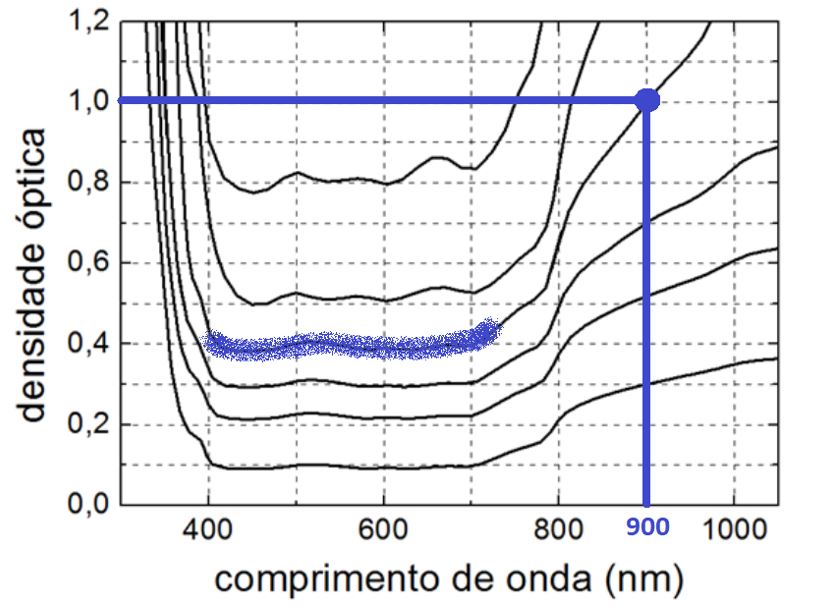
Sabendo que OD=1, podemos calcular a transmitância óptica:

$\dpi{100} \large OD=-\log_{10}{T}$

$\dpi{100} \large \log_{10}{T}=-OD$

$\dpi{100} \large T={10}^{-OD}={10}^{-1}=0,1$

b) A energia do fóton, como dito no enunciado, é calculada por:

$\dpi{100} \large E=h\cdot f$

Podemos escrever a frequência em função da velocidade e do comprimento de onda, fazendo uso da equação fundamental da ondulatória:

$\dpi{100} \large v=\lambda\cdot f\Rightarrow f=\frac{v}{\lambda}$

Voltando à expressão da energia do fóton:

$\dpi{100} \large E=h\cdot f=h\cdot\frac{v}{\lambda}$

$\dpi{100} \large E=6,6\cdot{10}^{-34}\cdot\frac{3,0\cdot{10}^8}{3,0\cdot{10}^{-6}}=6,6\cdot{10}^{-34}\cdot\frac{\cancel{3,0}\cdot{10}^8}{\cancel{3,0}\cdot{10}^{-6}}$

$\dpi{100} \large E=6,6\cdot{10}^{-34}\cdot1\cdot{10}^{14}=6,6\cdot{10}^{-20}\ J$

Questão 15

As vidraças de um arranha-céu em Londres, conhecido como “Walkie Talkie”, reproduzem a forma de um espelho côncavo. Os raios solares refletidos pelo edifício provocaram danos em veículos e comércios próximos.

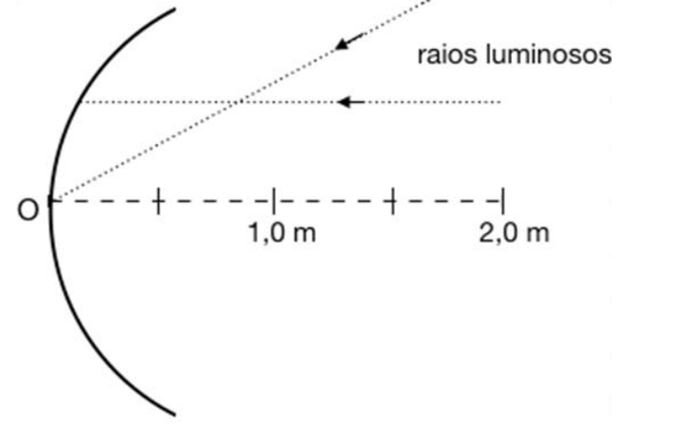
a) Considere um objeto em frente e ao longo do eixo do espelho côncavo de raio de curvatura R=1,0 m, conforme mostra a figura no espaço de resposta. Complete os raios luminosos na figura. Em seguida, calcule a distância d do objeto ao vértice do espelho (ponto O), de forma que a intensidade de raios solares, incidentes paralelamente ao eixo do espelho, seja máxima na posição do objeto.

b) Um objeto metálico de massa m=200 g e calor específico $\dpi{100} \large c=480\ J\left(kg\cdot\ \degree C\right)$ absorve uma potência P=60 W de radiação solar focalizada por um espelho côncavo. Desprezando as perdas de calor por radiação, condução e convecção, calcule a variação de temperatura do objeto após ∆t=32 s de exposição a essa radiação.

Comentários

a) Devemos nos lembrar das propriedades dos raios que chegam até um espelho esférico. Raios paralelos ao eixo principal devem ser refletidos em direção ao foco do espelho e raios que incidem no vértice são refletidos com mesmo ângulo de incidência:

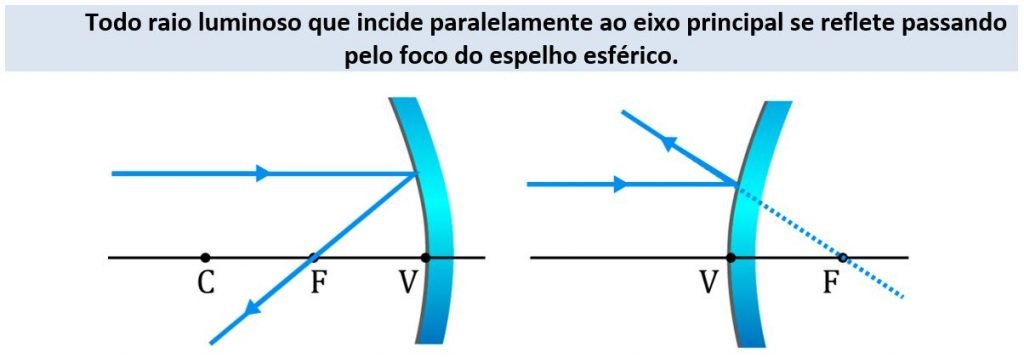
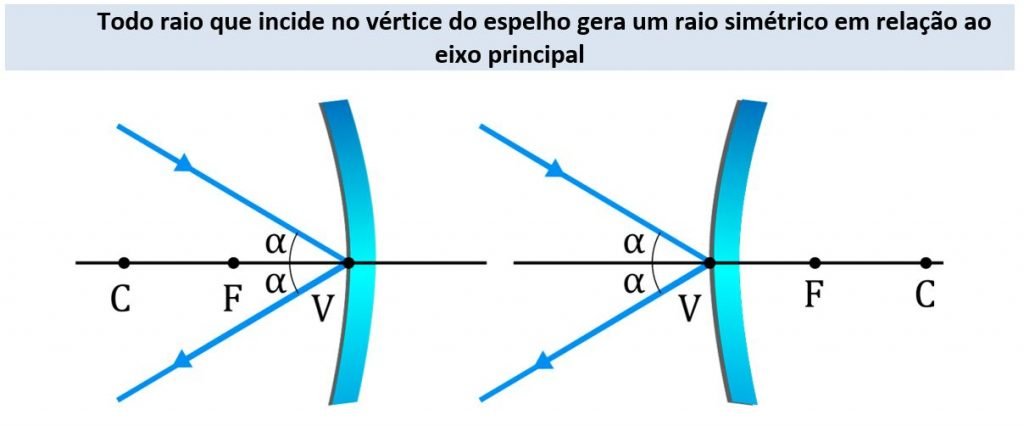
Para a questão:

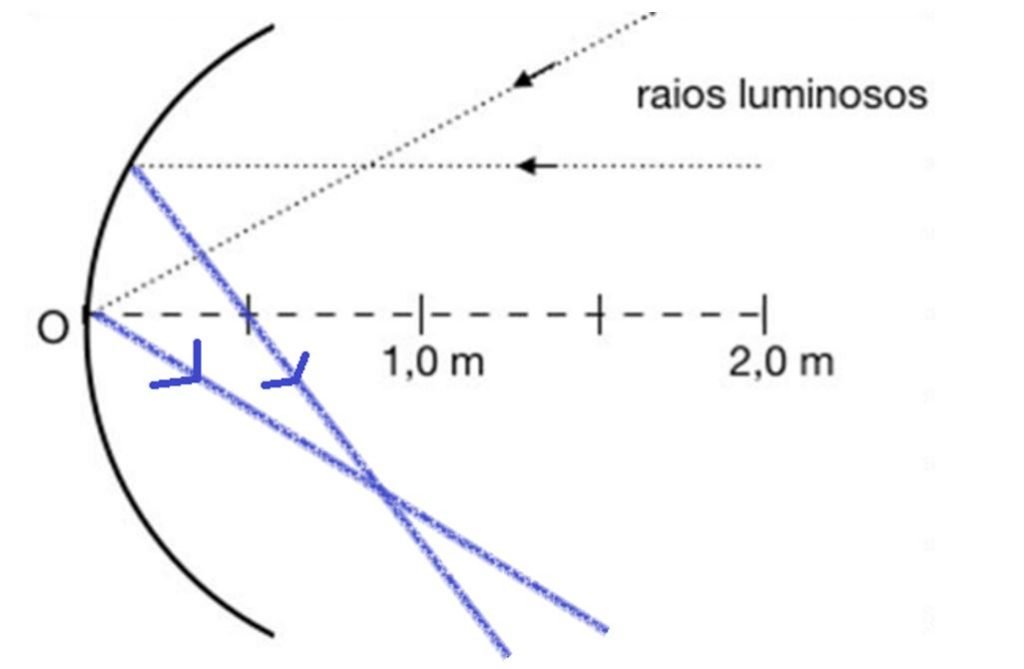
Os raios paralelos convergem para o foco. Dessa forma, para que a intensidade dos raios seja máxima, o objeto deve estar posicionado a uma distância de 0,5 m do vértice do espelho, que corresponde à metade do seu raio.

b) Devemos usar a definição da potência, em conjunto com a equação fundamental da calorimetria:

$\dpi{100} \large Pot=\frac{E}{\Delta t}$

$\dpi{100} \large Pot=\frac{m\cdot c\cdot\Delta \theta}{\Delta t}$

Podemos isolar o tempo e substituir os valores fornecidos:

$\dpi{100} \large \Delta \theta=\frac{Pot\cdot \Delta t}{m\cdot c}=\frac{60\cdot32}{200\cdot{10}^{-3}\cdot480\ \ }=\frac{60\cdot32}{2\cdot{10}^{-1}\cdot4,8\cdot{10}^2\ }$

$\dpi{100} \large \Delta \theta=\frac{1920}{2\cdot{10}^{-1}\cdot4,8\cdot{10}^2\ }=\frac{1920}{96}=20\ °C$

Questão 16 da prova de Física Unicamp

Julho de 2019 marcou o cinquentenário da chegada do homem à Lua com a missão Apollo 11. As caminhadas dos astronautas em solo lunar, com seus demorados saltos, são imagens emblemáticas dessa aventura humana.

a) A aceleração da gravidade na superfície da Lua é $\dpi{100} \large g_L=1,6\ m/s^2$ . Calcule o tempo de queda de um corpo solto a partir do repouso de uma altura de 1,8 m com relação à superfície lunar.

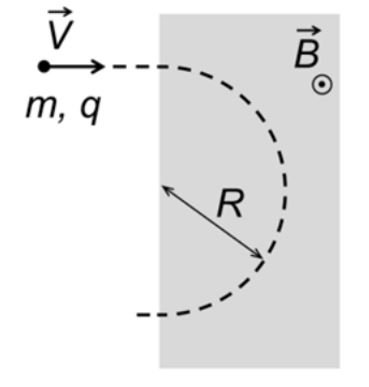
b) A espectrometria de massas é uma técnica que pode ser usada na identificação de moléculas da atmosfera e do solo lunar. A figura ao lado mostra a trajetória (no plano do papel) de uma determinada molécula ionizada (carga $\dpi{100} \large q=1,6\cdot{10}^{-19}C$ ) que entra na região de campo magnético do espectrômetro, sombreada na figura, com velocidade de módulo $\dpi{100} \large V=3,2\cdot{10}^5m/s$ . O campo magnético é uniforme e perpendicular ao plano do papel, dirigido de baixo para cima, e tem módulo B=0,4T. Como ilustra a figura, na região de campo magnético a trajetória é circular de raio R=36 cm, e a força centrípeta é dada pela força magnética de Lorentz, cujo módulo vale F=qVB. Qual é a massa m da molécula?

Comentários

a) Podemos usar a equação da posição em função do tempo para determinarmos o tempo de queda. Sabemos que a velocidade inicial é nula, e que a aceleração da gravidade age a favor durante a queda:

$\dpi{100} \large \Delta S=v_0\cdot t+\frac{a\cdot t^2}{2}$

$\dpi{100} \large \Delta S=\cancel{v_0}\cdot t+\frac{a\cdot t^2}{2}$

$\dpi{100} \large \Delta S=\frac{a\cdot t^2}{2}\Rightarrow t^2=\frac{2\cdot \Delta S}{a}$

$\dpi{100} \large t=\sqrt{\frac{2\cdot \Delta S}{a}}=\sqrt{\frac{2\cdot1,8}{1,6}}=\sqrt{\frac{3,6}{1,6}}=\sqrt{\frac{36}{16}}=\frac{6}{4}=1,5\ s$

b) Sabemos que a força magnética atua como resultante centrípeta. Desse modo, podemos igualar as duas relações e isolar a massa:

$\dpi{100} \large F_{cp}=F_{mag}$

$\dpi{100} \large \frac{m\cdot v^2}{R}=q\cdot v\cdot B$

$\dpi{100} \large \frac{m\cdot v^{\cancel{2}}}{R}=q\cdot\cancel{v}\cdot B$

$\dpi{100} \large \frac{m\cdot v}{R}=q\cdot B$

$\dpi{100} \large m=\frac{q\cdot B\cdot R}{v}$

$\dpi{100} \large m=\frac{1,6\cdot{10}^{-19}\cdot0,4\cdot36\cdot{10}^{-2}}{3,2\cdot{10}^5}$

$\dpi{100} \large m=\frac{{10}^{-21}\cdot0,4\cdot36}{2\cdot{10}^5}=7,2\cdot{10}^{-26}\ kg$

Com isso, encerramos a nossa correção da prova de Física Unicamp 2ª Fase 2020. Se ficou alguma dúvida, pode entrar em contato comigo através do nosso Fórum de Dúvidas ou pelas minhas redes sociais. Vou deitar esta correção disponível para download. Você vai poder baixar de forma gratuita no link a seguir.

">Resolução Física UNICAMP 2020 – 2ª Fase" class="wp-block-file__button" download>Baixar

Abraços

Prof. Lucas Costa

Instagram: @prof.lucascosta

Resolução da prova de Física Unicamp 2ª Fase 2020

Questão 11

Questão 12 da prova de Física Unicamp

Comentários

Questão 13

Comentários

Questão 14 da prova de Física Unicamp

Comentários

Questão 15

Comentários

Questão 16 da prova de Física Unicamp

Comentários

Veja também:

Raquel Oshio

Confira o gabarito da prova de Biologia da Unicamp, 2ª Fase

Comentários sobre a prova de História da 2ª Fase da Unicamp

Movimento Circular Uniforme e Uniformemente Variado (MCU e MCUV): o que são, fórmulas e exemplos

Lançamento oblíquo: conceito, fórmulas e questões

Leis de Kepler: quais são, conceitos e fórmulas

Resolução da prova de Física Unicamp 2ª Fase 2020

Questão 11

Questão 12 da prova de Física Unicamp

Comentários

Questão 13

Comentários

Questão 14 da prova de Física Unicamp

Comentários

Questão 15

Comentários

Questão 16 da prova de Física Unicamp

Comentários

Veja também:

Raquel Oshio

Confira o gabarito da prova de Biologia da Unicamp, 2ª Fase

Comentários sobre a prova de História da 2ª Fase da Unicamp

Você pode gostar também