Você já deve ter se deparado com as palavras círculo e circunferência como sinônimos no dia a dia. Acontece que, matematicamente, os conceitos que esses termos representam não são os mesmos.
No artigo a seguir, você verá um panorama e diferenciação entre as duas definições. Além disso, confira como eles aparecem nos vestibulares, com exercícios e resoluções. Leia agora!
Navegue pelo conteúdo
O que é circunferência?
A circunferência é um conjunto de pontos que possuem a mesma distância de um ponto principal. Por exemplo, se imaginarmos um ponto E qualquer e definirmos r como um raio, pode-se dizer que todos os pontos V que estão a r centímetros de E fazem parte da circunferência.
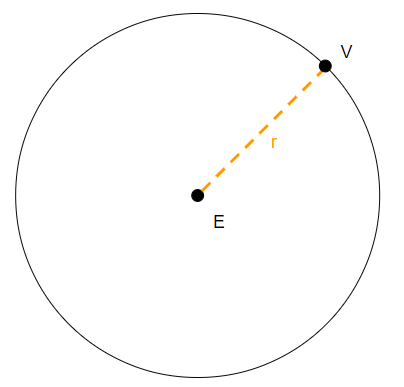
Veja que interessante: embora a formação circunferencial esteja centrada no ponto central E, ele não faz parte da circunferência — ela está limitada aos diversos pontos que formam a “roda”, mas o seu centro não está incluso na definição. Curioso, não?!
Circunferência na geometria plana
Na geometria plana, conhecer o comprimento de uma circunferência pode ser determinante para situações do dia-a-dia, veja: quando mede-se a circunferência de um pneu, entende-se quantos centímetros a roda anda em cada volta completa.
Na planificação, a medida pode ser ilustrada como traçar o contorno circunferencial com um pedaço de barbante, depois abrí-lo e medir seu comprimento. Com os estudos matemáticos, entendeu-se que esse processo seria equivalente a realizar o cálculo:
Circunferência = C = 2.?.r
Além disso, é importante saber que geometria plana considera que o segmento de reta que cruza o centro da circunferência é chamado de diâmetro e mede exatamente o valor de dois raios: diâmetro = 2.r
Na questão abaixo, que apareceu na prova do Enem em 2014, esses conceitos são explorados, acompanhe a resolução!
Uma empresa que organiza eventos de formatura confecciona canudos de diplomas a partir de folhas de papel quadradas. Para que todos os canudos fiquem idênticos, cada folha é enrolada em torno de um cilindro de madeira de diâmetro d em centímetros, sem folga, dando-se 5 voltas completas em torno de tal cilindro. Ao final, amarra-se um cordão no meio do diploma, bem ajustado, para que não ocorra o desenrolamento, como ilustrado na figura:
Em seguida, retira-se o cilindro de madeira do meio do papel enrolado, finalizando a confecção do diploma. Considere que a espessura da folha de papel original seja desprezível.
Qual é a medida, em centímetros, do lado da folha de papel usado na confecção do diploma?
a) π d
b) 2π d
c) 4π d
d) 5π d
e) 10π d
Primeiro, precisamos ter em mente que a fórmula da circunferência é C = 2.?.r = 2.r.? e que o diâmetro d=2.r. Portanto, podemos explorar os cálculos com:
C = d.?
Depois, é necessário observar que o papel, para dar exatas 5 voltas em torno do cilindro, deve possuir 5 vezes a circunferência desse sólido geométrico, assim:
Comprimento do papel = 5.C
Comprimento do papel = 5.d.? , conforme alternativa D.
Circunferência na geometria analítica
Nas notações algébricas, pode-se dizer que: seja V um ponto genérico da circunferência e E o seu centro:
distância entre E e V = dEV = r
Considera-se que a distância entre dois pontos, na geometria analítica, é dada pela fórmula:
dAB² = (xB – xA)² + (yB – yA)²
Podemos manipular os dois sistemas e conseguir uma fórmula analítica para a circunferência:
d2EV = r2
r2 = (xE – xV)² + (yE – yV)²
Em termos genéricos, uma circunferência de centro C (a,b) obedecerá a regra:
(a – x)2 + (b – y)2 = r2
O que é círculo?
Agora que você já conhece a definição de circunferência, podemos partir para o conceito de círculo. Ele é composto pelos pontos que determinam a circunferência e, adicionalmente, também contém os pontos internos que estão delimitados por aquela linha.
Ou seja, o círculo é toda a área interna de uma circunferência. No cotidiano, ele aparece de diferentes formas: é a base do cilindro e do cone, compõe logotipos, faz parte da alfabetização infantil, entre outros exemplos.
Círculo na geometria plana
Na geometria plana, a principal característica do círculo é a área, que será dada com base no número irracional pi e no raio da circunferência, como demonstra a fórmula a seguir:
Acírculo = ? . r2
No vestibular da UNEMAT, caiu uma questão sobre a área do círculo, siga o desenvolvimento do raciocínio:
UNEMAT 2012
Se o raio de um círculo aumenta 20%, então a sua área aumentará
a) 0%.
b) 10%.
c) 20%.
d) 40%.
e) 44%.
Vamos considerar que a área inicial do círculo seja A = ? . r2.
A partir disso, aumentamos em 20% do valor do raio, que passará a ser 1,2.r, ou seja:
A’= ? . (1,2.r)2
Com isso, realizam-se os novos cálculos e percebe-se que:
A’= ? . 1,44. r2
Nota-se, então que, A’ = 1,44.A. De forma que houve um aumento de 44% na área total do círculo, como aponta a alternativa E.
+ Veja também: Como calcular porcentagem?
Círculo na geometria analítica
Na geometria analítica, por sua vez, as inequações são utilizadas para determinar os pontos que estão inclusos no formato circular e aqueles que não se inserem na figura. Veja:
- Quando um ponto possui distância do centro maior do que o valor do raio, ele está fora da delimitação circunferencial e não faz parte do círculo; ou
- Se um ponto está distante do centro em uma medida menor do que o raio, então ele está incluso no círculo determinado pela circunferência genérica C.
Em termos algébricos, para que um ponto esteja presente no círculo, deve obedecer a seguinte equação:
dEV ≤ r
√[(a – x)2 + (b – y)2] ≤ r
(a – x)2 + (b – y)2 ≤ r2
Para um dado círculo de centro E (a,b) e um ponto genérico V(x,y).
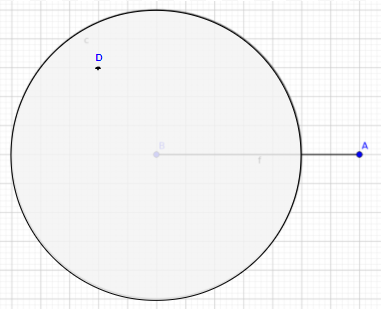
Observe, na imagem abaixo, que o ponto A tem uma distância do centro muito maior que o valor do raio, por isso ele não se enquadraria na inequação (a – x)2 + (b – y)2 ≤ r2.
Por outro lado, o ponto D, como está representado, encontra-se em uma distância do centro menor do que o raio e, portanto, se encaixa nas definições algébricas e gráficas da inequação.
+ Veja também: Geometria Espacial: conheça os sólidos e fórmulas
Quer aprender mais de círculo e circunferência?
Você precisa encontrar mais informações sobre geometria plana e analítica? Acompanhe o canal do Estratégia Vestibulares: diversas aulas gratuitas e didáticas são disponibilizadas frequentemente na plataforma, você não vai se arrepender!
Conheça também o Curso Preparatório para o Enem: com ele você tem acesso aulas em vídeo, um vasto material em PDF e a milhares de questões de vestibulares, com resolução comentada e classificação por provas. Clique no banner abaixo e aprimore seus estudos!
Veja também:
- Geometria: o que é e como é classificada
- Figuras Geométricas: planas, espaciais e como aparece nos vestibulares
- Geometria Plana no Enem: conceito e definições
- Triângulos: definição, perímetro, área, classificações
- Semelhança de triângulos
- Geometria analítica: fórmulas, gráficos e equações
- Geometria Espacial: conheça os sólidos e fórmulas
- Área do trapézio: conheça a fórmula e como calcular!
- Prova FUVEST 2020 – Matemática – Resolução Comentada
- Resolução da prova de Matemática da 2ª Fase da Unicamp 2020
- Prova UNESP 2020 – Matemática – Resolução Comentada




