A trigonometria é uma importante área da Matemática que costuma cair sempre nas provas do Enem e de diversos vestibulares do país, como Fuvest e Unicamp. Então, não perca esse conteúdo que o Estratégia Vestibulares preparou para você gabaritar as questões de trigonometria e garantir a sua vaga na universidade.
Navegue pelo conteúdo
O que é trigonometria?
A trigonometria é um ramo da Matemática que estuda os triângulos e os ângulos presentes nele.
Círculo trigonométrico
O círculo trigonométrico é uma ferramenta utilizada para visualizar os ângulos e seus respectivos quadrantes.
No círculo, os ângulos são dispostos de 0 a 360º, – totalizando uma volta completa – e dividido entre quatro quadrantes, como você pode observar na figura abaixo:
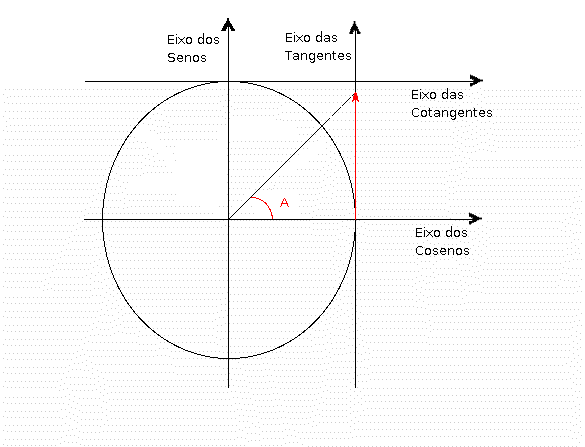
Um fato relevante sobre o círculo trigonométrico é que cada um dos quatro quadrantes – numerados de I a IV na imagem – possui um ângulo de 90º, visto que representam um quarto da volta completa do círculo.
Além disso, é importante lembrar que os ângulos crescem de maneira anti – horária e que o eixo vertical simboliza os valores do seno e o eixo horizontal, os valores do cosseno, sendo que esse círculo possui o valor do raio igual a um.
Triângulo retângulo
O triângulo retângulo é uma forma geométrica fundamental para a trigonometria porque, a partir dele, é possível montar diversas relações importantes para os cálculos.
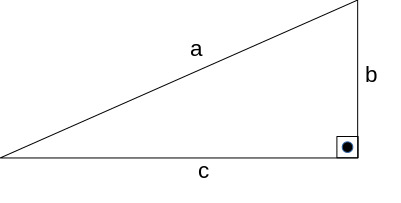
Veja os elementos presentes no triângulo retângulo:
- Ângulo reto: indicado por um quadrado que está sempre entre os catetos e de frente para a hipotenusa. Esse ângulo mede 90º e um triângulo só pode ser retângulo se possuir um ângulo reto;
- Catetos: são os lados do triângulo que ficam adjacentes ao ângulo reto e são representados pelas letras “b” e “c” na figura abaixo; e
- Hipotenusa: é o maior lado do triângulo retângulo e é o lado que fica “em frente” ao ângulo reto, sem que haja o contato entre eles. A hipotenusa está representada pela letra “a” no desenho.
Trigonometria no triângulo retângulo
A partir do triângulo retângulo é possível entender alguns conceitos muito utilizados na área da trigonometria como o conceito de seno, de cosseno e de tangente, além de encontrar os seus valores. Observe os ângulos ∝ e β na figura a seguir:
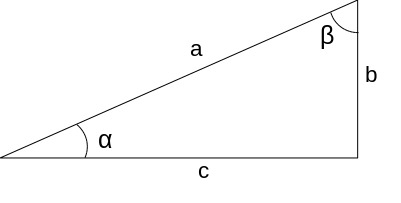
Perceba que os lados “b” e “c” permanecem como catetos e o lado “a” continua sendo a hipotenusa nesse exemplo. Contudo, o título de “oposto” ou de “adjacente” é atribuído aos catetos de acordo com o ângulo que esteja sendo observado.
Logo, para o ângulo ∝, o cateto oposto a ele é o lado “c” e o cateto adjacente a ele é o lado “b”. Enquanto, para o ângulo β, o cateto oposto a ele é o lado “b” e o cateto adjacente é o lado “c”.
Agora que você já sabe como identificar os catetos, vamos ver as relações entre eles:
- Seno: é a razão entre o cateto oposto ao ângulo observado e a hipotenusa do triângulo, e pode ser descrito pela seguinte fórmula:
sen = cateto oposto / hipotenusa
- Cosseno: é a razão entre o cateto adjacente ao ângulo observado e a hipotenusa do triângulo, e pode ser descrita pela seguinte fórmula:
cos = cateto adjacente / hipotenusa
- Tangente: é a razão entre o cateto oposto e o cateto adjacente ao ângulo observado, e pode ser descrita pela seguinte fórmula:
tg = cateto oposto / cateto adjacente
Além disso, por meio da manipulação de fórmulas, é possível perceber que a tangente pode ser representada como a razão entre o seno e o cosseno do ângulo que está sendo trabalhado. Veja essa razão a seguir:
tg = sen / cos
Sendo um ângulo qualquer, utilizado apenas como exemplo.
Achou muita fórmula? Não se preocupe! A Coruja tem um macete para te ajudar a memorizar:
SOH CAH TOA
Em que S simboliza o seno, O simboliza o cateto oposto, H é a hipotenusa, C é o cosseno e T representa a tangente! Assim, você vai lembrar quais são os elementos do triângulo retângulo utilizados no cálculo de cada medida.
Funções da trigonometria
As duas principais funções da trigonometria são a função seno, definida por f(x) = sen(x), que apresenta um gráfico em forma de senoide, e a função cosseno, definida por f(x) = cos(x), a qual possui um gráfico em forma de uma cossenoide.
Teorema de Pitágoras
O Teorema de Pitágoras é baseado no triângulo retângulo e afirma que o quadrado da hipotenusa do triângulo é igual a soma dos quadrados dos catetos.
Portanto, esse teorema pode ser descrito como:
a² = b² + c²
Lei dos senos
Para um triângulo qualquer, a lei dos senos vale:
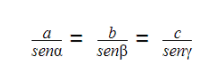
Sendo “a” o lado em frente ao ângulo , “b” o lado em frente ao ângulo , e “c”, o lado em frente ao ângulo .
Lei dos cossenos
A lei dos cossenos possui três formas possíveis, uma para cada lado do triângulo. Veja abaixo:
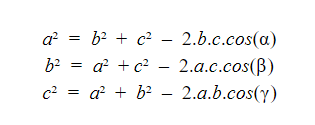
Lei das tangentes
A lei das tangentes é a relação entre dois ângulos e os lados que estão em sua frente:
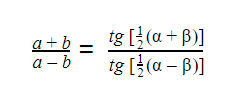
Exercício
Agora que você já tem um bom conhecimento sobre a trigonometria, resolva essa questão que o Estratégia Vestibulares preparou para você:
(FUVEST) Dois pontos A e B estão situados na margem de um rio e distantes 40 m um do outro. Um ponto C, na outra margem do rio, está situado de tal modo que o ângulo CÂB mede 75° e o ângulo ACB mede 75°. Determine a largura do rio.
- 40 m
- 20 m
- 20√3 m
- 30 m
- 25
Gabarito: B
Gostou do conteúdo que o Estratégia Vestibulares preparou para você ir bem na prova de Matemática do Enem e do seu vestibular? Então não perca nossos próximos artigos! Aproveite para conhecer os nossos cursos, que são pensados para você alcançar seu sonho de entrar na universidade. Clique no banner abaixo e confira!
Veja também:
- Círculo trigonométrico: o que é, exemplos, usos e aplicações
- Aproximação sen(x) = tg(x) = xe suas aplicações no vestibular
- Seno, cosseno e tangente: como calcular, tabela e formulas
- Prova de matemática Fuvest 2020 com Resolução Comentada
- Resolução da prova de Matemática da 2ª Fase da Unicamp 2020
- Prova de Matemática UNESP 2020 com Resolução Comentada
- Operações com arcos: o que são, ciclo trigonométrico e como fazer
- Funções trigonométricas: fórmulas, gráficos e aplicações



