O lançamento oblíquo de um objeto acontece por exemplo, no arremesso de uma bola durante uma partida de vôlei. Espera-se que a bola alcance uma altura máxima e depois caia em um ponto estratégico da quadra, para garantir a pontuação do time.
Trata-se de um assunto importante na cinemática, porque abrange diferentes situações do cotidiano. Diante disso, muitos vestibulares cobram o assunto, especialmente em provas específicas para cursos de exatas.
Se você quer aprender este tema e garantir um conhecimento a mais sobre física, continue lendo este artigo. Será abordado o conceito de lançamento oblíquo, qual a trajetória que os objetos lançados descrevem no espaço, as fórmulas utilizadas no estudo matemático do tema e, ainda, veja uma questão de vestibular comentada sobre o assunto!
Navegue pelo conteúdo
O que é lançamento oblíquo?
O lançamento oblíquo ocorre quando o objeto é arremessado com uma angulação maior do que zero, em relação ao eixo horizontal, de forma que há dois vetores velocidade (horizontal e vertical) não nulos desde o início do movimento.
O exemplo mais clássico de lançamento oblíquo são os projéteis, artifícios militares que permitem o disparo de balas a partir do solo em um sentido diagonal. Note que o corpo viaja pelo espaço com velocidades tanto “para cima” como “para o lado”, o que permite um trajeto não retilíneo após o lançamento.
Como há dois componentes vetoriais para um deslocamento oblíquo, é necessário que o estudo seja decomposto em vetores verticais (y) e horizontais (x), de preferência em um plano cartesiano, para facilitar a atribuição de valores matemáticos para seu posicionamento no espaço, por exemplo.
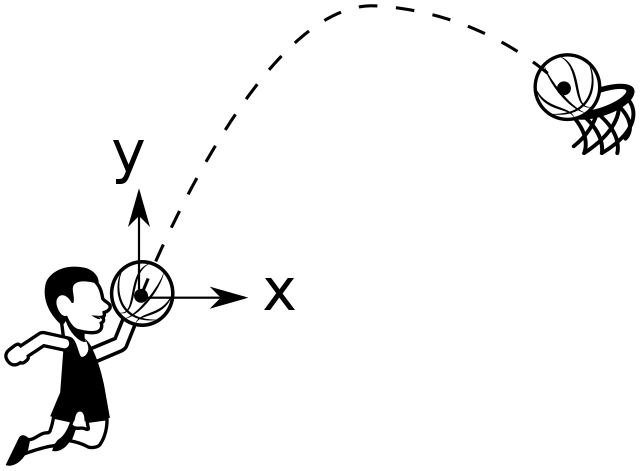
Se o movimento será descrito em dois eixos diferentes, então, as variáveis que atuam nele também podem ser estudadas dessa forma. Além disso, o deslocamento em x e y apresentará valores diferentes a depender da velocidade horizontal e vertical no início do lançamento oblíquo.
Fórmulas e gráficos de lançamento oblíquo
Eixo vertical
No eixo vertical, a partir do momento que um objeto é lançado no espaço de uma certa altura h (h≠0), haverá influência da aceleração da gravidade no movimento desse corpo. Diante disso, é possível determinar que a aceleração que atua em um material lançado obliquamente é constante, definição presente em um movimento uniformemente variado (MUV), com as fórmulas:
Para determinar a posição, velocidade de um corpo ou ainda o tempo transcorrido após um lançamento oblíquo, é possível utilizar as fórmulas do MUV:
V2 = V02+2gΔsy
ΔS = V0.t + g.t2/2
V = V0 + g.t
Δsy = V0.t + (a.t2)/2
- V = velocidade no ponto a ser estudado;
- V0 = velocidade inicial;
- g = aceleração da gravidade;
- t = tempo que está sendo observado, após o lançamento; e
- Δsy = diferença entre as posições inicial e final, no eixo vertical (deslocamento até o tempo estudado).
Nos estudos cinemáticos, é relevante adicionar um marco zero para indicar a posição inicial do corpo observado. Em geral, utiliza-se o ponto cartesiano (0,0) e depois são adicionados os pontos relativos ao seu posicionamento à medida que o tempo passa, em um gráfico tempo x altura, por exemplo. Quando esse tipo de descrição é realizada, observa-se que a trajetória do corpo desenha uma parábola no plano cartesiano.
Em matemática, o gráfico em formato de parábola indica que ele pode ser construído a partir de uma equação do segundo grau. Além disso, a parábola apresenta um ponto y vértice, que, no caso do lançamento oblíquo, indica a altura máxima (H) atingida por esse projétil ao longo do tempo de deslocamento, que pode ser encontrada a partir do cálculo:
H = (V02 . sen2 Ө)/2
- H = altura máxima atingida;
- Ө = ângulo de lançamento, em relação ao eixo horizontal;
- V0 = velocidade inicial no eixo vertical.
Quando o projétil é lançado obliquamente, sua velocidade vertical inicial terá intensidade diferente de zero e, à medida que ele sobe, será influenciado pela gravidade, diminuindo esse impulso de subida. Afinal, a velocidade aponta para cima e a gravidade tem um vetor em sentido contrário. Isso faz com que, na altura máxima da trajetória, a velocidade vertical do corpo seja nula.
Eixo horizontal
O eixo horizontal possui uma velocidade constante desde o início da trajetória, de forma que seu estudo gráfico revela um movimento retilíneo uniforme (MRU). Então, as fórmulas utilizadas para compreender o deslocamento horizontal do corpo estudado serão:
V = Δsx/ Δt
S (t) = S0 + V.t
- V = velocidade do movimento;
- Δt = intervalo de tempo entre início e momento estudado;
- S0 = posição inicial do corpo no eixo horizontal;
- t = momento em que o movimento está sendo estudado;
- S = posição do corpo no tempo em questão;
- Δsx = variação da posição desde o início até o tempo em questão.
O objeto lançado obliquamente possui um alcance horizontal máximo (A) ao longo de sua trajetória, que representa a distância retilínea entre o ponto de lançamento e o ponto em que ele para seu deslocamento.
A = V.cos Ө.t
- A = alcance máximo;
- Ө = ângulo entre o eixo horizontal e o eixo de lançamento;
- t = momento estudado.
+ Veja também: Cálculo vetorial: o que é, como fazer e aplicações
Questão sobre lançamento oblíquo
Universidade Estadual do Ceará (UECE) – 2020
Considere uma bola de futebol que, após o chute, descreve uma trajetória parabólica em relação à superfície horizontal de lançamento. Desprezando todos os atritos e considerando a bola como um ponto material, é correto afirmar que a componente
A) horizontal do seu vetor velocidade não muda ao longo da trajetória.
B) vertical do seu vetor velocidade não muda ao longo da trajetória.
C) horizontal do seu vetor aceleração muda ao longo da trajetória.
D) vertical do seu vetor aceleração muda ao longo da trajetória.
Resposta: Do enunciado, é possível perceber que o chute se trata de um lançamento oblíquo e, portanto, é uma composição de dois movimentos, um movimento uniforme na horizontal e um movimento uniformemente variado na vertical. Com isso, a componente horizontal da aceleração e da velocidade são constantes, a primeira sendo igual a zero, enquanto a componente vertical da aceleração é constante diferente de zero e a componente vertical da velocidade muda ao longo da trajetória.
Alternativa correta: A.
+ Veja também: 15 fórmulas de Física para o Enem e vestibulares
Se prepare para o vestibular com o Estratégia!
Nos cursos preparatórios da Coruja, os alunos são preparados para observar as matérias de maneira abrangente, conectando informações de diferentes áreas e consolidando esses dados em simulados e nas provas. Tudo isso é fornecido por meio de aulas ministradas por professores especialistas, além de acesso a materiais didáticos disponíveis em diversos formatos (PDF, vídeo, áudio e etc) Clique no banner e estude Estratégia Vestibulares!




