A aritmética é o ramo da matemática que estuda as operações numéricas desde suas formas mais simples, como soma, subtração, divisão e multiplicação. A origem da palavra remete à “ciência dos números”.
Acompanhe a seguir um resumo sobre aritmética, desde suas operações básicas, com suas definições, regras importantes de priorização entre as 4 operações e outras informações necessárias para o vestibular.
Neste artigo você encontrará, também, a resolução de exercícios que parte do conhecimento aritmético básico para desenvolverem o raciocínio lógico.
Navegue pelo conteúdo
Números e valores posicionais na aritmética
Os números são maneiras simbólicas e matemáticas de representar valores. No sistema decimal de numeração, com apenas 10 algarismos (1,2,3,4,5,7,8,9,0) é possível escrever infinitos valores.
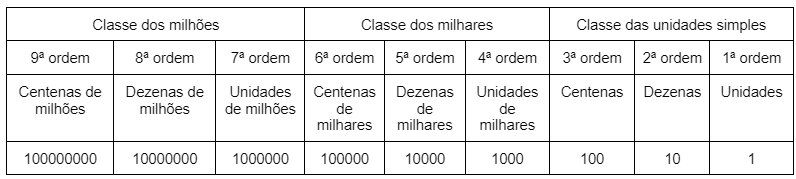
Isso é possibilitado pelo conceito de valor posicional. O número 1, posicionado nas unidades, vale um. Se ele estiver na “casinha” das dezenas, vale 10. Na casa dos milhares, valerá 1000 e assim sucessivamente. Veja uma tabela de sumário:
Conjuntos numéricos
Os conjuntos numéricos são formas de organizar os números conforme suas características, seja pelo fato de serem positivos ou negativos, pela sua capacidade de ser dividido ou não, entre outros tópicos. Veja os principais na listagem a seguir.
- Conjunto dos números naturais: lN = {0,1,2,3,4,5…}, como a contagem que aprendemos na alfabetização primária;
- Números inteiros Z = {-3,-2,-1,0,1,2,3,4…}, possui os números naturais e também os valores negativos;
- Os elementos do conjunto dos números racionais possuem a propriedade de divisão, podem ser fracionários e/ou dízimas periódicas — Q = {…-1,- 1⁄2, 0,+½,+1,+3/2…};
- Os números irracionais são aqueles que formam dízimas não periódicas, raízes não exatas (√5 e √7) e o valor de pi (?), por exemplo; e
- Os números reais agrupam todos os valores citados acima, sendo um conjunto genérico — de forma que entre um número real e outro podem ser contados infinitos valores.
A imagem abaixo tem um diagrama que demonstra a relação entre os conjuntos numéricos, na forma como um está contido no outro.
+ Veja mais: Equação irracional: o que é e como resolver
Intervalos reais: o que são e como representar
Operações básicas de aritmética
As operações básicas da aritmética são soma, subtração, divisão e multiplicação. A partir desses cálculos é possível desenvolver diversas expressões matemáticas úteis para o cotidiano.
No momento das compras, por exemplo, a adição dos valores é a principal ferramenta matemática utilizada. Quando dois itens iguais são comprados, você pode multiplicar o preço da unidade e encontrar o valor gasto naquela aquisição.
No dia a dia, a divisão pode estar presente num passeio com os amigos, quando a conta é dividida entre todos. Nesse caso, é necessário pegar o valor total e fazer com que a soma da parcela de todos os colegas resulte nele. A subtração, então, seria o quanto ainda se deve ao restaurante depois que 3 dos 5 amigos pagaram suas partes.
Soma
Como já foi citado anteriormente e é de conhecimento geral, a soma ou adição trabalha com a acumulação dos valores. Ela possui algumas propriedades especiais que estão listadas abaixo:
- Elas são comutativas, ou seja, a ordem das parcelas não altera o valor final (5 + 8 = 8 + 5);
- Também apresentam propriedades associativas, quando existem três ou mais parcelas, qualquer ordem também não altera o resultado (5 + 8 + 7 = 8 + 7 + 5);
- Existe um elemento neutro (0) que não muda os resultados, independentemente de onde ele se encontra na soma (15 + 0 = 15); e
- A adição permite a existência de um elemento oposto. Valores opostos, quando somados, resultam em 0 — (12 + (-12) = 0).
Subtração
A subtração fornece a diferença de valores entre dois números. Eles são chamados de minuendo (de quem está sendo subtraído) e subtraendo (o que está sendo subtraído).
No exemplo 10 – 7 = 3, temos que 10 é o minuendo, 7 é o subtraendo e 3 é a diferença ou resto encontrado na subtração dos dois valores.
Algumas propriedades dessa operação aritmética estão listadas abaixo
- A subtração não possui elemento neutro porque apresenta resultados divergentes dependendo da posição do zero
4 – 0 = 0
0 – 4 = -4; - A subtração de dois números do mesmo conjunto numérico não necessariamente resultado em um valor dentro daquele mesmo conjunto
40 – 57 = – 17
40 e 57 são naturais e -17 é um valor inteiro; e
- A distribuição associativa de três ou mais parcelas não pode ser aplicada à subtração
100 – 30 – 25 = 65
100 – (30 – 25) = 100 – (- 5) = 105.
Multiplicação
A operação aritmética de multiplicação é aquela que fornece o resultado da soma de um número muitas vezes. De forma que 4 + 4 + 4 + 4+ 4 + 4 é igual a somar seis vezes o número quatro, ou seja: 4 + 4 + 4 + 4+ 4 + 4 = 4 x 6.
Uma das propriedades mais marcantes da multiplicação é que ela é comutativa e associativa, de forma que alterar a ordem dos fatores multiplicativos não altera o resultado final. Seja a expressão numérica de dois ou mais termos. O elemento neutro da multiplicação é 1, porque qualquer número multiplicado por 1 é igual a ele mesmo. A imagem abaixo aborda também a propriedade distributiva dessa operação.
Divisão
A divisão é a operação inversa à multiplicação. Dessa forma, ela trata sobre “em quantas partes iguais é possível separar esse valor?” Veja, a seguir, as principais propriedades das divisões:
- Elas não são uma ferramenta aritmética comutativa. Assim, 6/2 ≠ 2/6;
- Não possuem características associativas 20 ÷ (5 ÷ 2) ≠ (20 ÷ 5) ÷ 2;
- Não existe divisão por 0, ou seja x ÷ 0 = ∄;
- Se o dividendo for igual a 0, a resposta da divisão sempre zero — 0 ÷ x = 0; e
- Todo número dividido por 1 é igual a ele mesmo, como um elemento neutro, como em x ÷ 1 = x.
Jogos de sinais na aritmética
Os jogos de sinais dizem respeito a forma como números inteiros positivos e negativos interagem entre si em uma operação aritmética. Eles podem ser utilizados em todas as operações básicas já citadas, veja um resumo na tabela abaixo.
| Soma | Subtração | Multiplicação | Divisão | |
| + com +(sinais iguais) | 10 + 20 = 30resultado positivo | 30 – (+35) = -5 resultado negativo se o primeiro termo for menor que o segundo 35 – (+30) = 5 resultado positivo se o primeiro termo for maior que o segundo | 5 x 5 = 25 resultado positivo | 20 ÷ 5 = 4 resultado positivo |
| – com -(sinais iguais) | – 10 + (- 20) = – 30- 10 – 20 = -30resultado negativo | – 30 – (-35) = 5- 30 + 35 = 5 resultado positivo se o primeiro termo for maior que o primeiro – 35 – (-30) = -5- 35 + 30 = -5 resultado negativo se o primeiro termo for menor que o primeiro | (-5) x (-5) = 25 resultado positivo | (-20) ÷ (-5) = 4 resultado positivo |
| + com – (sinais diferentes) | 10 + (- 20) = -10 10 – 20 = -10 resultado negativo se o primeiro termo for menor que o segundo 10 + (-3) = 7 10 – 3 = 7 resultado positivo se o primeiro termo for maior que o segundo | 10 – (+ 20) = -10 10 – 20 = -10 resultado negativo se o primeiro termo for menor que o segundo 10 – (+3) = 7 10 – 3 = 7 resultado positivo se o primeiro termo for maior que o segundo | (-5) x 5 = -255 x (-5) = -25 resultado negativo | 20 ÷ (-5) = – 4(-20) ÷ (5) = -4 resultado negativo |
Priorização das operações aritméticas
Uma expressão algébrica pode possuir cálculos aditivos, subtrativos, multiplicativos ou divisivos. A priorização das operações fornece uma série de regras que devem ser seguidas para saber por onde começar as contas.
Diferentemente dos padrões de leitura normal, da esquerda para a direita, a matemática segue outros princípios.
- A multiplicação e a divisão devem ser feitas em primeiro lugar, na ordem em que aparecem;
- Se houverem parênteses, eles precisam ser resolvidos primeiro;
- Depois dos parênteses, as operações em colchetes devem ser concluídas;
- As chaves são os últimos símbolos priorizados nessa lista.
Lembre-se: apesar de dar prioridade às expressões dentro desses símbolos, a multiplicação e a divisão dentro deles também deve acontecer primeiro. Veja a resolução do exercício abaixo para elucidar melhor:
Instituto Federal do Alagoas (IFAL) — 2017
Determine o valor de (33 + 52) ÷ 22.
a) 13
b) 14
c) 15
d) 16
e) 17
Como aprendemos, os parênteses devem ser resolvidos primeiro. No caso da expressão mostrada, as exponenciações foram calculadas e depois os cálculos prosseguiram:
(33 + 52) ÷ 22 = 13
(27 + 25) ÷ 4 = 13
(52) ÷ 4 = 13, como mostra a alternativa A.
Esse outro exercício, também do IFAL, é mais complexo e está resolvido a seguir:
IFAL 2012
A= 3-{-2+[ +3:60+42-(3.4-2)-1]+4} Assinale a alternativa que corresponde ao dobro de A.
a) -7
b) -21
c) 49
d) 14
e) -14
A primeira coisa a se fazer é a resolução dos parênteses:
A = 3-{-2+[ +3:60+42–(3.4-2)-1]+4}
Como o parêntese tem multiplicação, ela deve ser a primeira a ser destrinchada. E depois a subtração:
A = 3- {-2+[ +3:60+42–(3.4-2)-1]+4}
A = 3-{-2+[ +3:60+42–(12-2)-1]+4}
A = 3-{-2+[ +3:60+42–(10)-1]+4}
A = 3-{-2+[ +3:60+42– 10 -1]+4}
Agora que o parêntese já está o menor possível, vamos resolver o colchete, priorizando as exponenciações e divisões, da esquerda para a direita:
A = 3-{-2+[ +3:60+42– 10 -1]+4}
Como todo número elevado a zero é igual a 1, 60=1, então:
A = 3-{-2+[ +3:1+42– 10 -1]+4}
Todo número dividido por 1 é igual a ele mesmo, de forma que 3:1=3
A = 3-{-2+[ +3:1 +42– 10 -1]+4}
A = 3-{-2+[ +3 +42– 10 -1]+4}
A partir de então, resolve-se 42 = 16 e dá-se sequência na operação:
A = 3-{-2+[ +3 +42– 10 -1]+4}
A = 3-{-2+[ +3 +16 – 10 -1]+4}
A = 3-{-2+[ 19 – 10 -1]+4}
A = 3-{-2+[ 9 -1]+4}
A = 3-{-2+[ 8]+4}
A = 3-{-2+8 +4}
Já resolvidos os parênteses e colchetes, devemos iniciar agora a resolução das chaves, com o mesmo sistema de priorização já observados:
A = 3-{-2+8 +4}
A = 3-{6 +4}
A = 3-{10}
A = 3 – 10
A = -7
O dobro de A, que é a informação pedida no enunciado é dado por:
A.2 = -7.2
A.2 = -14, como mostra a alternativa E.
+ Veja também: Equações: principais tipos, fórmulas e aplicações
Progressões aritméticas e geométricas: o que são, como calcular e questões
Questão de aritmética no Enem
ENEM 2014
O criador de uma espécie de peixe tem sete tanques, sendo que cada tanque contém 14 600 litros de água. Nesses tanques, existem em média cinco peixes para cada metro cúbico (m3) de água. Sabe-se que cada peixe consome 1 litro de ração por semana. O criador quer construir um silo que armazenará a ração para alimentar sua criação.
Qual é a capacidade mínima do silo, em litros, para armazenar a quantidade de ração que garantirá a alimentação semanal dos peixes?
a) 511
b) 5 110
c) 51 100
d) 511 000
e) 5 110 000
A questão acima pode ser resolvida apenas com operações aritméticas simples e conhecimento de geometria espacial, veja:
7 tanques de 14600 litros → 7 * 14600 = 102200 litros
Como 1 m3 = 1000 litros, podemos dizer que:
102.200 litros / 1000 = 102,2 m3 de água
Se cada metro cúbico possui 5 peixes, podemos fazer a multiplicação entre essas duas grandezas:
102,2 * 5 = 511 litros de ração é a capacidade mínima do silo a ser construído, como aponta a alternativa A.
Estude mais matemática com o Estratégia Vestibulares!
Nos cursos do Enem do Estratégia você terá o suporte necessário para estudar assuntos essenciais até o dia do Enem. Os temas mais cobrados, como raciocínio lógico, funções de 1º e 2º grau, interpretação gráfica e trigonometria são desenvolvidos com clareza e abordados nos materiais didáticos, que podem ser lidos digitalmente. Quer conhecer melhor? Clique no banner abaixo.




