A probabilidade da intersecção é uma das formas de interpretar dados e informações estatísticas, conhecimento norteia a escolha de diversos profissionais no dia a dia, seja para avaliar a possibilidade de eventos meteorológicos, encaminhar estratégias de compra e venda para aumentar a rentabilidade de uma empresa ou ainda para definir a melhor conduta de tratamento para as condições específicas de cada paciente em um hospital.
Neste artigo, você conhecerá a definição da probabilidade de intersecção, os princípios que embasam esse tipo de cálculo, além de observar exemplos de como é o enunciado típico para questões desse assunto nos vestibulares. Ao final, você verá um passo a passo de como resolver esse cálculo probabilístico.
Navegue pelo conteúdo
O que é a probabilidade da intersecção?
Em matemática, probabilidade é a entidade que permite calcular a chance de um evento B ocorrer, dado um conjunto de A eventos possíveis, de forma que A é chamado de espaço amostral. Esse valor varia de 0 a 1, de forma que 0 significa que existe 0% de B ocorrer e 1 indica que B ocorrerá em 100% das vezes.
No caso da probabilidade da intersecção, avalia-se a possibilidade de dois eventos ocorrerem simultaneamente ou sucessivamente. Sejam os eventos C e D, no espaço amostra S. A probabilidade da intersecção calcula a chance de ocorrer C e D, ao mesmo tempo ou um após o outro.
O que é intersecção?
Para facilitar a interpretação desse tipo de cálculo, é importante se lembrar dos conjuntos de números e as operações que podem ser realizadas com eles. Em matemática, um conjunto numérico é composto por diversos elementos, geralmente descritos sequencialmente, em ordem crescente ou decrescente, como está representado a seguir:
A = {5,8,13,17,22,35,41}
Quando tomamos dois conjuntos aleatórios, pode ser que eles tenham elementos em comum, como no exemplo abaixo:
A = {5,8,13,17,22,35,41}
B = {5,12,15,17,30,41,50,57}
No estudo dos conjuntos numéricos, é comum utilizar uma representação chamada Diagrama de Venn. Nesse esquema, os grupos de números são representados por um círculo e, quando existem elementos em comum, eles ficam agrupados na região compartilhada entre as duas formas geométricas, veja na imagem:
Todo o círculo azul representa os elementos presentes em A, assim como o círculo rosa indica os elementos de B. A zona roxa representa os elementos que estão presentes em A e B ao mesmo tempo, é chamada de intersecção e simbolizada por A ∩ B.
Cálculos probabilidade da intersecção
A probabilidade da intersecção deve ser calculada da seguinte forma:
Considera-se que A e B são dois eventos e S é o espaço amostral
P (A ∩ B) = P (B|A) x P (A) = P (A|B) x P (B)
- P (A ∩ B) é a probabilidade de acontecerem A e B simultânea ou sucessivamente;
- P (B|A) é a probabilidade de B acontecer, considerando que A vai ocorrer;
- P (A|B) é a probabilidade de A acontecer, na condição de que B com certeza ocorrerá;
- P (A) representa a probabilidade do evento A acontecer isoladamente no espaço amostral; e
- P (B) é a probabilidade de B ocorrer independentemente no espaço amostral.
Observe que a fórmula abrange probabilidades condicionais, como P (B|A). Isso é necessário porque, algumas vezes, os eventos não são independentes. Por exemplo, considere que a meteorologia apontou que, se chovesse em um dia qualquer, a chance de chover no dia seguinte é 2 vezes menor do que se não chover no dia anterior.
Se considerarmos que A é a chance de chover no dia 29 de outubro e B é a chance de chover no dia 30 de outubro, há influência de um evento sobre o outro. Afinal, se chover no dia 29 de outubro, a chance de chuva no dia 30 será completamente diferente e essa é a principal razão de abranger probabilidade condicional no cálculo da probabilidade de intersecção.
Quando os eventos não sofrem influência entre si, são chamados de eventos independentes. Nesses casos, a probabilidade condicional não precisa aparecer na fórmula e o cálculo fica simplificado para:
P (A ∩ B) = P (A) x P (B)
Como resolver a probabilidade da intersecção?
Acompanhe o passo a passo da resolução do seguinte enunciado: Em um jogo, é lançado um dado de 6 lados, numerados de 1 a 6. O jogador que conseguir, em dois lançamentos sucessivos, um número ímpar e o número 6 pode efetuar uma manipulação do tabuleiro a seu favor. Pedro está jogando e quer saber qual a probabilidade de manipular o jogo, calcule.
O primeiro passo é identificar o tipo de probabilidade requerida pelo problema. Observe que os eventos são representados por “número ímpar e número 6”. Sempre que a conjunção “e” aparecer em um problema probabilístico, isso se refere à intersecção de dois eventos, geralmente associado a um cálculo de multiplicação.
Agora, devemos avaliar se são dois eventos condicionais ou independentes. Note que o número que Pedro obteve no primeiro lançamento não interfere no valor que aparecerá no segundo lançamento. Isso significa que os eventos são independentes entre si. Então, a fórmula utilizada será P (A ∩ B) = P (A) x P (B). De forma que A = chance de ser um número ímpar e B = chance de ser o número 6.
Para realizar esses cálculos deve-se levar em consideração que o espaço amostral S do lançamento de dados é composto pelos valores S = {1,2,3,4,5,6}, então o número de resultados possíveis é n(S)=6. Os números ímpares desse espaço são 1, 3 e 5, ou seja, n(A) = 3. Enquanto que o evento B é representado pelo número 6, n(B)=1.
Calcula-se a probabilidade de Pedro encontrar um número ímpar em uma de suas jogadas:
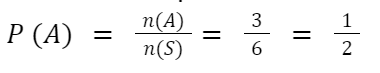
Depois, avalia-se a chance das jogadas apresentarem o número 6, como pede o enunciado:
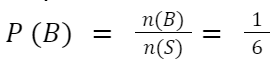
Agora, basta realizar a probabilidade da intersecção, ou seja, de Pedro obter um número ímpar e um número 6 em duas jogadas independentes:
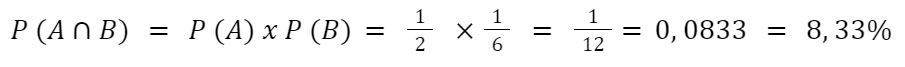
+ Veja também: Probabilidade condicional: o que é, fórmulas e questões de prova
Fórmulas matemáticas: principais fórmulas que aparecem no vestibular
Estude mais com a Coruja!
O Estratégia Vestibulares é uma plataforma de estudo com milhares de questões de vestibulares respondidas de todo o País: o Banco de Questões abrange todas as disciplinas, com resolução de professores especialistas e muitos vídeos explicativos.
Nos cursos preparatórios da Coruja, você terá acesso a aulas específicas, de acordo com o conteúdo programático de cada disciplina, com material didático de qualidade, em diferentes plataformas multimídias. Clique no banner abaixo e saiba mais!