O estudo estatístico e probabilístico possui uma importância sem precedentes em diversas áreas do conhecimento, tanto para avaliar a possibilidade de acontecerem dois eventos exclusivos ao mesmo tempo, como para mensurar suas consequências em diferentes contextos, como evolução de uma doença, relação entre fenômenos climáticos, entre outros exemplos.
Como estudar matemática do ponto de vista probabilístico tem uma aplicação prática específica, muitas provas de vestibulares consideram esse tema como essencial para a entrada na graduação e, para te ajudar a estudar o tema, o Estratégia Vestibulares preparou este artigo com explicações didáticas sobre a probabilidade da união de dois eventos, como interpretar e solucionar problemas com esse tema.
Navegue pelo conteúdo
Definição de probabilidade da união
União de conjuntos números
Ao estudar probabilidade, um conhecimento essencial são os conjuntos numéricos e suas relações. Em matemática, diferentes números podem ser agrupados em conjuntos, que são representados por uma letra maiúscula e cada valor ali presente é chamado de elemento. Como exemplo, veja o conjunto A, com 7 elementos diferentes:
A = {5,9,11,19,27,30,31}
Geralmente, são descritos em forma crescente ou decrescente dos valores, o que é chamado de “organização em rol”. Diferentes conjuntos numéricos podem sofrer operações, que são união, interseção ou diferença.
Em se tratando da união entre dois conjuntos, é representada pelo símbolo ∪, e significa a junção de todos os elementos dos grupos em questão. Tomemos como exemplo um outro grupo numérico B = {14,17,19,23,30,31,35}.
A união entre A e B será:
A ∪ B = (A) + (B)
A ∪ B = (5,9,11,19,27,30,31) + (14,17,19,23,30,31, 35)
A ∪ B = (5,9,11,14,17,19,23,27,30,31,35)
Para facilitar o entendimento, utiliza-se uma ilustração chamada de Diagrama de Venn. Os conjuntos possuem elementos iguais entre si, que são 19, 30 e 31. Na união dos conjuntos eles estarão presentes, assim como todos os outros números que formam A e B.
Probabilidade da união
No caso da probabilidade da união, estamos avaliando a possibilidade do evento A acontecer ou do evento B acontecer. Para isso, a fórmula é construída com soma de probabilidades:
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
Ou seja, a probabilidade da união entre A e B é dada pela probabilidade de acontecer o evento A, mais a probabilidade de acontecer o evento B, subtraída pela probabilidade da intersecção (∩) entre os dois conjuntos.
Lembre-se que a intersecção entre dois conjuntos é representada pelos elementos iguais que possuem. Seja A = {1,5,7,12} e B = {5,12,19,26}, a intersecção A ∩ B = {5,12}. Em alguns casos, os conjuntos não possuem uma intersecção, isto é, não tem nenhum elemento em comum: são eventos mutuamente exclusivos.
Um exemplo seria a probabilidade da união entre C = {99,125,185,202} e D = {112,145,172,326}. Note que nenhum dos elementos é compartilhado por C e D, então são eventos mutuamente exclusivos, de forma que P(C ∩ D) = 0. Então a fórmula será:
P(C ∪ D) = P(C) + P(D) – P(C ∩ D)
P(C ∪ D) = P(C) + P(D) – 0
P(C ∪ D) = P(C) + P(D)
Como resolver probabilidade da união?
Observe que o cálculo da probabilidade da união leva em consideração outras três probabilidades, que devem ser encontradas previamente para chegar ao resultado. Então, vamos partir do seguinte enunciado:
A escola Chocolate Branco está completando 15 anos de existência e decidiram presentear um dos melhores alunos com um tablet para ajudar nos estudos. Para ganhar o sorteio, o estudante deve retirar bolinhas de uma urna, que estão numeradas de 1 a 25. Sempre que o aluno não tira a bola vencedora, ela deve voltar para a urna.
Para ganhar, o número retirado deve ser divisível por 3 ou por 4. João está entre os estudantes escolhidos para a premiação e quer saber qual a probabilidade de ele ganhar. Calcule esse valor.
- O primeiro evento analisado (A) é o número ser divisível por 3;
- O segundo evento (B) delimitado é que o número seja divisível por 4.
Então, a probabilidade uma ou outra acontecer deve ser calculada com a fórmula da probabilidade da união:
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
Antes de iniciarmos, lembre-se que o cálculo de probabilidade leva em conta o número de elementos que se enquadram nos critérios, dividido pelo espaço amostral, que é o número total de eventos.
Probabilidade = evento escolhido / todos os eventos possíveis
- A partir disso, vamos calcular a probabilidade do número ser divisível por 3:

Entre 1 e 25, os números divisíveis por 3 são 3, 6, 9, 12, 15, 18, 21, 24.
n(A) = 8
A caixa possui 25 bolinhas, então:
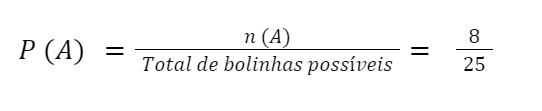
- Agora, vamos calcular a probabilidade do número ser divisível por 4:
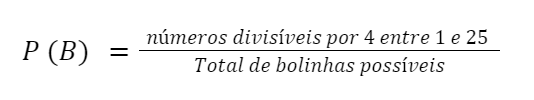
Entre 1 e 25, os números divisíveis por 4 são 4, 8, 12, 16, 20 e 24.
n(B) = 6
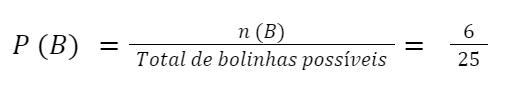
- O próximo passo é calcular a intersecção entre os eventos A e B, ou seja, os números que são divisíveis por 3 e 4 ao mesmo tempo.

O conjunto A = {3, 6, 9, 12, 15, 18, 21, 24} e B = { 4, 8, 12, 16, 20, 24}
Os elementos iguais entre eles estão destacados, totalizando n(A ∩ B) = 2
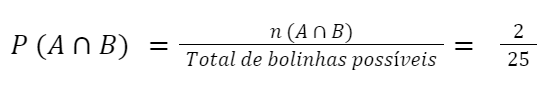
- Por fim, basta adicionar os valores na fórmula inicial:
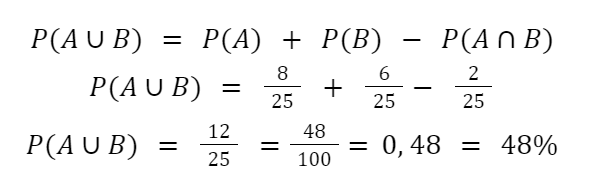
+ Veja também: Probabilidade no Enem: conceitos e como calcular
Probabilidade condicional: o que é, fórmulas e questões de prova
Estude para o vestibular com o Estratégia!
Gostou do conteúdo? Tenha acesso a diversos resumos e explicações didáticas sobre assuntos de Biologia, Geografia, História, Filosofia, Matemática, Física, Química, Português e todas as outras disciplinas. Tudo isso está disponível nos cursos da Coruja, em PDFs ou aulas. Conheça mais: clique no banner abaixo!



