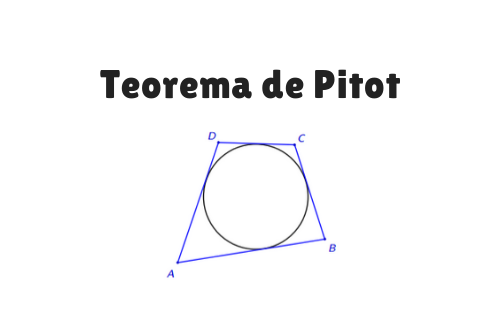
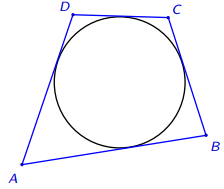
O o teorema de Pitot diz que um quadrilátero convexo ABCD é circunscritível se, e somente se, a soma dos lados opostos é a mesma, AB+CD=AD+BC.
Navegue pelo conteúdo
Demonstração e Curiosidades sobre o teorema de Pitot
A demonstração do teorema decorre da propriedade de segumentos tangentes a uma circunferência:
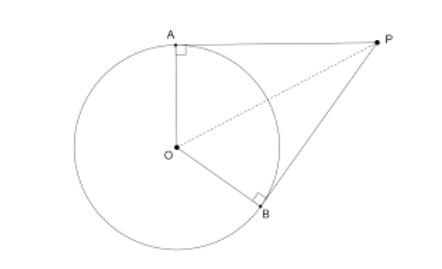
Temos que, como PA e PB tangenciam a circunferência, PA=PB. Isso pode ser provado utilizando congruência de triângulos: , pois
Raio da Circunferência, compartilham o lado PO e são triângulos retângulos.
Ao analisar um quadrilátero circunscritível, vemos que podemos utilizar essa propriedade diversas vezes. Com isso, obtemos:
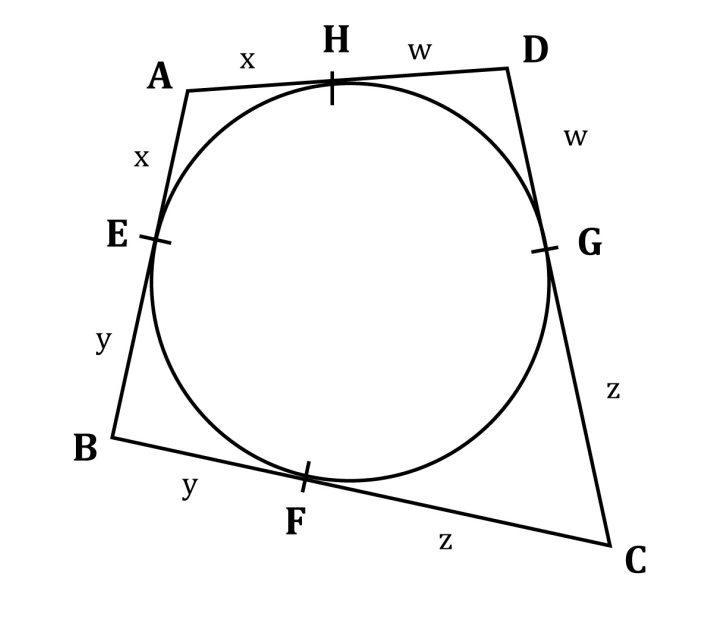
AH=AE=x, EB=BF=y, FC=CG=z, GD=DH=w.
Assim, AD+BC=x+w+y+z e AB+DC=x+y+w+z. Então, vemos que AD+BC=AB+CD. O teorema de Pitot recebeu esse nome em homenagem a Henri Pitot, engenheiro francês responsável por diversos estudos na área de hidrodinâmica.
Também em sua homenagem, foram nomeados os tubos de Pipot, dispositivos que podem ser usados para medir a velocidade de escoamento de um fluido. Esses dispositivos são usados até hoje em aviões, para medir a velocidade do avião em relação ao vento.

Como é cobrado em prova?
Questão ITA 2015
Num triângulo PQR, considere os pontos M e N pertencentes aos lados P Q e P R, respectivamente, tais que o segmento MN seja tangente à circunferência inscrita ao triângulo P QR. Sabendo-se que o perímetro do triângulo PQR é 25 e que a medida de QR é 10, então o perímetro do triângulo PMN é igual a:
a) 5
b) 6
c) 8
d) 10
e) 15
Resolução Comentada
Utilizando as informações fornecidas, podemos construir a seguinte figura:
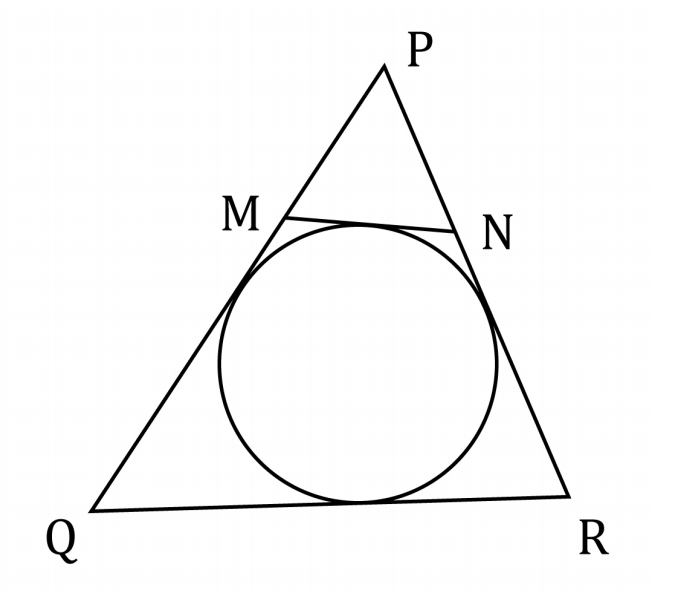
Queremos o perímetro do triângulo PMN, logo queremos a soma s=PM+MN+NP. O quadrilátero MNRQ é circunscritível, então podemos aplicar nele o teorema de Pitot:
MN + QR = MQ + NR. Somando PM+PN em ambos os lados da igualdade, obtemos:
PM+PN+MN+QR=PM+PN+MQ+NR (*).
Do lado esquerdo da igualdade, temos exatamente a soma s desejada, mais QR. Do lado direito, temos PM+MQ+PN+NR.
Mas PM+MQ=PQ e PN+NR=PR, e sabemos que PQ+PR+QR=25.
Como foi dado que QR=10, PQ+PR=15. Substituindo todas essas informações na expressão (*), chegamos em:
s+QR=15 → s+10=15 → s=5
Veja também:
- Geometria: o que é e como é classificada
- Figuras Geométricas: planas, espaciais e como aparece nos vestibulares
- Geometria Plana no Enem: conceito e definições
- Semelhança de triângulos
- Círculo e circunferência: conceitos e exercícios
- Geometria analítica: fórmulas, gráficos e equações
- Geometria Espacial: conheça os sólidos e fórmulas
- Área do trapézio: conheça a fórmula e como calcular!
- Prova FUVEST 2020 – Matemática – Resolução Comentada
- Resolução da prova de Matemática da 2ª Fase da Unicamp 2020
- Prova UNESP 2020 – Matemática – Resolução Comentada