O gráfico de função é uma das formas de representar equações matemáticas. Por meio dele é possível entender o padrão de crescimento ou decaimento de uma grandeza ao longo do tempo, com utilidade em diversas áreas.
As pesquisas científicas utilizam estatísticas para entender o resultado de uma hipótese. Geralmente, esses dados podem ser compilados em gráficos e o desenho apresentado demonstra a qual função está associado padrão observado. Assim, as conclusões podem ser mais precisas e é possível, até mesmo, prever valores futuros.
Diante da importância da construção e interpretação dos gráficos, a maior parte dos vestibulares nacionais costuma cobrar esse assunto de forma intertextual: com conceitos matemáticos alinhados com outras disciplinas.
Para se preparar, leia este artigo da Coruja, que aborda os gráficos de função e como você pode construí-los com facilidade. Além disso, veja descrições gráficas, que permitem compreender padrões observados em diferentes tipos de equações. Vamos lá?
Navegue pelo conteúdo
Como fazer um gráfico de função?
O gráfico de uma função representa um reflexo de como essa função é, é uma forma de expressar o comportamento dessa função a depender do valor que é adicionado nela. Inclusive, é necessário relembrar que uma equação funcional pode ser entendida como uma máquina que transforma um número x em um número y.
Em geral, cada tipo de função terá um padrão específico de gráfico. Isso permite que vejamos um traçado e determinar qual tipo de lei de formação construiu aquela representação. Então, esse conhecimento pode ser importante para saber o que esperar graficamente quando encontrar uma equação ou para determinar uma classificação de função para determinado desenho gráfico.
Para construir os gráficos, foi determinado um ambiente matemático apropriado, que é chamado de plano cartesiano. Trata-se de uma região que tem como parâmetro dois eixos: horizontal, chamado de abscissas (x); e o vertical, chamado de ordenadas (y).
As retas que determinam os eixos são infinitas e a cada unidade de distância aumenta-se o valor de x para a direita, e de y para cima. A partir disso, é possível determinar pontos no gráfico para cada valor de x e y.
Nesse sentido, uma função que transforma x em y pode ser representada da seguinte forma: escolhe-se um valor de x e substitui-o no cálculo matemático. O resultado será o valor de y. Então, o primeiro ponto cartesiano terá as coordenadas P (x,y): fica na direção do valor de x e do valor de y. Ao fazer isso sucessivamente, com diferentes valores x, você encontrará um padrão de desenvolvimento dessa equação, que é o gráfico.
Veja um exemplo com a função f(x) = x + 5, de forma que as coordenadas serão estabelecidas a partir de x + 5 = y. Com essas informações em mãos, vamos adicionar diferentes valores de x e encontrar os respectivos valores de y.
Ponto A, com x = 1
x + 5 = y
1 + 5 = 6
y = 6
A (1,6)
Ponto B, com x = 2
x + 5 = y
2 + 5 = 7
y = 7
B (2,7)
Ponto C, com x = 3
3 + 5 = y
3 + 5 = 8
y = 8
C (3,8)
Ponto D, com x = 4
4 + 5 = y
4 + 5 = 9
y = 9
D (4,9)
Agora basta localizar os valores de abscissas e ordenadas no plano cartesiano, para marcar cada um desses pontos. A partir disso, basta unir os pontos por meio de uma linha contínua, que formará o desenho típico do tipo de função utilizada, que é uma função do primeiro grau.
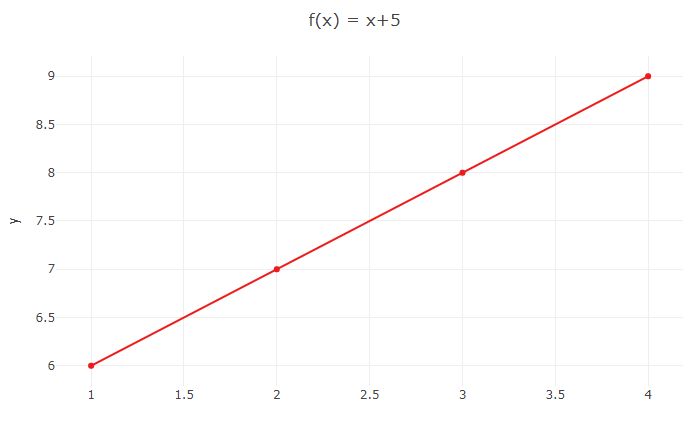
Importante notar que, à medida que o valor de x aumenta, o valor de y também aumenta — isso caracteriza uma função crescente. Já uma função decrescente teria o comportamento inverso, o aumento de x resulta em uma redução dos valores de y.
Esse mesmo princípio deve ser adotado em qualquer outro tipo de função matemática, em que há uma incógnita x e possíveis valores de y. Veja um exemplo, agora, com uma função do segundo grau.
f(x) = x2 + 2
y = x2 + 2
Ponto A, x = 1
y = 12 + 2
y = 1 + 2
y = 3
A (1,3)
Ponto B, x = 3
y = 32 + 2
y = 9 + 2
y = 11
B (3,11)
Ponto C, x = 5
y = 52 + 2
y = 25 + 2
y = 27
C (5,27)
Ponto D, x = 7
y = 72 + 2
y = 49 + 2
y = 51
D (7,51)
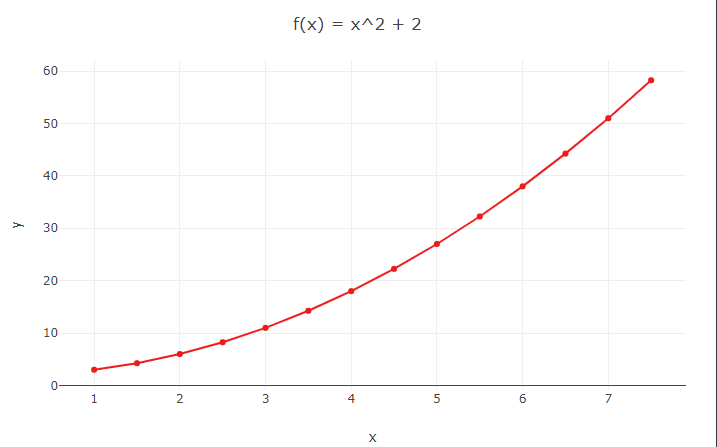
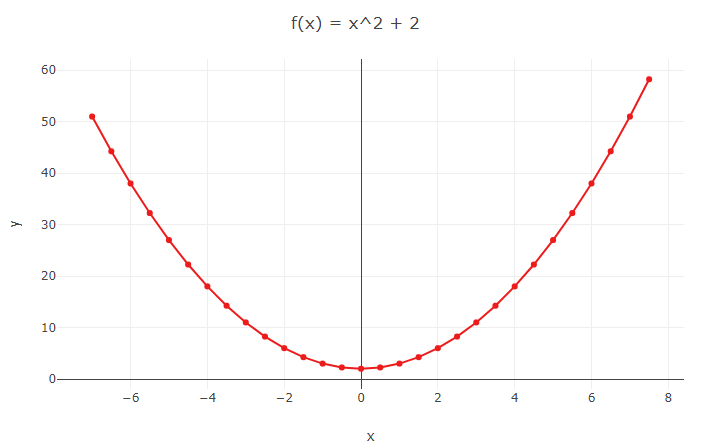
Veja que esse gráfico tem um desenho mais curvo do que o apresentado anteriormente. Para entender exatamente o desenho, seria importante também estabelecer valores negativos de x, para chegar à forma parabólica, que é o padrão típico para funções do segundo grau.
Tipos de gráficos de função
| Tipo de função | Fórmula geral | Gráfico | Formato de gráfico |
| 1º grau | f(x) = ax + b | Reta | |
| 2º grau | f(x) = ax2 + bx + c | Parábola | |
| Exponencial | f(x) = ax | Curva | |
| Logarítmica | f(x) = loga x | Curva | |
| Trigonométrica | f(x) = sen x | Padrão de ondas |
Questões sobre gráfico de função
(Enem PPL 2013) Em um experimento, uma cultura de bactérias tem sua população reduzida pela
metade a cada hora, devido à ação de um agente bactericida. Neste experimento, o número de bactérias em função do tempo pode ser modelado por uma função do tipo
a) afim.
b) seno.
c) cosseno.
d) logarítmica crescente.
e) exponencial.
No início da cultura, vamos imaginar que o número de bactérias seja N e represente o valor de y. Depois, x será representado pelo tempo.
tempo = 0, bac = N
tempo 1, bac = N/2
tempo 2, bac = N/4
tempo 3, bac = N/8
tempo 4, bac = N/16
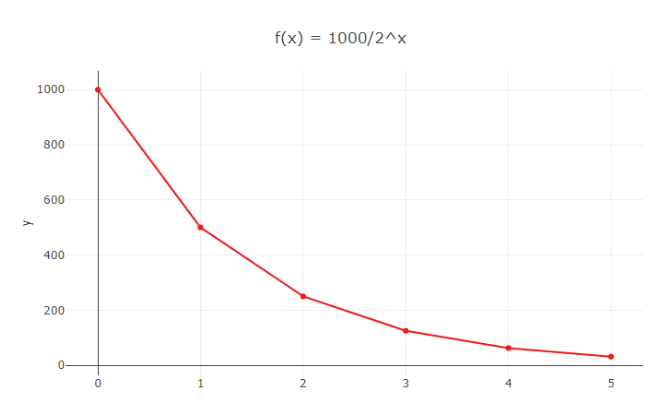
Se formos passar isso para um gráfico, vamos imaginar que N = 1000
x = 0, y = 1000
x = 1, y = 500
x = 2, y = 250
x = 3, y = 125
x = 4, y = 62,5
Esse padrão é clássico de uma função exponencial, como aponta a alternativa E.
Estude com o Estratégia Vestibulares!
Os cursos da Coruja trazem o essencial para te ajudar na jornada rumo à aprovação: as aulas estão disponíveis em vídeos, pdf ou livros digitais. Com isso, o acesso ao conteúdo é facilitado e você pode aprender de onde quiser, além disso, suas anotações ficam salvas e podem ser conferidas durante as revisões. Não perca tempo e saiba mais!




