O sistema de numeração decimal, como sugere o nome, utiliza o número dez para basear todas as operações matemáticas. Isso significa que as contagens são realizadas a partir de unidades de dez, como as dezenas (10), as centenas (102), os milhares (103) e assim sucessivamente.
Acompanhe um resumo sobre as características desse sistema de numeração, que é o mais utilizado no mundo ocidental. Entenda quais são os algarismos envolvidos e como os valores podem ser agrupados, a influência do número zero, entre outras informações!
Navegue pelo conteúdo
Como surgiu o sistema de numeração decimal?
A necessidade de contar, dividir e somar valores, itens, intervalos de tempo e objetos nos remete aos primeiros hominídeos da história evolutiva. Desde os tempos pré-históricos, quando não haviam formas concretas de escrita, os indivíduos utilizavam estratégias que facilitassem a contagem.
Registros paleolíticos de cavernas, ossos, madeiras e pedras podem mostrar isso, como na imagem a seguir:
Acredita-se que com a revolução neolítica, a agricultura rudimentar e a domesticação dos animais, os homens desenvolveram maneiras de controlar os plantios e as cabeças de animais que possuíam.
Inclusive, você sabia que “cálculo” vem de calculus que, em latim significa pedrinha. Isso porque era de costume corresponder uma pedrinha para cada coisa contada. Por exemplo, um pastor de rebanho juntava uma pedra para cada ovelha e guardava-as em uma bolsinha.
Depois, quando fosse novamente tratar do rebanho, repassava a quantidade de pedras — caso houvessem mais pedras que ovelhas, ele provavelmente tinha perdido um de seus animais.
Veja que, de fato, a contagem é uma atividade antiga, mas os sistemas de numeração são mais complexos: representam formas de organizar os valores de maneira padronizada, que pode ser estendido a diferentes populações.
Os primeiros indícios da padronização da contagem surgiu com os elementos egípcios, um povo da Antiguidade Oriental. Eles criaram símbolos representativos e sempre os agrupavam em conjuntos de dez, assim como fazemos atualmente. Veja na imagem abaixo:
Depois, a civilização de Roma foi responsável por atrelar letras aos números e estabelecer um sistema de contagem próprio.
Os números romanos são utilizados até hoje em relógios, estudos científicos e até mesmo no dia a dia, como quando falamos de século V (século 5). Apesar da fácil escrita desses números, ainda parecia muito complexo estabelecer operações matemáticas com eles.
Foi então que os hindus trouxeram uma inovação para a forma de contagem: o número zero. Além de facilitar a representação dos números múltiplos de dez, o zero possibilitou a subtração de um número por ele mesmo, como 1-1=0. Mas só depois que os indianos conseguiram adicionar o zero ao sistema de numeração.
Essa é a história do sistema de numeração decimal hindu arábico, que se concretizou com os símbolos hindus coordenados, com os algarismos: 0,1,2,3,4,5,6,7,8 e 9. Por serem dez algarismos que indicam os infinitos números possíveis na natureza, a nomenclatura “decimal” é utilizada.
Classificações do sistema de numeração decimal
Antes de iniciarmos o estudo das ordens e classes no sistema de numeração decimal, vamos conceituar alguns elementos básicos:
- Número é o valor representado como um todo — é o resultado obtido de uma operação matemática;
- Algarismo, que também pode ser chamado de dígito, é o símbolo matemático básico (0,1,2,3,4,5,6,7,8,9); e
- Numeral é a representação de um número em um determinado sistema numérico. Veja os exemplos.
O número doze pode ser representado pelo numeral 12 no sistema hindu-arábico, em que foram utilizados os algarismos 1 e 2. Ou também com o numeral XII, no sistema romano, com os algarismos X e I.
Ordens e classes
Agora que você já conhece os conceitos fundamentais da contagem no sistema decimal de numeração, é preciso entender que existe uma padronização posicional dos algarismos.
Um mesmo algarismo, em uma posição diferente, representa um valor diferente. Por exemplo, o dígito 1:
- Nas unidades é o valor 1;
- Nas dezenas, marca 10;
- Nas centenas, 100;
- Nos milhares indica o valor de 1000; e assim por diante.
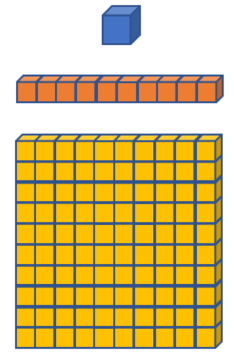
A imagem acima mostra:
- a unidade em azul;
- o conjunto de dez unidades (dezenas) em laranja; e
- o conjunto de dez dezenas (centenas) em amarelo.
Cada classe do sistema decimal possui três ordens possíveis, da seguinte maneira:
- A classe simples (1ª) agrupa unidades, dezenas e centenas;
- A classe dos milhares (2ª) é um conjunto de unidades de milhares, dezenas de milhares e centenas de milhares; e
- A classe dos milhões (3ª) contém unidades de milhões, dezenas de milhões e centenas de milhões. O mesmo padrão se repetirá para bilhões, trilhões, quatrilhões e além.
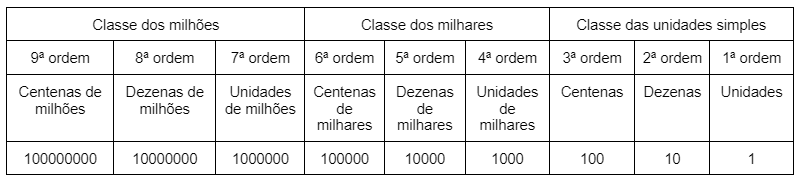
Representações do sistema de numeração decimal
Vamos então destrinchar alguns valores para entender como o sistema de numeração acontece na prática.
Sabemos que o valor 160.723 é cento e sessenta mil, setecentos e vinte e três. Mas, como eles estariam distribuídos em ordens e classes?
- Uma centena de milhares (100.000);
- Seis dezenas de milhares (60.000);
- 0 unidades de milhares (0.000);
- Sete centenas simples (700);
- Duas dezenas simples (20); e
- Três unidades simples (3).
Veja, que, quando somados, esses números resultam exatamente em 160.723.
Para facilitar o processo de decomposição desse número na classificação sistemática, você pode utilizar uma tabela:
| Centenas de milhões | Dezenas de milhões | Unidades de milhões | Centenas de milhares | Dezenas de milhares | Unidades de milhares |
| 1 | 6 | 0 | 7 | 2 | 3 |
Questões sobre sistemas de numeração decimal
ENEM 2014
Os incas desenvolveram uma maneira de registrar quantidades e representar números utilizando um sistema de numeração decimal posicional: um conjunto de cordas com nós denominado quipus. O quipus era feito de uma corda matriz, ou principal (mais grossa que as demais), na qual eram penduradas outras cordas, mais finas, de diferentes tamanhos e cores (cordas pendentes). De acordo com a sua posição, os nós significavam unidades, dezenas, centenas e milhares Na Figura 1, o quipus representa o número decimal 2 453. Para representar o “zero” em qualquer posição, não se coloca nenhum nó.
O número da representação do quipus da Figura 2, em base decimal, é
a) 364.
b) 463.
c) 3.064.
d) 3.640.
e) 4.603.
Na figura 2, temos três quipus na ordem dos milhares (3.000), zero quipus na ordem das centenas, seis quipus nas dezenas (60) e quatro quipus na ordem das unidades (4). Somados, esses valores representam 3000+60+4= 3064.
Veja que o número zero ficou exatamente na ordem das centenas, como demonstra a imagem. Assim, a alternativa correta é a letra C.
Aprenda mais para o Enem com a Coruja!
No curso preparatório Enem do Estratégia Vestibulares, você terá aulas sobre os assuntos mais recorrentes nessa prova, além de ter a oportunidade de sanar suas dúvidas nos materiais e fóruns onlines. Prepare-se com a Coruja! Clique no banner e saiba mais.
Veja também:
- História dos números complexos
- Estatística: princípios, variáveis e como calcular
- Números Irracionais: como provar que um número é irracional?
- Número Pi (π): origem e aplicações!
- Princípio da Indução Finita
- Teorema de Taylor: o que diz e como é cobrado em prova?
- Fórmula de De Moivre: conceito e como é cobrado em prova?
- Axiomas de Peano
- Prova de matemática Fuvest 2020 com Resolução Comentada
- Resolução da prova de Matemática da 2ª Fase da Unicamp 2020
- Prova de Matemática UNESP 2020 com Resolução Comentada




